YOLO-V3代码解析系列（五） —— 损失函数（yolov3.py）

代码结构

1. 构建网络，级联三个尺度的输出（相对于 gridcell）
2. decode：网络输出转换为原图尺度
3. 边界框损失
4. 置信度损失
5. 分类损失

代码展示

import numpy as np
import tensorflow as tf
import core.utils as utils
import core.common as common
import core.backbone as backbone
from core.config import cfg


class YOLOV3(object):
    """Implement tensorflow yolov3 here"""
    def __init__(self, input_data, trainable):
        self.trainable = trainable
        self.classes = utils.read_class_names(cfg.YOLO.CLASSES)
        self.num_class = len(self.classes)
        self.strides = np.array(cfg.YOLO.STRIDES)
        self.anchors = utils.get_anchors(cfg.YOLO.ANCHORS)
        self.anchor_per_scale = cfg.YOLO.ANCHOR_PER_SCALE
        self.iou_loss_thresh = cfg.YOLO.IOU_LOSS_THRESH
        self.upsample_method = cfg.YOLO.UPSAMPLE_METHOD

        try:
        	# 网络输出：3个stride的输出
            self.conv_lbbox, self.conv_mbbox, self.conv_sbbox = self.__build_network(input_data)
        except:
            raise NotImplementedError("Can not build up yolov3 network!")

        # decode：将网络的预测值(相对于grid, 小于1)恢复到原图的尺度下
        with tf.variable_scope('pred_sbbox'):
            self.pred_sbbox = self.decode(self.conv_sbbox, self.anchors[0], self.strides[0])

        with tf.variable_scope('pred_mbbox'):
            self.pred_mbbox = self.decode(self.conv_mbbox, self.anchors[1], self.strides[1])

        with tf.variable_scope('pred_lbbox'):
            self.pred_lbbox = self.decode(self.conv_lbbox, self.anchors[2], self.strides[2])

    def __build_network(self, input_data):
        route_1, route_2, input_data = backbone.darknet53(input_data, self.trainable)

        input_data = common.convolutional(input_data, (1, 1, 1024, 512), self.trainable, 'conv52')
        input_data = common.convolutional(input_data, (3, 3, 512, 1024), self.trainable, 'conv53')
        input_data = common.convolutional(input_data, (1, 1, 1024, 512), self.trainable, 'conv54')
        input_data = common.convolutional(input_data, (3, 3, 512, 1024), self.trainable, 'conv55')
        input_data = common.convolutional(input_data, (1, 1, 1024, 512), self.trainable, 'conv56')

        conv_lobj_branch = common.convolutional(input_data, (3, 3, 512, 1024), self.trainable, name='conv_lobj_branch')
        conv_lbbox = common.convolutional(conv_lobj_branch, (1, 1, 1024, 3 * (self.num_class + 5)),
                                          trainable=self.trainable, name='conv_lbbox', activate=False, bn=False)

        input_data = common.convolutional(input_data, (1, 1, 512, 256), self.trainable, 'conv57')
        input_data = common.upsample(input_data, name='upsample0', method=self.upsample_method)

        with tf.variable_scope('route_1'):
            input_data = tf.concat([input_data, route_2], axis=-1)

        input_data = common.convolutional(input_data, (1, 1, 768, 256), self.trainable, 'conv58')
        input_data = common.convolutional(input_data, (3, 3, 256, 512), self.trainable, 'conv59')
        input_data = common.convolutional(input_data, (1, 1, 512, 256), self.trainable, 'conv60')
        input_data = common.convolutional(input_data, (3, 3, 256, 512), self.trainable, 'conv61')
        input_data = common.convolutional(input_data, (1, 1, 512, 256), self.trainable, 'conv62')

        conv_mobj_branch = common.convolutional(input_data, (3, 3, 256, 512), self.trainable, name='conv_mobj_branch')
        conv_mbbox = common.convolutional(conv_mobj_branch, (1, 1, 512, 3 * (self.num_class + 5)),
                                          trainable=self.trainable, name='conv_mbbox', activate=False, bn=False)

        input_data = common.convolutional(input_data, (1, 1, 256, 128), self.trainable, 'conv63')
        input_data = common.upsample(input_data, name='upsample1', method=self.upsample_method)

        with tf.variable_scope('route_2'):
            input_data = tf.concat([input_data, route_1], axis=-1)

        input_data = common.convolutional(input_data, (1, 1, 384, 128), self.trainable, 'conv64')
        input_data = common.convolutional(input_data, (3, 3, 128, 256), self.trainable, 'conv65')
        input_data = common.convolutional(input_data, (1, 1, 256, 128), self.trainable, 'conv66')
        input_data = common.convolutional(input_data, (3, 3, 128, 256), self.trainable, 'conv67')
        input_data = common.convolutional(input_data, (1, 1, 256, 128), self.trainable, 'conv68')

        conv_sobj_branch = common.convolutional(input_data, (3, 3, 128, 256), self.trainable, name='conv_sobj_branch')
        conv_sbbox = common.convolutional(conv_sobj_branch,
                                          (1, 1, 256, 3 * (self.num_class + 5)),
                                          trainable=self.trainable,
                                          name='conv_sbbox', activate=False, bn=False)
        # print("conv_sbbox: ", conv_sbbox)
        # conv_sbbox: (2, 52, 52, 18) for input 416

        return conv_lbbox, conv_mbbox, conv_sbbox

    def decode(self, conv_output, anchors, stride):
        """
        return tensor of shape [batch_size, output_size, output_size, anchor_per_scale, 5 + num_classes]
               5+num_class: (x, y, w, h, score, probability)
        """

        conv_shape = tf.shape(conv_output)
        batch_size = conv_shape[0]
        output_size = conv_shape[1]
        anchor_per_scale = len(anchors)
        print('anchors[0]: ', anchors)
        # stride=8的anchor
        # [[16.75   19.]
        #  [38.75   42.125]
        #  [95.625  110.125]]

        conv_output = tf.reshape(conv_output,
                                 (batch_size, output_size, output_size, anchor_per_scale, 5 + self.num_class))

        # 原始网络输出的(x, y, w, h, score, probability)
        conv_raw_dxdy = conv_output[:, :, :, :, 0:2]  # 中心位置的偏移量 x,y
        conv_raw_dwdh = conv_output[:, :, :, :, 2:4]  # 预测框长宽的偏移量 w,h
        conv_raw_conf = conv_output[:, :, :, :, 4:5]  # 预测框的置信度 score
        conv_raw_prob = conv_output[:, :, :, :, 5:]   # 预测框类别概率 prob

        # tf.tile:按列数(output_size)扩展input,见下面的例子
        # [[0]    [[0 0 0]
        #  [1]     [1 1 1]
        #  [2]]    [2 2 2]]
        y = tf.tile(tf.range(output_size, dtype=tf.int32)[:, tf.newaxis], [1, output_size])
        # 按行数(output_size)扩展input
        x = tf.tile(tf.range(output_size, dtype=tf.int32)[tf.newaxis, :], [output_size, 1])

        # 构造与输出shape一致的xy_grid,便于将预测的(x,y,w,h)反算到原图
        xy_grid = tf.concat([x[:, :, tf.newaxis], y[:, :, tf.newaxis]], axis=-1)

        xy_grid = tf.tile(xy_grid[tf.newaxis, :, :, tf.newaxis, :], [batch_size, 1, 1, anchor_per_scale, 1])
        xy_grid = tf.cast(xy_grid, tf.float32)  # 计算网格左上角坐标，即Cx,Cy
        print(xy_grid)
        # xy_grid shape
        # (4, 13, 13, 3, 2)
        # 2:存储的是网格的偏移量,类似与遍历网格
        # [[[0. 12.]
        #   [0. 12.]
        #   [0. 12.]]
        #
        # [[1. 12.]
        #  [1. 12.]
        #  [1. 12.]]
        #  ...
        # [[12. 12.]
        #  [12. 12.]
        #  [12. 12.]]]

        # 计算相对于每个grid的
        # tf.sigmoid(conv_raw_dxdy): sigmoid使得值处于[0,1],即相对于grid的偏移
        # 乘以stride: 恢复到最终的输出下的尺度下
        pred_xy = (tf.sigmoid(conv_raw_dxdy) + xy_grid) * stride
        print(pred_xy)
        pred_wh = (tf.exp(conv_raw_dwdh) * anchors) * stride
        pred_xywh = tf.concat([pred_xy, pred_wh], axis=-1)

        # 置信度和分类概率使用sigmoid
        pred_conf = tf.sigmoid(conv_raw_conf)
        pred_prob = tf.sigmoid(conv_raw_prob)

        return tf.concat([pred_xywh, pred_conf, pred_prob], axis=-1)

    def focal(self, target, actual, alpha=1, gamma=2):
        # 目标检测中, 通常正样本较少, alpha可以调节正负样本的比例,
        focal_loss = alpha * tf.pow(tf.abs(target - actual), gamma)
        return focal_loss

    def bbox_giou(self, boxes1, boxes2):
        # boxes:[x,y,w,h]转化为[xmin,ymin,xmax,ymax]
        boxes1 = tf.concat([boxes1[..., :2] - boxes1[..., 2:] * 0.5,
                            boxes1[..., :2] + boxes1[..., 2:] * 0.5], axis=-1)
        boxes2 = tf.concat([boxes2[..., :2] - boxes2[..., 2:] * 0.5,
                            boxes2[..., :2] + boxes2[..., 2:] * 0.5], axis=-1)

        boxes1 = tf.concat([tf.minimum(boxes1[..., :2], boxes1[..., 2:]),
                            tf.maximum(boxes1[..., :2], boxes1[..., 2:])], axis=-1)
        boxes2 = tf.concat([tf.minimum(boxes2[..., :2], boxes2[..., 2:]),
                            tf.maximum(boxes2[..., :2], boxes2[..., 2:])], axis=-1)

        # 计算boxe1和boxes2的面积
        boxes1_area = (boxes1[..., 2] - boxes1[..., 0]) * (boxes1[..., 3] - boxes1[..., 1])
        boxes2_area = (boxes2[..., 2] - boxes2[..., 0]) * (boxes2[..., 3] - boxes2[..., 1])

        # 计算boxe1和boxes2交集的左上角和右下角坐标
        left_up = tf.maximum(boxes1[..., :2], boxes2[..., :2])
        right_down = tf.minimum(boxes1[..., 2:], boxes2[..., 2:])

        # 计算交集区域的宽高, 没有交集,宽高为置0
        inter_section = tf.maximum(right_down - left_up, 0.0)
        inter_area = inter_section[..., 0] * inter_section[..., 1]
        union_area = boxes1_area + boxes2_area - inter_area
        iou = inter_area / union_area

        # 计算最小闭合面C的左上角和右下角坐标
        enclose_left_up = tf.minimum(boxes1[..., :2], boxes2[..., :2])
        enclose_right_down = tf.maximum(boxes1[..., 2:], boxes2[..., 2:])

        # 计算最小闭合面C的宽高
        enclose = tf.maximum(enclose_right_down - enclose_left_up, 0.0)
        enclose_area = enclose[..., 0] * enclose[..., 1]

        # 计算GIOU
        giou = iou - 1.0 * (enclose_area - union_area) / enclose_area

        return giou

    def bbox_iou(self, boxes1, boxes2):
		# 分别计算2个边界框的面积
        boxes1_area = boxes1[..., 2] * boxes1[..., 3]
        boxes2_area = boxes2[..., 2] * boxes2[..., 3]
		
		# (x,y,w,h)->(xmin,ymin,xmax,ymax)
        boxes1 = tf.concat([boxes1[..., :2] - boxes1[..., 2:] * 0.5,
                            boxes1[..., :2] + boxes1[..., 2:] * 0.5], axis=-1)
        boxes2 = tf.concat([boxes2[..., :2] - boxes2[..., 2:] * 0.5,
                            boxes2[..., :2] + boxes2[..., 2:] * 0.5], axis=-1)
		
		# 找到左上角最大的的坐标和右下角最小的坐标
        left_up = tf.maximum(boxes1[..., :2], boxes2[..., :2])
        right_down = tf.minimum(boxes1[..., 2:], boxes2[..., 2:])
		# 判断右下角的坐标是不是大于左上角的坐标，大于则有交集，否则没有交集
        inter_section = tf.maximum(right_down - left_up, 0.0)
        inter_area = inter_section[..., 0] * inter_section[..., 1]
        # 计算并集，并计算IOU
        union_area = boxes1_area + boxes2_area - inter_area
        iou = 1.0 * inter_area / union_area

        return iou

    def loss_layer(self, conv, pred, label, bboxes, anchors, stride):
        # conv: Tensor("define_loss/conv_sbbox/BiasAdd:0", shape=(?, ?, ?, 18)
        # 网络最后的输出层的shape
        conv_shape = tf.shape(conv)
        batch_size = conv_shape[0]
        output_size = conv_shape[1]
        input_size = stride * output_size

        conv = tf.reshape(conv, (batch_size,
                                 output_size,
                                 output_size,
                                 self.anchor_per_scale,
                                 5 + self.num_class))

        print('conv reshape:\n', conv)
        # 网络输出的预测值, shape=(?, ?, ?, 18), 然后被reshape为如下形状：
        # (batch_size, output_size, output_size, anchor_per_scale, 5 + num_class)
        # 尺度相对与grid
        conv_raw_conf = conv[:, :, :, :, 4:5]  # 置信度
        conv_raw_prob = conv[:, :, :, :, 5:]   # 类别概率

        # decode之后的预测坐标和置信度,尺度相对于原图
        pred_xywh = pred[:, :, :, :, 0:4]
        pred_conf = pred[:, :, :, :, 4:5]

        # 标签信息
        label_xywh = label[:, :, :, :, 0:4]
        respond_bbox = label[:, :, :, :, 4:5]  # 置信度,判断网格内有无目标
        label_prob = label[:, :, :, :, 5:]
        print('label_xywh: ', label_xywh)

        giou = tf.expand_dims(self.bbox_giou(pred_xywh, label_xywh), axis=-1)
        input_size = tf.cast(input_size, tf.float32)
        print('inputsize: ', input_size)

        # 2-相对面积
        # bbox_loss_scale: 弱化边界框尺寸对损失值的影响
        # giou权重, [1,2]增加小目标的权重
        bbox_loss_scale = 2.0 - 1.0 * label_xywh[:, :, :, :, 2:3] * label_xywh[:, :, :, :, 3:4] / (input_size ** 2)
        print('bbox_loss_scale: ', bbox_loss_scale)

        # 边界框损失
        giou_loss = respond_bbox * bbox_loss_scale * (1 - giou)

        # 计算预测框与真实框的IOU
        iou = self.bbox_iou(pred_xywh[:, :, :, :, np.newaxis, :], bboxes[:, np.newaxis, np.newaxis, np.newaxis, :, :])
        # 找出与真实框IOU最大的边界框
        max_iou = tf.expand_dims(tf.reduce_max(iou, axis=-1), axis=-1)

        # 如果最大的IOU小于阈值, 那么认为不包含目标,则为背景框
        respond_bgd = (1.0 - respond_bbox) * tf.cast(max_iou < self.iou_loss_thresh, tf.float32)

        # 预测为正样本,计算focal损失：(-1) * alpha * (1-predict)^gamma * log(predict)
        conf_focal = self.focal(respond_bbox, pred_conf)

        # 置信度损失： 如果网格包含物体，则置信度为1，否则为0
        conf_loss = conf_focal * (
                respond_bbox * tf.nn.sigmoid_cross_entropy_with_logits(labels=respond_bbox, logits=conv_raw_conf)
                +
                respond_bgd * tf.nn.sigmoid_cross_entropy_with_logits(labels=respond_bbox, logits=conv_raw_conf)
        )

        # 分类损失：
        prob_loss = respond_bbox * tf.nn.sigmoid_cross_entropy_with_logits(labels=label_prob, logits=conv_raw_prob)

        giou_loss = tf.reduce_mean(tf.reduce_sum(giou_loss, axis=[1, 2, 3, 4]))
        conf_loss = tf.reduce_mean(tf.reduce_sum(conf_loss, axis=[1, 2, 3, 4]))
        prob_loss = tf.reduce_mean(tf.reduce_sum(prob_loss, axis=[1, 2, 3, 4]))

        return giou_loss, conf_loss, prob_loss

    def compute_loss(self, label_sbbox, label_mbbox, label_lbbox, true_sbbox, true_mbbox, true_lbbox):
        # 计算小尺寸目标框的损失函数
        with tf.name_scope('smaller_box_loss'):
            loss_sbbox = self.loss_layer(self.conv_sbbox,  # 网络的直接输出
                                         self.pred_sbbox,  # decode网络的输出,输入图的尺度(416)
                                         label_sbbox,  # 标签,(output_size, output_size, 3, 5+num_class)
                                         true_sbbox,  # 真实框 (150, 4)
                                         anchors=self.anchors[0], stride=self.strides[0])

        # 计算中等尺寸目标框的损失函数
        with tf.name_scope('medium_box_loss'):
            loss_mbbox = self.loss_layer(self.conv_mbbox, self.pred_mbbox, label_mbbox, true_mbbox,
                                         anchors=self.anchors[1], stride=self.strides[1])

        # 计算大尺寸目标框的损失函数
        with tf.name_scope('bigger_box_loss'):
            loss_lbbox = self.loss_layer(self.conv_lbbox, self.pred_lbbox, label_lbbox, true_lbbox,
                                         anchors=self.anchors[2], stride=self.strides[2])

        with tf.name_scope('giou_loss'):
            giou_loss = loss_sbbox[0] + loss_mbbox[0] + loss_lbbox[0]

        with tf.name_scope('conf_loss'):
            conf_loss = loss_sbbox[1] + loss_mbbox[1] + loss_lbbox[1]

        with tf.name_scope('prob_loss'):
            prob_loss = loss_sbbox[2] + loss_mbbox[2] + loss_lbbox[2]

        return giou_loss, conf_loss, prob_loss

要点总结

• 边界框损失评价指标：IOU，GIOU，以及损失函数构造
• 置信度损失指标，focal_loss + sigmoid_cross_entropy_with_logits
• 分类损失：sigmoid_cross_entropy_with_logits

---

IOU的计算

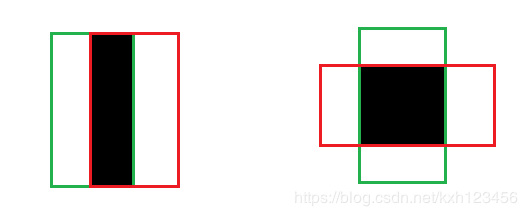
IOU（Intersection over Union），计算两个矩形重叠面积和并集面积的比值。目标检测算法中，通常计算预测的边界框和真实边界框的面积的交并比。在anchor-based的目标检测算法中，不仅可以判定正负样本，还可以计算预测框和真实框的距离。图示如下：

根据图示，可以很容易计算IOU，具体步骤如下：

1. 计算两个边界框的左上角坐标的最大值
2. 计算两个边界框的右下角的最小值
3. 根据 1. 和 2. 可以得到重叠区域，并计算重叠面积，i_area.
4. 计算两个边界框的并集面积，u_area=两个边界框面积和 - 重叠面积
5. 计算 iou = i_area/u_area.

IOU的优点：

1. IOU具有度量的特征，比如非负性、不确定性、对称性和三角不等性，因此可以作为距离度量，$L_{iou}=1-IOU.$
2. IOU具有空间尺度不变性，即两个矩形框的相似性与所在的尺度无关。

IOU的不足：

1. 如果两个边界框不重叠，则计算的IOU为0，无法衡量两个目标之间的距离。在这种无重叠目标的情况下，如果IOU作为损失函数，梯度为０，无法优化。
2. IOU无法区分两个对象之间的对齐方式。确切地讲，不同方向上有相同交叉级别的两个重叠对象的IOU会完全相等。
   

GIOU的计算

giou（generalize intersection over union）是在iou的基础上发展而来，当然也是为了解决iou存在的问题。如下图所示，红色边界框A，蓝色边界框B，A和B的最小包围框C，计算图示如下：

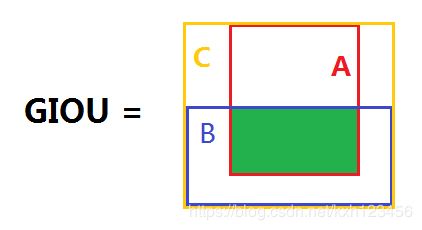
GIOU的算法流程： 1. 计算IOU; 2. 找到A和B的最小包围框C; 3. 按照下面的公式计算GIOU.

GIoU作为度量时的性能：

1. GIoU作为距离时，$L_{GIoU}=1-GIoU$满足损失函数的基本要求，非负性，不确定性，对称性以及三角不等性。
2. 对尺度不敏感。
3. GIoU始终是IoU的下限，即GIoU(A,B) <= IoU(A,B)。当A,B形状相似，并且无限接近时，$$li{m}_{A\to B}GIoU(A,B)=IoU(A,B)$$
4. GIoU值域为 -1≤ GIoU(A,B) ≤ 1. 当A，B完全重合时，GIoU(A,B) = IoU(A,B) = 1. 当(A∪B)/C→0 时，也即是A∪B的面积相对于C非常小时，此时$IoU->0$，GIoU收敛于-1。
5. GIoU考虑到了 IoU 没有考虑到的非重叠区域，能够反应出 A,B 重叠的方式。

GIOU和IOU作为损失函数的算法流程：

交叉熵损失函数

1. 熵（Entropy）
2. 交叉熵
3. sigmoid和softmax区别和联系
4. tensorflow中的损失函数应用

---

熵的概念和定义
熵是用来衡量一个系统的信息量的指标，表示所有信息量的期望，也称之为信息熵。它具有以下3个特点：

• 单调性，发生概率越高的事件，其携带的信息量越低；
• 非负性，信息熵可以看作为一种广度量，非负性是一种合理的必然；
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，这也是广度量的一种体现。

熵的定义：
$$H(x)=-\sum _{x\in X}p(x)lo{g}^{p(x)}$$
其中，$I(x)=-lo{g}^{p(x)}$称之为事件x的信息量，p(x)值越大，不确定性越小，则信息量越少。
交叉熵的概念和定义

介绍交叉熵之前，先简单回顾下散度的知识，KL(Kullback-Leibler Divergence)散度：
  KL散度又称之为相对熵，用来描述两个概率分布P和Q的差异性。两个分布的差异性越大，则散度越大。公式定义如下：$$D_{KL}(p||q)=\sum _{i=1}^{N}p(x_i)log(\frac{p(x_i)}{q(x_i)})$$
其中，KL散度是非对称的，即$D(p||q)$不一定等于$D(q||p)$，常作为优化的目标。

对上述散度公式变形如下：
$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{N}p(x_i)log(p(x_i))-\sum _{i=1}^{N}p(x_i)log(q(x_i))\\ & =H(p(x))+[-\sum _{i=1}^{N}p(x_i)log(q(x_i))]\end{array}\text{\hspace{1em}(1)}$$

其中，$p(x_i)$是真实事件的概率，等同于标签，$q(x_i)$是拟合的分布值，等同于预测值。因此公式(1)的第一项变为$-H(p(x))$就是x的熵，优化过程中是不变的，所以不予以考虑。而后一部分就是交叉熵损失函数，N表示样本数量，数学定义如下：
$$H(p,q)=-\sum _{i=1}^{N}p(x_i)log(q(x_i))$$

Sigmoid函数：

机器学习中，经常出现的logistic函数，也就是sigmoid函数。它将值映射到（0,1）之间。通常作为神经网络的激活函数使用，公式定义如下：
$$\delta (x)=\frac{1}{1+e^{-x}}$$

Softmax函数：

softmax函数，又称之为归一化指数函数。它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式表达出来，公式如下：
$$softmax(x_i)=\frac{e^{x_i}}{{\sum }_i^n{e}^{x_i}}$$

Tensorflow中的损失函数：

1. tf.nn.sigmoid_cross_entropy_with_logits()
   输入参数如下：
     _sentinel: 内部不使用，忽略该参数
     labels：真实标签
     logits：网络预测输出
     name：该操作的名字
   函数返回值：
     A Tensor of the same shape as logits with the componentwise logistic losses.
   函数的功能和适用场景，见tensorflow文档解释如下，
     " Measures the probability error in discrete classification tasks in which each class is independent and not mutually exclusive. For instance, one could perform multi label classification where a picture can contain both an elephant and a dog at the same time."
     主要用于评测离散型分类任务中的概率误差。此类分类任务中，每一类是独立不互斥的关系。比如，经常用于多标签分类任务，并且每一张图片可以同时包括多个类别，大象或者狗。
   内部计算处理：
     为了表述的简单，令x=logits，z=labels，逻辑损失计算如下，
   $$\begin{array}{rl}loss& =z\ast [-log(sigmoid(x))]+(1-z)\ast [-log(1-sigmod(x))]\\ & =z\ast (-log(\frac{1}{1+e^{-x}})+(1-z)\ast (-log\frac{e^{-x}}{1+e^{-x}}))\\ & =z\ast log(1+e^{-x})+(1-z)\ast [-log(e^{-x})+log(1+e^{-x})]\\ & =z\ast log(1+e^{-x})+(1-z)\ast (x+log(1+e^{-x}))\\ & =(1-z)\ast x+log(1+e^{-x})\\ & =x-x\ast z+log(1+e^{-x})\end{array}$$
     当x<0时，为了防止$e^{-x}$溢出，将上述公式更改如下，
   $$\begin{array}{rl}loss& =x-x\ast z+log(1+e^{-x})\\ & =log(e^x)-x\ast z+log(1+e^{-x})\\ & =-x\ast z+log(1+e^x)\end{array}$$
     因此，为了保证训练的稳定性和避免溢出，使用下面的公式：
   $$\begin{array}{r}max(x,0)-x\ast z+log(1+e^{-abs(x)})\end{array}$$

2. tf.nn.softmax_cross_entropy_with_logits()
   输入参数如下：
     _sentinel：通常忽略该参数。
     labels：标签数据，label[i]的每一行必须是有效的概率分布，总和为1，通常设置为one-hot[1 0 0 0].
     logits：网络的原始输出，
     dim：class的维度，通常为-1.
     name：操作的名字.
     axis：维度对齐.
   函数的功能和适用场景，见tensorflow文档解释如下
     " Measures the probability error in discrete classification tasks in which the classes are mutually exclusive (each entry is in exactly one class). For example, each CIFAR-10 image is labeled with one and only one label: an imagecan be a dog or a truck, but not both.."
     度量类分类任务的误差，类之间是互斥的关系。比如，cifar10中，每张图片必须是一类.

参考链接

IOU和GIOU详解
交叉熵的理解