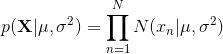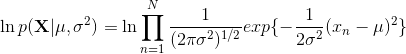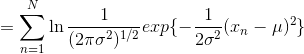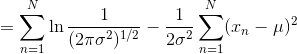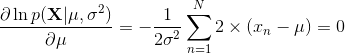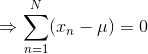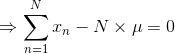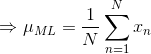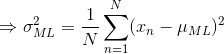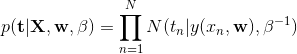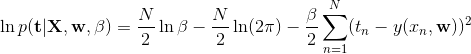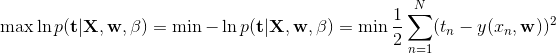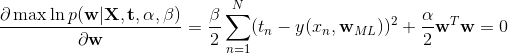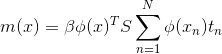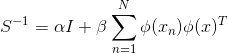一元高斯分布（Univariate Gaussian Distribution）（详细说明，便于理解）

1、一元高斯分布的定义

高斯分布也叫正态分布，主要用于连续变量的分布。假设有一变量 ，则其高斯分布形式为：

                                   

式中  是均值（mean）， 是方差(variance)，方差的平方根 叫做标准误（standard deviation），方差的倒数  叫做精度（precision）。

高斯分布满足： 

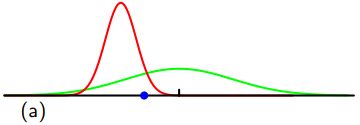
高斯分布是归一化的（如下图（左）所示）：                                                            

变量  在高斯分布下的期望：

                                           

证明上式：令 ，则

                                      

                                              

                                             

式中第一项是奇函数，且在内积分，所以为0；第二项积分部分为1，所以第二项为 ，即 。

  表示  在高斯分布下的平均值。相似的，二阶矩为（the second order moment）：

                                            

                                        

证明上式：令 ，则

 

         

           

式中第二项为奇函数，且在内积分，所以为0；第三项积分部分为1，所以第三项为 ，因此现在只需要求出第一项即可。在第一项中 ，所以第一项等于 ：

                         ,   

所以 ，即

                                       

一个分布的最大值称为它的模式(mode)。对于高斯分布，均值就是其模式。

注：对于概率函数：零阶矩表示点的总概率（也就是1）；一阶矩表示 期望；二阶（中心）矩表示 方差；三阶（中心）矩表示 偏斜度；四阶（中心）矩表示峰度。

                                      

                                                左                                                                                            右

假设有一观测数据集 ，表示标量  的N个观测值。假设观测是独立来自均值为  、方差为  且  和  未知的高斯分布，则如何从已给的数据集中确定这些参数？

2、参数  和  的求解方法

2.1 最大化似然函数

从同一分布中独立出来的数据点被称为是独立的同分布的（independent and identically distributed，i.i.d.）。两个独立事件的联合概率等于每个事件的边缘概率的乘积。因此，数据集的概率为：

                                                    

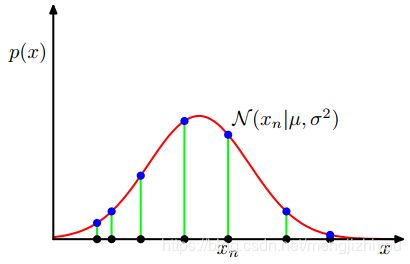
将上式看做关于   和  的函数，则上式是高斯的似然函数。如上图（右）所示，红色曲线是高斯分布的似然函数，黑点表示  的数据集，蓝色点是似然函数的值，使似然函数最大化涉及到调整高斯分布的均值和方差，从而使乘积最大化。

注：似然：指在已知数据下求参数的概率。

利用观测数据集确定概率分布中参数的一个常用标准是找到使似然函数最大化的参数值。为什么是在给定参数的情况下最大化数据的概率而不是在给定数据的情况下最大化参数的概率？这两个标准是相关的，后面会讨论。

目前是通过最大化似然函数来确定未知参数  和  的值。实际中，似然函数的对数取最大值更为方便。因为对数是自变量的单调递增函数，所以函数对数的最大值等于函数本身的最大值。

取对数的原因：简化后续的数学分析，大量小概率的乘积很容易影响计算机的数值精度，这可以通过计算对数概率的和来解决。

因此对数似然函数为：

                                       

                                                                

                                                                

                                                                

上式对  最大化，则最大似然(maximum likelihood)的解为：

                                                      

                                                                           

                                                                          

                                                                          

就是所有样本的均值，类似的对最大化，则方差的最大似然解为：

                                                         

                                                                          

                                                                         

即用样本方差来衡量样本均值 。

但是似然函数会低估分布的方差，这种现象叫做偏差，跟过拟合有关。 首先 ， 是数据集  的函数的最大似然解。这些数据集本身来自高斯分布，有参数  和  ，则：

                                                                  

                                                                   （推导过程）

因此通过平均最大化似然估计会得到正确的均值但是会低估方差因为因子 。

下面对方差参数的估计是无偏的：

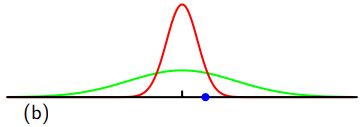
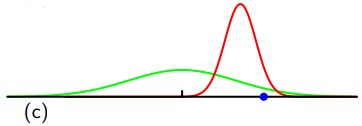
 如何使用最大似然法来确定高斯分布的方差？如下图所示，绿线代表真正的高斯分布，三条红色曲线代表三个数据集用最大似然的结果拟合的高斯分布，每个数据集包含两个点如蓝色点所示。三个数据集的平均值是正确的，但是方差被系统地低估了，因为它是相对于样本均值测量的，而不是相对于真实均值。

   

注：随着数据点数目N的增加，最大似然解的偏差变得不那么显著，在极限N→∞时，方差的最大似然解等于产生数据的分布的真实方差。

在实践中，对于除小N之外的任何值，这种偏差都不会被证明是一个严重的问题。但是对于更复杂的模型和更多的参数，与最大似然相关的偏差问题将更加严重。最大似然偏差问题的根源在于过拟合问题。

下面用多项式曲线拟合说明最大化似然的偏差问题，从概率的角度来看待它。

曲线拟合的目的用训练数据 及其相应的目标变量值  得到的曲线对新的  进行预测得到目标变量值 。

可以用概率分布来表示目标变量值的不确定性，因此假设在给定  的条件下，对应值  有一个均值为  的高斯分布，因此：

                                                          ,    

                                                      

M 是多项式的阶数， 表示 x 的 j 次方。

如下图(左)所示，在给定  和  条件下的高斯条件分布，其均值为 ，精度是 。

用训练数据  由最大似然来确定未知参数  和  的值。假设数据是独立地来自分布，则似然函数为：

                                            (式0）

对似然函数取对数：

                               (式1）

首先考虑多项式系数的最大似然解 。在求  时，前面两项没有 ，所以可以去掉。同时对数似然乘以一个正的系数不会改变  最大值的位置，因此可用  代替 。最后通过最小化负的似然函数来替代最大化似然函数，得到最小化误差函数，即：

                 

相当于最小化平方和误差函数。

式1对  最大化得：

算出参数  和  的值后，可以用新的  值来预测。通过概率模型（也叫预测分布）来表示  的概率分布，而不是简单的点估计。预测分布概率模型为：

                                                                            

 

                              

                                                 左                                                                                            右

2.2 最大化后验概率

现在考虑贝叶斯的方法，引入多项式系数 的先验分布。为了简单起见，只考虑  形式的高斯分布：

                             (式2）

 是分布的精度（），M +1 是一个 M 阶多项式向量 中元素的总数。变量如  ，控制着模型参数的分布，叫做超参（hyperparameters）。 

根据贝叶斯定理， 的后验分布和先验分布与似然函数的乘积成正比，即：

                                             (式3）

通过找到给定数据  的最可能值确定 ，即通过最大化后验分布（maximum posterior, MAP）。

                             

                                                             

                                                             

                                                              

上式对  最小化，则：                          

                               

从上式可以看出最大化后验分布等价于最小化正则化误差平方和。正则化参数 。

尽管有前验分布，但仍在对  做点估计，所以这还不是贝叶斯方法。

在完全的贝叶斯方法中，应该应用概率的和和积规则，这就要求对  的所有值进行积分。这种边缘化是贝叶斯模式识别方法的核心。

对新变量  的预测分布形式为：

                                                 

                                                 

 是参数的后验概率，可以通过式3的右边进行归一化得到。                                                   

上述预测分布可由高斯形式给出：

                                                  

                                      mean:  

                                 variance:     (式4）

                                 S matrix:  

 是单位矩阵（unit matrix），。  

预测分布的均值和方差依赖 。对于式4，第一项是方差表示  的预测值的不确定性因为目标变量有噪声，第二项来自于参数w的不确定性，是贝叶斯处理的结果。

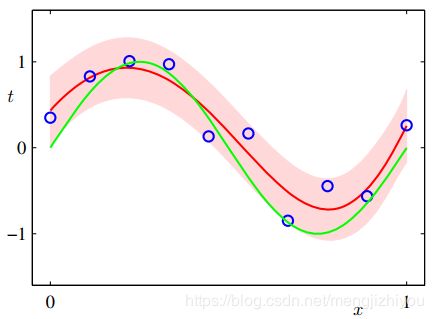
回归问题的预测分布如上图（右）所示：该图是多项式曲线在贝叶斯处理下的预测分布结果。M=9，，。红色表示预测分布的均值，红色区域表示均值的  的标准误。

 

参考：

1、PRML

2、https://blog.csdn.net/libing_zeng/article/details/74905378