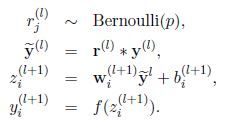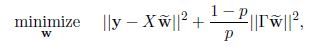【论文精读】Dropout: A Simple Way to Prevent Neural Networks from Overfitting
Dropout: A Simple Way to Prevent Neural Networks from Overfitting
原文链接:Dropout: A Simple Way to Prevent Neural Networks from Overfitting
来填坑了,上次读了《Deep Learning under Privileged Information Using Heteroscedastic Dropout》这篇论文(笔记看这里),感觉有很多东西还没弄懂,原论文也多次提到了这篇文章,今天来拜读一下(貌似Gaussian Dropout就是在这里被首先提出来的)。这篇文章很长,实验部分就不多讲了,重点看看作者对于Dropout的理解和认识。
Abstract
深层神经网络是非常强大的机器学习系统。然而,在这样的网络中,过拟合是一个严重的问题。大型网络的使用速度也较慢,这使得在测试时结合许多不同的大型神经网络的预测来处理过拟合问题变得非常棘手。Dropout是解决这个问题的一种技巧。关键的想法是在训练过程中,从神经网络中随机丢弃神经元(以及它们的连接)。这就防止了神经元之间过度的协同适应。在训练过程中,dropout技巧会从指数级的的不同的“稀疏”网络中抽取样本。在测试时,就可以很容易地估计出所有这些稀疏网络的预测结果的平均。这显著地减少了过拟合,并且比其他正则化方法有了很大的改进。我们证明,drop改进了神经网络在视觉、语音识别、文档分类和计算生物学等监督学习任务上的性能,获得了许多基准数据集state-of-the-art结果。
关键词:neural networks, regularization, model combination, deep learning
Introduction
深度神经网络深层的结构让他们有很强的学习能力。然而,在训练数据有限的情况下,这些复杂的关系有许多是采样噪声的结果,因此它们将存在于训练集中,而不存在于真实的测试数据中,即使它们来自相同的分布(就是说在训练集数据少的情况下,深层的网络会把噪声造成的输入输出之间复杂的关系也完美拟合,使其不再具有好的泛化能力)。解决方法主要有:提前终止、L1和L2正则化、软权重共享(soft weight sharing)。
不考虑计算的成本,对于固定尺寸的模型来说,最好的正则化策略就根据训练数据的后验概率大小加权平均所有的可能的参数。但对于较复杂的网络,这种方法计算量太大了。所以作者采用另一种对指数数量级的共享参数的网络的进行平均策略。
组合不同的大型网络是最好的方法,但是却不可行,一方面没有那么多数据去训练,训练那么多网络很耗时,找到合适的超参也很难,同时在测试时响应速度会很慢。
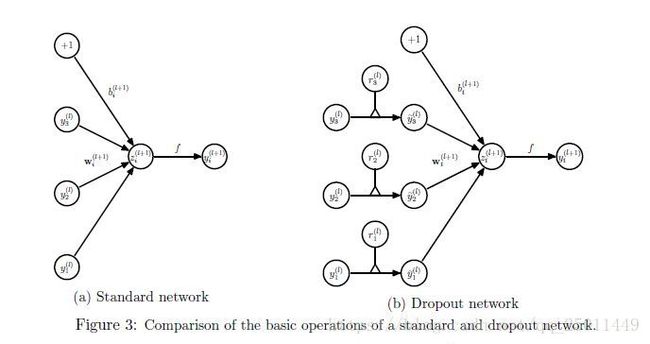
图1介绍了Dropout的用法,通常dropout率 p p p可以通过验证集确定,或者设为0.5(这样产生的可能情况是最多的),但是输入层的dropout率要接近1。
使用了Dropout技巧,如果一个网络有 n n n个神经元,那么就有 2 n 2^n 2n种子网络结构可能出现,但是由于权值都是共享的,所以参数还是 O ( n 2 ) O(n^2) O(n2)数量级的。
测试时,直接用子网络输出结果的平均不是可行的 ,但使用子网络权值的加权平均构成新的网络却可以表现很好。为了让这个组合的网络输出的期望和真实的期望相同,那么在子网络组合时,应该将权值都乘以dropout率 p p p。这种方法也能用在受限波尔茨曼机(RBM)中。
Motivation
Dropout的动机来自于关于性别在进化中的作用的理论。有性生殖包括从一个亲本和另一个亲本中提取一半的基因,加入非常少量的随机突变,并将它们结合产生受精卵。无性繁殖是通过父母基因的拷贝中加入微小突变来创造后代。无性繁殖应该是一种更好的方法来优化个体的健康,这似乎是合理的,因为一组良好的基因组合在一起可以直接传递给后代。另一方面,有性生殖很可能会破坏这些共同适应的基因,特别是如果这些基因的数量很大,而且直觉上,这应该会降低已经进化出复杂的共同适应的生物体的适应性。然而,有性繁殖是最先进的生物进化的方式。
对有性生殖优势的一种可能解释是,从长期来看,自然选择的标准可能不是个体特性,而是基因的混合能力。就是说那些能够和更多随机的基因协作的基因才是更加健壮的。因此一些基因必须要自己学会做一些事而不只是跟很多其他基因合作,这种合作会减少个体适应性。类似地,随机的选择dropout可以增加隐层神经元的健壮性。
有个密切相关但却略有不同的例子,十个阴谋,每个五人参与和一个大阴谋五十人参与相比,显然前者获得一次成功概率较大。一个复杂的共同协作的网络在训练集表现会很出色,但到测试集中,出现了很多新的数据,他就不如很多个更为简单的协作神经元工作的效果好。
Related Work
Dropout可以被解释为一种通过在隐藏的单元中添加噪声来调节神经网络的方法。Vincent et al.(2008, 2010)曾在去噪自动编码器(DAEs)的背景下,将噪声添加到自动编码器的输入单元中,并训练网络重构无噪声输入。作者的工作扩展了这一思想,展示了dropout可以有效地应用到隐藏层中,并且它可以被解释为一种模型平均的形式。作者还表明,增加噪声不仅对无监督特征学习有用,而且可以扩展到有监督学习问题。事实上,我们的方法可以应用于其他基于神经的架构,例如,Boltzmann机器。虽然5%的噪声通常对DAEs最有效,但我们发现我们在测试时应用的加权缩放程序使我们能够使用更高的噪声级别。放弃20%的输入单元和50%的隐藏单元通常是最优的。
由于dropout可以看作是一种随机正则化技术,因此很自然地要考虑它的确定性对应物,而确定性对应物是通过边缘化噪声得到的(就是把和dropout效果相同的正则项提取出来)。在本文中,我们证明了,在简单的情况下,可以用边缘化的方法提取出来,从而获得确定性的正则化方法。最近,van der Maaten et al.(2013)也探究了与不同指数族噪音分布相对应的确定性调节因子,包括辍学者(他们称之为\blankout noise)。然而,他们将噪声应用到输入中,只探索没有隐藏层的模型。Wang和Manning(2013)提出了一种通过边缘化dropout噪声来加速dropout的方法。Chen等人(2012)在去噪自动编码器的背景下探讨了边缘化问题。
在dropout中,我们随机地最小化噪声分布下的损失函数。这可以看作是最小化期望损失函数。Globerson and Roweis (2006);Dekel et al.(2010)研究了另一种情况,即当对手选择放弃哪个unit时,损失最小化。在这里,可以删除的单元的最大数量不是噪声分布,而是被取消的。然而,这项工作也没有探究隐藏单元的模型。
Model Description
Dropout技巧很简单,可由以下公式描述:
其中 r ( l ) \textbf r^{(l)} r(l)表示一个由多个独立的服从相同伯努利分布的变量构成的向量, ∗ * ∗表示点乘,即对应元素相乘,第 l l l层的输出 y ( l ) \textbf y^{(l)} y(l)经过dropout变为 y ~ ( l ) \widetilde {\textbf y}^{(l)} y (l)。 l + 1 l+1 l+1层的输入和输出算法不变。在应用BP进行训练时,只对子网络的参数求导即可,测试时子网络的参数需要被缩放: W t e s t ( l ) = p W ( l ) W^{(l)}_{test}=pW^{(l)} Wtest(l)=pW(l)。如图二所示。
Learning Dropout Nets
这一节介绍dropout的网络是如何训练的。
Backpropagation
带dropout的神经网络和普通神经网络训练起来差不多,唯一的区别就是在一个mini-batch中参数的更新只发生在子网络中,那些被dropout屏蔽的网络神经元参数都不会被更新。那些用来改善SGD效果的算法,比如:momentum、退火法、L2正则化在有dropout的情况下也都适用。
另一种对于dropout很有用的策略是将每层隐层权重的模的大小限制为 c c c(感觉类似于L2正则化)。这样可以限制参数在learning rate很大的情况下不至于blowing up。
Unsupervised Pretraining
Dropout如果用在预训练的网络上,需要先把权值乘以 1 / p 1/p 1/p,learning rate尽量选小一点,不然会抹去预训练时学到的信息。
Experimental Results
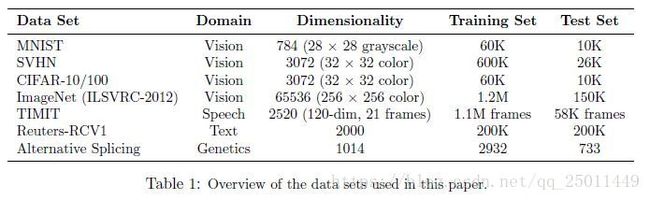
作者在不同类型的很多数据集上做了实验,具体数据集情况见下表1,得到的实验结果均证明dropout的有效性。
具体的实验结果有兴趣的话可以到原论文里查看。
Salient Features
这一节为了探究dropout为啥有效,探究了以下几个方面:dropout对特征产生的影响;对隐层神经元激活值稀疏性的影响;dropout率、神经网络规模和训练集规模大小对dropout效果的影响。
Effect on Features
图7是拥有256个修正线性单元的一层隐层的自编码器在MNIST上的训练结果,很明显地看出,左边没有dropout的情况下,每个单元并没有很明确地要去检测某个图像特征,这是由于单元之间的相互适应性太强,需要组合在一起才能比较好地工作,但是就右图有dropout的情况而言很明显可以看出,每个单元都在检测一种边缘、笔画或者点,也就是说每个单元之间没有那么强的相互适应性。泛化能力会强很多。
Effect on Sparsity
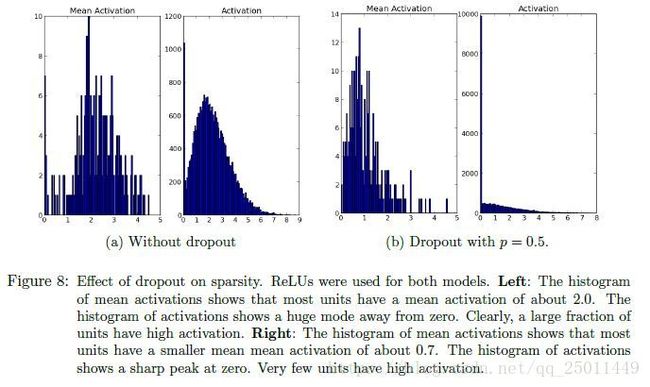
图8展示了dropout对隐层激活值稀疏性的影响,可以看出加入了dropout以后激活值的分布向0靠近,稀疏性明显增加。
Effect of Dropout Rate
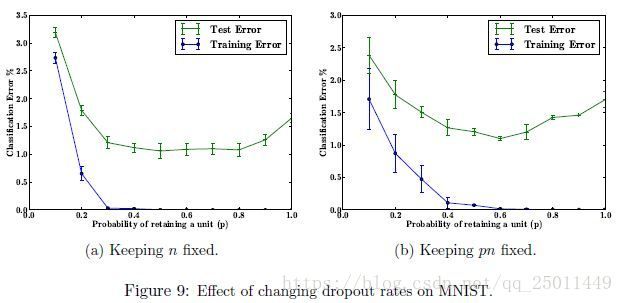
这一小节探究dropout率(神经元保留率)对效果的影响。作者从下面两种情况进行比较:
- 隐层神经元个数固定( n n n fixed)。
- 在经过了dropout后被保留的神经元期望是恒定的( p n pn pn fixed).
结果如图9所示,值得注意的是,如果保持 p n pn pn不变,那么在 p p p很小时,误差要比保持 p p p不变时小很多。两种情况下,都是在0.5左右得到最小的测试误差。(我感觉这个实验这样纵向对比不是很合理)
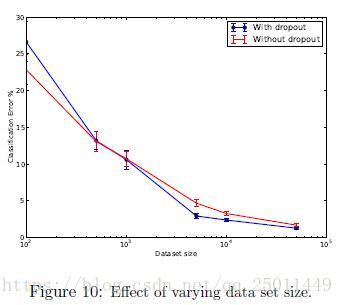
Effect of Data Set Size
这个结果很有意思,在训练数据极小的情况下,即使加了dropout也不会使训练效果变好,因为数据集太小时,就算加了dropout网络还是有足够多的参数使结果过拟合,这个很好理解。
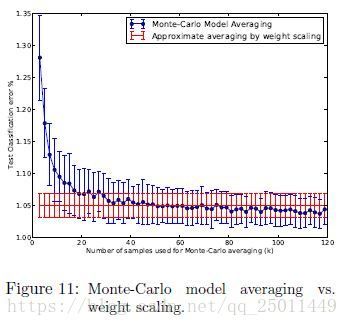
Monte-Carlo Model Averaging vs. Weight Scaling
在测试时需要把子网络组合起来,使用文中提到的Monte-Carlo Model Averaging模型,当采样的 k k k很大时,效果很好,但是很耗时,直接使用前面提到的Weight Scaling,即把子网络权值按照dropout率缩放后组合的方式更有效率。
Dropout Restricted Boltzmann Machines
这里把dropout技巧用在了受限波尔茨曼机,挖个坑等学了RBM再来感受一下。
Marginalizing Dropout
这一小节作者将dropout随机的部分边缘化,使dropout的效果边缘化到损失函数,使其成为一种“确定性”的模型。
Linear Regression
把dropout应用到最简单的线性回归,即仅在输入 X ∈ R N × D X \in \mathbb{R}^{N \times D} X∈RN×D的基础上点乘 R ∈ { 0 , 1 } N × D R \in \{0, 1\}^{N \times D} R∈{0,1}N×D的Bernoulli矩阵,那么优化问题就会由:
min w ∥ y − X w ∥ 2 \min \limits_{\textbf w}~~~~~~~~ \left \| \textbf y-X\textbf w \right \|^2 wmin ∥y−Xw∥2
变为:
化简后:
其中:
![]()
或者还可以写成:
其中:
![]()
这个式子的格式有没有很是熟悉。
Logistic Regression and Deep Networks
这里作者也没给出具体的说明。
Multiplicative Gaussian Noise
这里作者讨论了将Bernoulli随机数改为Gaussian随机数的效果,在Bernoulli情况下如果单元保留的概率为 p p p,那么方差为 ( 1 − p ) / p (1-p)/p (1−p)/p,在Gaussian的情况下将方差也设为 ( 1 − p ) / p (1-p)/p (1−p)/p,得到的实验结果如下表10,对于这样的结果,作者解释为,Gaussian的情况下熵要高一些。
Conclusion
总结的展望中作者主要谈了dropout加速问题,由于随机舍弃掉一些单元会使得参数的更新很“noisy”,解决办法可以是找到一个有相同效果的正则项来代替dropout。