不相交集（并查集）

不相交集是解决等价问题的一种有效的数据结构。

一、等价关系

等价关系定义如下：
1） 自反性：对于所有的a属于集合S， a与a有关系；
2） 对称性：如果a与b 有关系， 则b与a 有关系；
3） 传递性：如果a有b 有关系， b与c有关系， 则a 与 c 有关系；
在不想交集类中， 所有具有等价关系的类都在一个集合中，称为等价类； 不同的集合之间不存在等价关系；
为确定a 和 b是否具有关系， 我们只需要确定a 和 b 是否属于同一个等价类中；

一开始， 输入数据是N个数据， 每一个数据就是一个等价类（每个等价类中只有iyge元素）；因此，初始时候，每个元素都是不相交的；
对不相交集允许两种操作：
1） find 操作
find 函数返回包含给定元素 的等价类的名字；
2） union 操作
如果要在a 和 b 之间建立等价关系， 首先需要确定a 和 b 是否已经具有等价关系了， 这可以通过对a 和 b执行find操作并检验他们是否在同一个等价类中完成。如果a 和 b 之间没有等价关系， 就将a 和 b 的两个等价类合并成一个新的等价类。

注意， 我们不进行任何比较元素相关的值得操作，只需要知道他们的位置。因此， 可以假设所有的元素均已从0到N-1 顺序编号， 并且编号方法容易由某个散列方案确定；
find操作返回的等价类的名字是很随意的， 不同的情况下a元素的等价类的名字可能会不同， 确定a 和 b是否有等价关系， 只要的是find(a) == find(b)

不相交集的find的操作在最坏的情况下运行时间为常数（当集合中每一个元素都是一个等价类的时候）；
union 操作的最坏运行时间是常数（两个最大等价类合并到时候）；
上述两个操作不能同时以常数最坏运行时间运行；

在执行union的时候， 通常将较小的等价类的名字改成较大的等价类的名字， 对于N-1 次合并到总的时间开销为O(NlogN)。 其原因在于， 每个元素可能将它的等价类最多改变logN 次；因此， 每次等价类改变时他的新的等价类至少是其原来等价类的两倍大小。使用这种方法， 任意顺序的M次find 和 N-1次union 最多花费 O(M + NlogN)的时间；

二、数据结构

使用树结构表示一个等价类， 树的集合是森林， 森林表示等价类的集合；
等价类的名字就是树的根；
使用一个数组， 数组的每个成员s[i] 表示元素i的父亲， 如果元素i是根， 那么s[i] = -1;

union 操作：
将一棵树的根雕父链 链接到另一棵树的根结点， 从而合并这两棵树。
find 操作：
对元素x的一次find(x) 操作通过返回这棵树的根完成；执行find的操作花费的时间与x结点深度成正比；x结点的深度可能是N-1,因此find操作的最坏情形的代价是O(N)；
M次连续操作的最坏情形是O(MN)；

相关代码如下：

class DisjSets {
public:
	explicit DisjSets(int numElements);
	int find(int x) const;
	int find(int x);
	void unionSets(int root1, int root2);

private:
	vector<int> s;
};

DisjSets::DisjSets(int numElements) :s(numElements) {
	for (auto i = 0; i < s.size(); i++)
		s[i] = -1;
}

void DisjSets::unionSets(int root1, int root2) {
	s[root2] = root1;
}

int DisjSets::find(int x)const {
	//递归调用的边界条件
	if (s[x] < 0)//x元素的父节点为-1，则x就是根节点，返回x
		return x;
	else
		return find[s[x]];//查找x的父节点
}

三、优化union操作

上述union的操作是比较随意的， 只是让第二棵树成为第一棵树的子树；
改进的方法， 使得较小的树称为较大的树的子树——按大小求并， 这样的改进可以控制树的深度不至于过大；任何结点的深度均不会超过logN；当一棵树的深度随着一次union的结果而增加的时候， 该结点被放置在至少是他以前所在树两倍大点一棵树上。因此， 深度最多可以增加logN次；
find 操作的运行时间是O(logN), 连续M次操作则花费O(MlogN)。

上述改进需要记住每一个树（等价类）的大小；由于父节点的数组值s[i] 是-1， 可以使用-k中的k表示树的大小；
业界已经证明， 如果按照大小求并原则连续M次操作， 平均需要O(M)时间。 这是因为当随机的union执行时候， 整个算法一般只有一些很小的集合与大集合合并；
改进的union 代码如下所示：

另外一种改进是按照高度求并，代码如下：

void DisjSets::unionSets(int root1, int root2) {
	// root1是等价类1的根， root2是等价集2的根
	if (s[root2] < s[root1])//负数比较， root2的高度更大
		s[root1] = root2;
	else {
		if (s[root1] == s[root2])
			s[root1]--;//root1的深度+1
		s[root2] = s[root1];
	}
}

四、路径压缩

并查算法对于连续M个指令的时间复杂度， 平均是线性的。但是O(MlogN)的最欢情形还是相当容易发生的；
例如， 将所有的集合放在一个队列中， 并重复让前两个集合出队，再将这两个集合的并入对，就会出现最坏情形；
分析find 和union的代码可知：
find中存在递归调用， 其代码复杂度与树的深度有关；
union代码中只是简单的判断代码，代码复杂度O(1)；
对于一个操作序列， 如果find操作比较多的话， 其运行时间会比较大；

对于union算法， 没有改进的空间了；
对于find算法， 还可以改进；
1） 使用路径压缩改进find算法
路径压缩在一次find操作期间执行与用来执行union的方法无关。
设操作find(x) ,路径压缩的效果是， 从x到根的路径上的每一个结点都使他的父结点变为根；
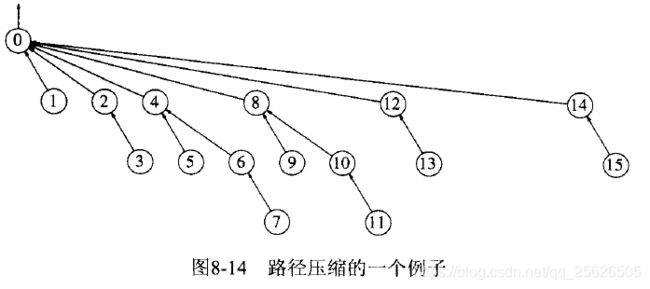
例如， 下图经过find(14) 的效果；

路径压缩的实现代码如下：

int DisjSets::find(int x){
	if(s[x] < 0)
		return x;
	else
		return s[x] = find(s[x]);
}

当存在多个union操作的时候， 路径压缩是一个好办法。因为存在许多深层次的节点， 可以通过路径压缩是这些深层次的节点靠近根；

路径压缩与按大小求并完全兼容， 因此这两个例程可以同时实现；
路径压缩不完全与按高度求并兼容， 因为路径压缩会改变树的高度。

五、并查集的应用