论文阅读笔记|论文总结 AdaGAN、GAIL、SeqGAN等四篇

论文总结

AdaGAN: Boosting Generative Models

AdaGAN论文阅读笔记

A Connection Between GAN, IRL and EBM

###Motivation

Then maximizing likelihood will lead to a distribution which “covers” all of the modes, but puts most of its mass in parts of the space that have negligible density under the data distribution.

A generator trained adversarially will instead try to “fill in” as many of modes as it can.

Complex multimodal distribution很难通过maximize likelihood评估密度分布。它会将尽可能地覆盖$P_{data}$而使其$P_G$主要分布在各个mode之间的空白区域；而GAN则会尽量填满$P_{data}$而使$P_G$更接近$P_{data}$。

###Summary

IRL methods are in fact mathematically equivalent to GANs.

In particular, a sample-based algorithm for maximum entropy IRL and a GAN.

Definition

Boltzmann distribution

$p_{\theta }(\tau )=\frac{1}{Z}{e}^{-E_{\theta }(\tau )}$.

Partition function

$Z=\int e^{-E_{\theta }(x)}dx$.

Discriminator loss

${\mathcal{L}}_{discriminator}(D)={\mathbb{E}}_{x\sim p}[-\log D(x)]+{\mathbb{E}}_{x\sim G}[-\log (1-D(x))]$.

Generator loss

${\mathcal{L}}_{generator}(G)={\mathbb{E}}_{x\sim G}[-\log D(x)]+{\mathbb{E}}_{x\sim G}[\log (1-D(x))]$.

Calculation

使用cost function $c_{\theta }$表示energy $E_{\theta }$。

$Z=\int e^{-c_{\theta }(\tau )}d\tau$

使用sampling distribution $q(\tau )$估算$Z$。

${\mathcal{L}}_{cost}(\theta )={\mathbb{E}}_{\tau \sim p}[c_{\theta }(\tau )]+\log ({\mathbb{E}}_{\tau \sim q}[\frac{e^{-c_{\theta }(\tau )}}{q(\tau )}])$

通常最小化$q(\tau )$与$\frac{1}{Z}{e}^{-c_{\theta (\tau )}}$的KL散度来更新$q(\tau )$，其等价于最小化learned cost同时最大化熵值（最小化交叉熵等价于最小化KL散度，花书P49）。

${\mathcal{L}}_{sampler}(q)={\mathbb{E}}_{\tau \sim q}[c_{\theta }(\tau )]+{\mathbb{E}}_{\tau \sim q}[\log q(\tau )]$

为了防止$q(\tau )$方差过大。我们设mixture distribution $\mu =\frac{1}{2}p+\frac{1}{2}q$其中$p(\tau )$为demonstration distribution的粗略估算。

${\mathcal{L}}_{cost}(\theta )={\mathbb{E}}_{\tau \sim p}[c_{\theta }(\tau )]+\log ({\mathbb{E}}_{\tau \sim \mu }[\frac{\exp (-c_{\theta }(\tau ))}{\frac{1}{2}p+\frac{1}{2}q}])$

Conclusion

$Z={\mathbb{E}}_{\tau \sim \mu }[\frac{exp(-c_{\theta }(\tau ))}{\mu }]$.

${\partial }_{\theta }{\mathcal{L}}_{cost}(\theta )={\partial }_{\theta }{\mathcal{L}}_{discriminator}(D_{\theta })$.

${\mathcal{L}}_{generator}(q)={\mathcal{L}}_{cost}(\theta )+{\mathbb{E}}_{\tau \sim q}[\log q(\tau )]=\log Z+{\mathcal{L}}_{sampler}(q)$.

1. 最小化Discriminator loss的 $Z$ 的值可以由重要性采样（花书p285）partition function得到；
2. 对于此$Z$值，Discriminator loss与IRL cost的偏微分相等，即二者梯度下降等价；
3. Generator loss等于IRL cost减去$q(\tau )$的熵值。

###Deficiency

1. 只做了理论推导，没有做出相关实验。
2. 假设对demonstration distribution的组略估算已经具有较好的效果（IRL 算法的常用假设）。

Generative Adversarial Imitation Learning

Motivation

One approach is to recover the expert’s cost function with inverse reinforcement learning, then extract a policy from that cost function with reinforcement learning. The approach is indirect and can be slow.

instantiation

通过逆强化学习得到专家路线的cost function在通过强化学习得到策略是一种间接的过程（一次逆强化学习中需要多步强化学习的循环）。本文通过GAN，从数据中直接提取策略，就好像是通过逆强化学习后的强化学习，是一种即时性的学习方法。

Summary

Definition

Expectation with respect to the trajectory

$\Bbb{E}_\pi[c(s,a)] \triangleq \Bbb{E}[\sum _{t=0}^{{\infty}\gamma}t c(s_t,a_t)] $,where $ s_0 \sim p_0, a_t \sim \pi(\cdot |s_t)$, and $s_{t+1}\sim P(\cdot |s_t,a_t)$ for $t\ge 0$.

Maximum causal entropy IRL

${\max }_{c\in \mathcal{C}}({\min }_{\pi \in \Pi }-H(\pi )+{\mathbb{E}}_{\pi }[c(s,a)])-{\mathbb{E}}_{{\pi }_E}[c(s,a)]$ where $H(\pi )\triangleq {\mathbb{E}}_{\pi }[-\log \pi (a|s)]$.

(Maximum causal entropy IRL looks for a cost function c that assigns low cost to the expert policy and high cost to other policies.)

Minimize the expected cumulative cost

$RL(c)={\arg \min }_{\pi \in \Pi }-H(\pi )+{\mathbb{E}}_{\pi }[c(s,a)]$.

IRL primitive procedure

$IRL_{\psi}(\pi _ {E}) = \arg \max _ {c \in \Bbb{R}^{\mathcal{S} \times \mathcal{A} }} -\psi© + (\min_{\pi \in \Pi} -H(\pi) + \Bbb{E}{\pi}[c(s,a)]) - \Bbb{E}{\pi _ E}[c(s,a)] $.

(Where cost regularized by $\psi$, a (closed, proper) convex function.)

Occupancy measure

${\rho }_{\pi }:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$ as ${\rho }_{\pi }(s,a)=\pi (a|s){\sum }_{t=0}^{\infty }{\gamma }^{t}P(s_t=s|\pi )$.

(Interpreted as the distribution of state-action pairs with policy $\pi$)

Calculation

将Occupancy measure代入Expectation式中

${\mathbb{E}}_{\pi }[c(s,a)]={\sum }_{s,a}{\rho }_{\pi }(s,a)c(s,a)$

（显然这里的${\rho }_{\pi }(s,a)$已经就是一种概率分布，依据概率分布算期望）

可以证明，policy ${\pi }_{\rho }(a|s)$是occupancy measure$\rho (s,a)$唯一对应的policy，即。

${\pi }_{\rho }(a|s)\triangleq \rho (s,a)/{\sum }_{a^{\prime }}\rho (s,a^{\prime })$

描述$RL(c)$，即RL根据IRL学习到的policy

$RL\circ IR{L}_{\psi }({\pi }_E)=\arg {\min }_{\pi \in \Pi }-H(\pi )+{\psi }^{\ast }({\rho }_{\pi }-{\rho }_{{\pi }_E})$

(convex conjugate $f^{\ast }$，凸共轭)

IRL的目标是寻找一个鞍点，而RL则去揭示其他鞍点。

我们考虑policy和occupancy measure两种熵

$H(\pi )\triangleq {\mathbb{E}}_{\pi }[-\log \pi (a|s)]=-{\sum }_{s,a}\pi (a|s)\log \pi (a|s)$

$\bar{H}(\rho )\triangleq {\mathbb{E}}_{\rho }[-\log {\pi }_{\rho }(a|s)]=-{\sum }_{s,a}\rho (s,a)\log (\rho (s,a)/{\sum }_{a^{\prime }}\rho (s,a^{\prime }))$

可以证明

$H(\pi )=\bar{H}({\rho }_{\pi })$

$\bar{H}(\rho )=H({\pi }_{\rho })$

设

$L(\pi ,c)=-H(\pi )+{\mathbb{E}}_{\pi }[c(s,a)]$

$\bar{L}(\rho ,c)=-\bar{H}(\rho )+{\sum }_{s,a}c(s,a)(\rho (s,a)-{\rho }_{{\pi }_E}(s,a))$

可以证明

$L(\pi ,c)=\bar{L}({\rho }_{\pi },c)$

$\bar{L}(\rho ,c)=L({\pi }_{\rho },c)$

上述过程，讲述了如此一个推论，policy和occupancy measure是双射的。

通过构建一个cost regularize

$${\psi }_{GA}(c)\triangleq \{\begin{array}{ll}{\mathbb{E}}_{{\pi }_E}[g(c(s,a))],& \text{if c<0}\\ +\infty ,& \text{otherwise}\end{array}$$

$$g(x)=\{\begin{array}{ll}-x-\log (1-e^x),& \text{if x<0}\\ +\infty ,& \text{otherwise}\end{array}$$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FdH6dU2W-1593782415193)(C:\Users\hasee007\AppData\Local\Temp\1525432340607.png)]

构建这个cost regularizer的动机是

$${\psi }_{GA}^{\ast }({\rho }_{\pi }-{\rho }_{{\pi }_E})=\underset{D\in (0,1{)}^{\mathcal{S}\times \mathcal{A}}}{\max }{\mathbb{E}}_{\pi }[\log (D(s,a))]+{\mathbb{E}}_{{\pi }_E}[\log (1-D(s,a))]$$

后者是Jensen-Shannon divergence表达的original GAN。至此，将Imitation Learning与GAN通过凸共轭变换从理论上联系起来。

Conclusion

寻找表达式（Loss function）

${\mathbb{E}}_{\pi }[\log (D(s,a))]+{\mathbb{E}}_{{\pi }_E}[\log (1-D(s,a))]-\lambda H(\pi )$

鞍点$(\pi ,D)$：

1. 使用Adam gradient在$D_{\omega }$的参数$\omega$使表达式上升；
2. 使用TRPO在${\pi }_{\theta }$的参数$\theta$使表达式下降。

关于这个表达式：

1. 前半部分为Jensen-Shannon divergence（李宏毅PPT GAN P32），同时也是original GAN，通过构建cost regularizer ${\psi }_{GA}^{\ast }$做凸共轭变换，并将$c(s,a)=\log (D(s,a))$得到；
2. 后半部分为policy的熵值。

Deficiency

1. 在训练中，对于环境交互的样本效率不高（？），由于TRPO本身需要一些样本数量才能有用（？）。

It is not particularly sample efficient in terms of environment interaction during training.

2. model free需要更多的环境交互。

SeqGAN

Motivation

GAN has limitations when the goal is for generating sequences of discrete tokens.

The discrete outputs from the generative model make it difficult to pass the gradient update from the discriminative model to the generative model.

The discriminative model can only assess a complete sequence.

It is nontrivial to balance its current score and the future.

1. 生成模型的离散序列输出很难将辨别模型的梯度更新传递回离散模型（可由RL算法解决）。
2. 辨别模型需要对完整的序列进行辨别，如果部分生成序列时，需要平衡当前得分与未来得分（此文用Monte Carlo搜索解决，我们可以用ADA-IRL算法来解决）。

Summary

1. GAN is designed for generating real-valued, continuous data but has difficulties in directly generating sequences of discrete tokens. The “slight change” makes little sense.
2. GAN can only give the score loss for an entire sequence when it has been generated.

GAN应用于序列生成时有两大缺点：

1. GAN的设计目的是生成连续的实数，它利用辨别模型给出的判断对生成模型做微小的工作，然而对于离散模型而言，这种微小的工作不足以使之从有限的字典空间里找到对应的生成；
2. GAN的辨别模型只能对完整的生成结果进行辨别。

1. The generative model is treated as an agent of RL; the state is the generated tokens so far and the action is the next token to be generated;
2. Employ a discriminator to evaluate the sequence and feedback the evaluation to guide the learning of the generative model;
3. Regard the generative model as a stochastic parametrized policy.
4. Employ Monte Carlo search to approximate the state-action value.

相应的解决方案：

1. 将生成模型当作一个RL agent，将当前生成当作state，下一步生成当作action（RL基本思路）；
2. 建立一个Discriminator，来评估序列，并反馈给生成模型（Discriminator作为reward function）；
3. 将生成模型是做一个随机参数化的策略（应该是为了公式推导方便，这里即可使用概率分布来表达policy正如GAIL中一样）；
4. SeqGAN中使用蒙特卡罗搜索（可能耗费较多计算资源）解决缺点2；我们使用IRL的时候对于每一个state-action对都会有一个reward，再将这些reward做$\gamma$ discounted累加（Q Learning、Sarsa Lambda Learning的思想）即可。

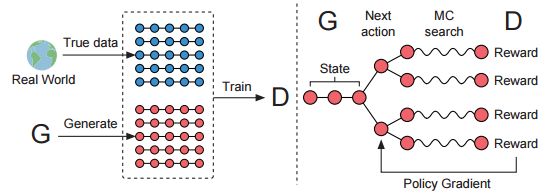
1. D is trained over the real data and the generated data by G.
2. G is trained by policy gradient where the final reward signal is provided by D and is passed back to the intermediate action value via Monte Carlo search.

Definition

Generator

$$G_{\theta }(y_t|Y_{1:t-1})$$ 可以表达为Sequence：$$Y_{1:T}=(y_1,...,y_t,...,y_T),y_t\in \mathcal{Y}$$，即In timestep $t$, state $(y_1,...,y_{t-1})$, action $y_t$.

Expected end reward

$$J(\theta )=\mathbb{E}[R_T|s_0,\theta ]=\sum _{y_1\in \mathcal{Y}}{G}_{\theta }(y_1|s_0)\cdot Q_{D_{\varphi }}^{G_{\theta }}(s_0,y_1)$$

N-time Monte Carlo search

$$\{Y_{1:T}^1,...,Y_{1:T}^N\}=M{C}^{G_{\beta }}(Y_{1:T};N)$$

Action-value function

$Q_{D_\phi}^{G_\theta}(s=Y_{1:T-1},a=y_T) = \begin{cases} \frac{1}{N} \sum_{n=1}^N D_\phi (Y_{1:T}^n), Y_{1:T}^n \in MC^{G_\beta}(Y_{1:t};N) , & \text{for $t<T$} \ D_\phi(Y_{1:t}), & \text{for $t=T$} \end{cases}$

Training

Update Discriminator

$$\underset{\varphi }{\min }-{\mathbb{E}}_{Y\sim p_{data}}[\log D_{\varphi }(Y)]-{\mathbb{E}}_{Y\sim G_{\theta }}[\log (1-D_{\varphi }(Y))]$$

Update Generator

$$\theta \leftarrow \theta +{\alpha }_h{\nabla }_{\theta }J(\theta )$$

Deficiency

1. 使用Monte Carlo搜索求未来状态奖励的平均值；
2. 使用一个CNN作为Discriminator，先将生成序列作为列向量concatenation成为一个矩阵，再做卷积和max-over-time pooling。

Diss

Behavioral cloning only tends to succeed with large amounts of data, due to compounding error caused by covariate shift.

Behavioral cloning 毕竟是一种supervised learning。

Many IRL algorithms are extremely expensive to run, requiring reinforcement learning in an inner loop.

IRL算法最大的问题在于其间接获得policy，即使用一个RL算法作为内循环。（讲道理，IRL都是这么干的）

Scheduled sampling(partially fed with its own synthetic data as prefix) is an inconsistent training strategy and fails to address the problem fundamentally.

SS算法会使训练结果一致性不好（？）。

1. GAN is designed for generating real-valued, continuous data but has difficulties in directly generating sequences of discrete tokens. The “slight change” makes little sense.
2. GAN can only give the score loss for an entire sequence when it has been generated.

GAN应用于序列生成时有两大缺点：

1. GAN的设计目的是生成连续的实数，它利用辨别模型给出的判断对生成模型做微小的工作，然而对于离散模型而言，这种微小的工作不足以使之从有限的字典空间里找到对应的生成；
2. GAN的辨别模型只能对完整的生成结果进行辨别。