MATLAB基础（五） 数据预处理

                                                                                      插值与拟合

插值与拟合的区别和联系

1、联系

    都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数的方法。

2、区别

    插值问题不一定得到近似函数的表达形式，仅通过插值方法找到未知点对应的值。数据拟合要求得到一个具体的近似函数的表达式。

插值方法

        选用不同类型的插值函数，逼近的效果就不同，一般有：

（1）最近邻算法插值（一维插值）

（2）拉格朗日插值算法（一维插值）

（3）双线性内插算法（二维插值）

（4）分段线性插值（二维插值）

（5）三次样条插值（二维插值）

（6）克里金插值（地理学）

（7）反距离权重插值算法（地理学）

 Matlab 实现：实现分段线性插值不需要编制函数程序，它自身提供了内部的功能函数

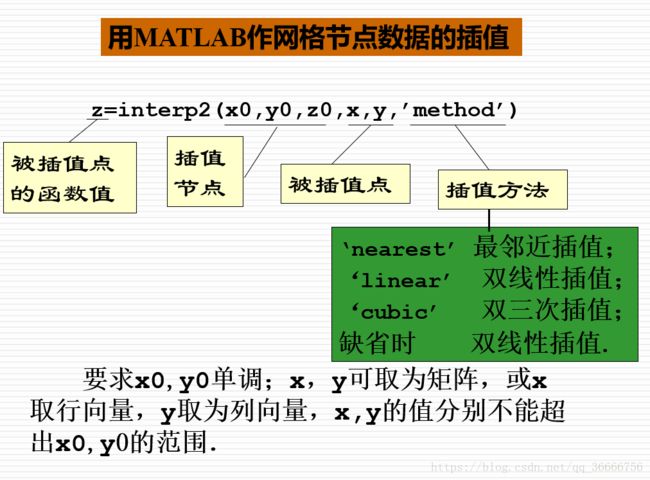
interp1(一维插值)

interp2(二维)

interp3(三维)

intern(n维)

例：从1点12点的11小时内，每隔1小时测量一次温度，测得的温度的数值依次为：5，8，9，15，25，29，31，30，22，25，27，24．试估计每隔1/10小时的温度值．

hours=1:12;

temps=[5 8 9 15 25 29 31 30 22 25 27 24];

h=1:0.1:12;

t=interp1(hours,temps,h,'spline');

plot(hours,temps,'+',h,t,hours,temps,'r:')     %作图

xlabel('Hour'),ylabel('Degrees Celsius’)

  1.先在三维坐标画出原始数据，画出粗糙的温度分布曲线图.

       输入以下命令：

         x=1:5;

         y=1:3;

        temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];

        mesh(x,y,temps)

2．以平滑数据,在 x、y方向上每隔0.2个单位的地方进行插值.

再输入以下命令:xi=1:0.2:5;yi=1:0.2:3;zi=interp2(x,y,temps,xi',yi,'cubic');mesh(xi,yi,zi)

画出插值后的温度分布曲面图.

 

 

 

 

 

    例 在某海域测得一些点(x,y)处的水深z由下表给出，船的吃水深度为5英尺，在矩形区域（75，200）×（-50，150）里的哪些地方船要避免进入．

1.输入插值基点数据  2.在矩形区域(75,200)×(-50,150)进行插值。 3. 作海底曲面图 4.作出水深小于5的海域范围,即z=5的等高线

%程序一：插值并作海底曲面图

 x  =[129.0  140.0  103.5  88.0  185.5  195.0  105.5 157.5  107.5  77.0  81.0  162.0  162.0  117.5 ];

y =[ 7.5  141.5  23.0  147.0  22.5  137.5  85.5      -6.5  -81  3.0  56.5  -66.5  84.0  -33.5 ];

z =[ 4  8  6  8  6  8  8  9  9  8  8  9  4  9 ];

x1=75:1:200;

y1=-50:1:150;

[x1,y1]=meshgrid(x1,y1);

z1=griddata(x,y,z,x1,y1,'v4');

meshc(x1,y1,z1)

 

%程序二：插值并作出水深小于5的海域范围。

x1=75:1:200;

y1=-50:1:150;

[x1,y1]=meshgrid(x1,y1);

z1=griddata(x,y,z,x1,y1,'v4');  %插值

z1(z1>=5)=nan;   %将水深大于5的置为nan，这样绘图就不会显示出来

meshc(x1,y1,z1)

水深小于5的海域范围 

 

                                                                              异常值处理

    异常值是数据集中偏离大部分数据的数据。从数据值上表现为：数据集中与平均值的偏差超过两倍标准差的数据，其中与平均值的偏差超过三倍标准差的数据，称为高度异常的异常值。

小波异常值提取

     信号的突变点和奇异点等不规则部分通常包含重要信息，一般信号的奇异性分为两种情况：

    （1）信号在某一时刻其幅值发生突变，引起信号的非连续，这种类型的突变称为第一类型的间断点；  

    （2）信号在外观上很光滑，幅值没有发生突变，但是信号的一阶微分有突变发生且一阶微分不连续，这种类型的突变称为第二类型的间断点。
     应用小波分析可以检测出信号中的突变点的位置、类型以及变化的幅度。

•（1）第一类型间断点的检测
    在本例中，信号的不连续是由于低频特征的正弦信号在后半部分突然有高频特征的正弦信号加入，首先利用傅里叶变换分析对信号在频域进行分析，发现无检测突变点，接着利用小波分析进行分析，结果证明它能够准确地检测出了信号幅值突变的位置，即高频信号加入的时间点。

 

load freqbrk;

x=freqbrk;%对信号进行傅里叶变换

f=fft(x,1024);

f=abs(f);

figure;

subplot(211);

 plot(x);

subplot(212);

plot(f);

  %使用db6小波进行6层

[c,l]=wavedec(x,6,’db6’);

figure(2);

subplot(811);

plot(x);

ylabel('x');

 %对分解的第六层低频系数进行重构

a=wrcoef('a',c,l,'db6',6); subplot(812);

  plot(a);

  ylabel('a6');
for i=1:6  %对分解的第6层到第1层的高频系数分别进行 d=wrcoef('d',c,l,'db6',7-i);
 subplot(8,1,i+2);
 plot(d);
 ylabel(['d',num2str(7-i)]);
end

 

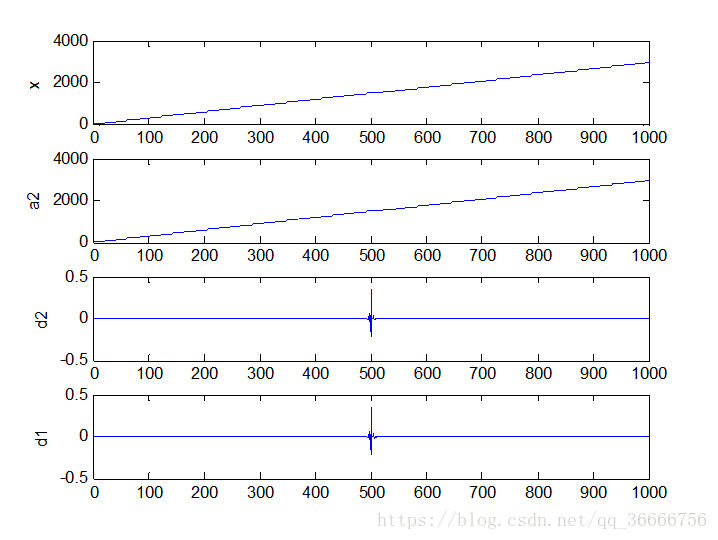
•    由两组图对比可以看出，由于傅里叶变换不具有时间分辨力，因此无法检测信号的间断点。而在小波分析的图中，在信号的小波分解的第一层高频系数d1和第二层高频系数d2中，可以非常清楚地观察到信号的不连续点，用db1小波比用db6小波要好。
     同时，这个例子也表明小波分析在检测信号的奇异点时具有傅里叶变换无法比拟的优越性，利用小波分析可以精确地检测出信号的突变点   经验第一类突变用db6小波分解 第二类db4小波分解

load nearbrk;

x=nearbrk;

%使用db4对信号进行2层分解

[c,l]=wavedec(x,2,‘db4’); 

subplot(411);

plot(x);

ylabel('x');

 %对分解的第六层低频系数进行重构

a=wrcoef('a',c,l,'db4',2);

subplot(412);     

plot(a);     

ylabel('a2');

for i=1:2               

 %对分解的第2层到第1层的高频系数进行重构
a=wrcoef('a',c,l,'db4',3-i);
subplot(4,1,i+2);
plot(d);
ylabel(['d',num2str(3-i)]);
 end

不足之处：

       小波变换是非平稳信号处理的有力工具，虽然小波变换有多种小波基函数可以供选择，但一旦小波基函数选定后，其特性就固定，各个尺度上的小波函数通过尺度和平移变换获得， 由于信号每分解一次，逼近信号和细节的长度减小一半。  在不同尺度上得到的逼近信号特征之间存在差异，小波变换时采用以个基函数导出的小波函数难以在不同尺度上准确地逼近局部信号特征，因此降噪预处理时的重构信号会丢失原有的时域特征。

                                                                             数据标准化

数据降维

•        主成分分析是一种通过降维技术把多个变量化为少数几个主成分(即综合变量)的多元统计方法，这些主成分能够反映原始变量的大部分信息，通过表示为原始变量的线性组合，为了使得这些主成分所包含的信息互不重叠，要求各主成分之间互不相关。主成分分析在很多领域都有广泛的应用，一般来说，当研究的问题涉及多个变量，并且变量间相关性明显，即包含的信息有所重叠时，可以考虑用主成分分析的方法，这样更容易抓住事物的主要矛盾，使问题简化。

Matlab函数

•(1)pcacov函数

• pcacov函数用来根据协方差矩阵或相关系数矩阵进行主成分分析，调用格式如下：

• COEFF=pcacov（V）

• [COEFF,latent]=pcacov（V）

• [COEFF,latent,explained]=pcacov（V）

•%调用pcacov函数根据相关系数矩阵作主成分分析

•% 返回主成分表达式的系数矩阵COEFF，返回相关系数矩阵的特征值向量latent和主成分贡献率向量explained

 

•2）princomp函数

• princomp函数用来根据样本观测值矩阵进行主成分分析，其调用格式如下：

•<1> [COEFF，SCORE]=princomp（X）

•<2> [COEFF,SCORE,latent]=princomp（X）

•<3> [COEFF,SCORE,latent,tsquare]=princomp（X）

•<4> [......]=princomp（X,‘econ’）

•       在指定服装标准的过程中，对128名成年男子的身材进行了测量，每人测量了六项指标：身高(x1)、坐高（x2）、胸围（x3）、手臂长（x4）、肋围（x5）和腰围（x6），样本相关系数矩阵如下表所示。根据样本相关系数矩阵进行组成分分析。

•（1）调用pcacov函数做主成分分析

•    %定义相关系数矩阵PHO

•         PHO = [1     0.79    0.36    0.76    0.25    0.51

•                      0.79  1       0.31    0.55    0.17    0.35

•                      0.36  0.31    1       0.35    0.64    0.58

•                      0.76  0.55    0.35    1       0.16    0.38

•                      0.25  0.17    0.64    0.16    1       0.63

•                      0.51  0.35    0.58    0.38    0.63    1

•                      ];

•[COEFF,latent,explained] = pcacov(PHO)

 

                                                                              数据的平滑处理

•一. smooth函数

•调用格式：

•yy = smooth(y)

•yy = smooth(y,span)

•yy = smooth(y,method)

•yy = smooth(y,span,method)

•yy = smooth(y,'sgolay',degree)

•yy = smooth(y,span,'sgolay',degree)

•yy = smooth(x,y,…)

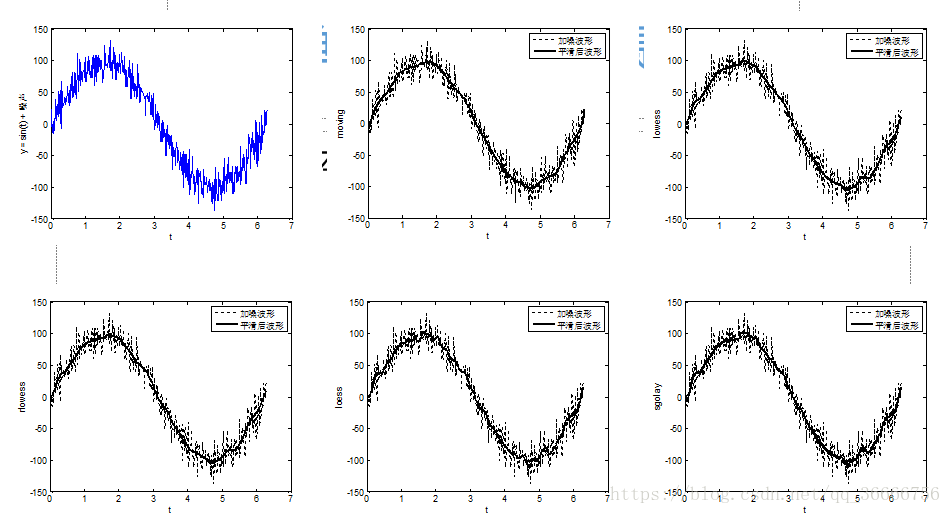
【例】产生一列正弦波信号，加入噪声信号，然后调用smooth函数对加入噪声的正弦波进行滤波（平滑处理）

 

n% 产生一个从0到2*pi的向量，长度为500

n>> t = linspace(0,2*pi,500)'; 

n>> y = 100*sin(t);  % 产生正弦波信号

n% 产生500行1列的服从N(0,152)分布的随机数，作为噪声信号

n>> noise = normrnd(0,15,500,1);

n>> y = y + noise;  % 将正弦波信号加入噪声信号

n>> figure;  % 新建一个图形窗口

n>> plot(t,y);  % 绘制加噪波形图

n>> xlabel('t');  % 为X轴加标签

n>> ylabel('y = sin(t) + 噪声');  % 为Y轴加标签

•移动平均法：

•>> yy1 = smooth(y,30);  % 利用移动平均法对y进行平滑处理

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on;

•>> plot(t,yy1,'k','linewidth',3);  % 绘制平滑后波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('moving');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');

•lowess方法：

•% 利用lowess方法对y进行平滑处理

•>> yy2 = smooth(y,30,'lowess'); 

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on;

•>> plot(t,yy2,'k','linewidth',3);  % 绘制平滑后波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('lowess');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');

•rlowess方法：

•% 利用rlowess方法对y进行平滑处理

•>> yy3 = smooth(y,30,'rlowess'); 

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on;

•>> plot(t,yy3,'k','linewidth',3);  % 绘制平滑后波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('rlowess');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');

•loess方法：

•% 利用loess方法对y进行平滑处理

•>> yy4 = smooth(y,30,'loess'); 

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on;

•>> plot(t,yy4,'k','linewidth',3);  % 绘制平滑后波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('loess');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');

•sgolay方法：

•% 利用sgolay方法对y进行平滑处理

•>> yy5 = smooth(y,30,'sgolay',3); 

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on;

•>> plot(t,yy5,'k','linewidth',3);  % 绘制平滑后波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('sgolay');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');

•二、smoothts函数

•调用格式：

•output = smoothts(input)

•output = smoothts(input, ‘b’, wsize)  % 盒子法

•output = smoothts(input, ‘g’, wsize, stdev) % 高斯窗方法

•output = smoothts(input, ‘e’, n)  % 指数法

•【例】现有上海股市日开盘价、最高价、最低价、收盘价、收益率等数据，时间跨度为2005年1月4日至2007年4月3日，共510组数据。完整数据保存在文件examp03_02.xls中，其中部分数据如下图所示。试调用smoothts函数对日收盘价数据进行平滑处理.

•

•绘制日收盘价曲线图：

•% 从文件examp03_02.xls中读取数据

•>> x = xlsread('examp03_02.xls'); 

•>> price = x(:,4)';  % 提取矩阵x的第4列数据，即收盘价数据

•>> figure;  % 新建一个图形窗口

•% 绘制日收盘价曲线图，黑色实线，线宽为2

•>> plot(price,'k','LineWidth',2); 

•% 为X轴和Y轴加标签

•>> xlabel('观测序号');

•>> ylabel('上海股市日收盘价');

•

•盒子法：

•% 用盒子法平滑数据，窗宽为30

•>> output1 = smoothts(price,'b',30); 

•% 用盒子法平滑数据，窗宽为100

•>> output2 = smoothts(price,'b',100); 

•>> figure;  % 新建一个图形窗口

•>> plot(price,'.');  % 绘制日收盘价散点图

•>> hold on

•% 绘制平滑后曲线图，黑色实线，线宽为2

•>> plot(output1,'k','LineWidth',2); 

•% 绘制平滑后曲线图，黑色点划线，线宽为2

•>> plot(output2,'k-.','LineWidth',2); 

•>> xlabel('观测序号'); ylabel('Box method'); % 为X轴和Y轴加标签

•% 为图形加标注框

•>> legend('原始散点','平滑曲线(窗宽30)','平滑曲线(窗宽100)','location','northwest');

•

•用高斯窗方法平滑数据：

•>> output3 = smoothts(price,'g',30);  % 窗宽为30，标准差为默认值0.65

•>> output4 = smoothts(price,'g',100,100);  % 窗宽为100，标准差为100

•>> figure;  % 新建一个图形窗口

•>> plot(price,'.');  % 绘制日收盘价散点图

•>> hold on

•% 绘制平滑后曲线图，黑色实线，线宽为2

•>> plot(output3,'k','LineWidth',2); 

•% 绘制平滑后曲线图，黑色点划线，线宽为2

•>> plot(output4,'k-.','LineWidth',2); 

•% 为X轴和Y轴加标签

•>> xlabel('观测序号'); ylabel('Gaussian window method');

•>> legend('原始散点','平滑曲线(窗宽30，标准差0.65)',...

•          '平滑曲线(窗宽100，标准差100)','location','northwest');

•用指数法平滑数据：

•>> output5 = smoothts(price,'e',30);  % 用指数法平滑数据，窗宽为30

•>> output6 = smoothts(price,'e',100);  % 用指数法平滑数据，窗宽为100

•>> figure;  % 新建一个图形窗口

•>> plot(price,'.');  % 绘制日收盘价散点图

•>> hold on

•% 绘制平滑后曲线图，黑色实线，线宽为2

•>> plot(output5,'k','LineWidth',2); 

•% 绘制平滑后曲线图，黑色点划线，线宽为2

•>> plot(output6,'k-.','LineWidth',2); 

•% 为X轴和Y轴加标签

•>> xlabel('观测序号'); ylabel('Exponential method');

•>> legend('原始散点','平滑曲线(窗宽30)','平滑曲线(窗宽100)','location','northwest');

•三、medfilt1函数（一维中值滤波）

•调用格式：

•y = medfilt1(x,n)

•y = medfilt1(x,n,blksz)

•y = medfilt1(x,n,blksz,dim)

•【例】产生一列正弦波信号，加入噪声信号，然后调用medfilt1函数对加入噪声的正弦波进行滤波（平滑处理）

•% 产生一个从0到2*pi的向量，长度为500

•>> t = linspace(0,2*pi,500)'; 

•>> y = 100*sin(t);  % 产生正弦波信号

•% 产生500行1列的服从N(0,152)分布的随机数，作为噪声信号

•>> noise = normrnd(0,15,500,1);

•>> y = y + noise;  % 将正弦波信号加入噪声信号

•>> figure;  % 新建一个图形窗口

•>> plot(t,y);  % 绘制加噪波形图

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('y = sin(t) + 噪声');  % 为Y轴加标签

•

•中值滤波：

•% 调用medfilt1对加噪正弦波信号y进行中值滤波，并绘制波形图

•>> yy = medfilt1(y,30);  % 指定窗宽为30，对y进行中值滤波

•>> figure;  % 新建一个图形窗口

•>> plot(t,y,'k:');  % 绘制加噪波形图

•>> hold on

•% 绘制平滑后曲线图，黑色实线，线宽为3

•>> plot(t,yy,'k','LineWidth',3); 

•>> xlabel('t');  % 为X轴加标签

•>> ylabel('中值滤波');  % 为Y轴加标签

•>> legend('加噪波形','平滑后波形');