C++ 二叉树常见用法
二叉树的创建:
上篇文章遍历的时候二叉树的创建是这样的:
TreeNode* T1 = new TreeNode(8);
TreeNode* T2 = new TreeNode(8);
TreeNode* T3 = new TreeNode(7);
TreeNode* T4 = new TreeNode(9);
TreeNode* T5 = new TreeNode(2);
TreeNode* T6 = new TreeNode(4);
TreeNode* T7 = new TreeNode(7);
T1->left = T2; T1->right = T3; T2->left = T4; T2->right = T5; T3->left = T6; T3->right = T7;
显然这种创建方式很繁琐,当二叉树分枝不多的情况下可以这样创建,但是复杂的时候我们就需要一种方便简洁的创建方式。之所以没有先讲二叉树的创建是因为创建方式依靠的背景不一样。还记得前序遍,中序遍历和后序遍历没。一般二叉树的创建是依靠遍历创建的。
我们依照前序遍历的准则创建二叉树:
创建的二叉树如下图所示,#代表为空,因为我们定义的是int型而不是char型,故下面的代码把#看成0输入为空。

下面代码用了两种构建方式:
第一种的前序遍历如图;
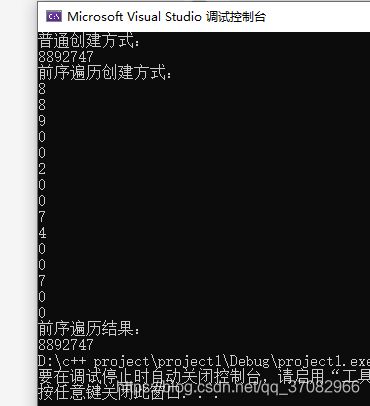
前序遍历的方式输入:889002007400700
#include
#include
using namespace std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int x):
data(x),left(NULL),right(NULL){}
};
void preprintftree(TreeNode* root) { //前序遍历
if (root) {
cout << root->data; // 打印根结点
preprintftree(root->left); // 前序遍历左子树
preprintftree(root->right); // 前序遍历右子树
}
else
root = NULL;
}
void preCreateTree(TreeNode* &T) // 前序遍历创建二叉树,需要注意* &T目的是让传递进来的指针发生改变
{
int data;
cin >> data;
if (data == 0)
{
T = nullptr;
}
else
{
T = new TreeNode(data); //构造结点
preCreateTree(T->left); //递归创建左子树
preCreateTree(T->right); //递归创建右子树
}
}
int main()
{
TreeNode* T1 = new TreeNode(8);
TreeNode* T2 = new TreeNode(8);
TreeNode* T3 = new TreeNode(7);
TreeNode* T4 = new TreeNode(9);
TreeNode* T5 = new TreeNode(2);
TreeNode* T6 = new TreeNode(4);
TreeNode* T7 = new TreeNode(7);
T1->left = T2; T1->right = T3; T2->left = T4; T2->right = T5; T3->left = T6; T3->right = T7;
cout << "普通创建方式:" << endl;
preprintftree(T1);
cout << endl;
TreeNode* Tree=nullptr;
cout << "前序遍历创建方式:" << endl;
preCreateTree(Tree);
cout << "前序遍历结果:" << endl;
preprintftree(Tree);
return 0;
}
二叉树的重建
二叉树的创建讲完了,下面介绍二叉树的重建:
先了解:
已知前序遍历和中序遍历可以确定唯一的二叉树;
已知后序遍历和中序遍历可以确定唯一的二叉树;
但是已知前序和后序不能确定。
已知二叉树的前序和中序,重建二叉树:
前序为:{ 1,2,4,7,3,5,6,8 }
中序为:{ 4,7,2,1,5,3,8,6 }
解题思路:
先序遍历规则:根节点==》左子树==》右子树
中序遍历规则:左子树==》根节点==》右子树
分析题目可知,二叉树中的节点值均是唯一的,不存在重复值。所以,
我们可以利用二叉树先序遍历和中序遍历特点,完成如下的工作:
Step1:确定根节点,即先序遍历preorder中的首个节点;
Step2:在中序遍历inorder中找到根节点的索引值index,以此为界,将中序遍历序列划分为
【左子树,根节点,右子树】,其中,左子树为索引值0至index,即inorder[0:index],
右子树为index+1至中序遍历末尾元素,即inorder[index+1:];
Step3:根据中序遍历序列中左右子树的节点数量,将先序遍历序列划分为【根节点,左子树,右子树】,
其中,左子树为索引值1至index+1,即preorder[1:index+1],
右子树为index+1至先序遍历末尾元素,即preorder[index+1:];
Step4:分别利用先序遍历和中序遍历中的左子树递归构造二叉树的左子树,
先序遍历和中序遍历中的右子树递归构造二叉树的右子树
#include
#include
#include
using namespace std;
struct treeNode {
int data;
treeNode* left;
treeNode* right;
treeNode(int x) :
data(x),left(NULL), right(NULL) {}
};
treeNode* buildtree(vector& pre, vector& vin) {
if (pre.size() == 0 || vin.size() == 0) return nullptr;
int val = pre[0];
treeNode* root = new treeNode(val);
int index = 0;
for (int i =0; i preleft(pre.begin() + 1, pre.begin() + index+1);
vector vinleft(vin.begin() , vin.begin() + index);
vector preright(pre.begin() + index +1,pre.end());
vector vinright(vin.begin() + index +1,vin.end());
root->left = buildtree(preleft, vinleft);
root->right = buildtree(preright, vinright);
return root;
}
void postprintfTree(treeNode* root) {
if (root!=nullptr) {
postprintfTree(root->left);
postprintfTree(root->right);
cout << root->data;
}
else {
root = NULL;
}
}
int main()
{
vectorpre={ 1,2,4,7,3,5,6,8 };
vectorvin={ 4,7,2,1,5,3,8,6 };
treeNode* tree = buildtree(pre,vin);
postprintfTree(tree); // 后序打印结果
return 0;
}
判断二叉树是否为另一个二叉树的子树:
思路:
输入两个二叉树,判断其中的一个是否为另一个的子树:
1、首先设置标志位flag = false,因为一旦匹配成功flag就设为true,
剩下的代码不会执行,如果匹配不成功,默认返回false
2、递归思想,如果根节点相同则递归调用comparetree(),
如果根节点不相同,则判断tree1的左子树和tree2是否相同,
再判断右子树和tree2是否相同
3、注意null的条件,HasSubtree中,如果两棵树都不为空才进行判断,
comparetree中,如果Tree2为空,则说明第二棵树遍历完了,即匹配成功,
tree1为空有两种情况(1)如果tree1为空&&tree2不为空说明不匹配,
(2)如果tree1为空,tree2为空,说明匹配。
#include
using namespace std;
struct treeNode {
int data;
treeNode* left;
treeNode* right;
treeNode(int x):
data(x),left(NULL),right(NULL){}
};
bool comparetree(treeNode* s1, treeNode* s2) {
if (s2 == nullptr) return true;
if (s1 == nullptr) return false;
if (s1->data != s2->data) return false;
return comparetree(s1->left, s2->left) && comparetree(s1->right, s2->right);
}
bool HasSubtree(treeNode* root1, treeNode* root2)
{
bool flag = false;
if (root1 == nullptr || root2 == nullptr) return false;
if (root1->data == root2->data) flag = comparetree(root1,root2);
if (!flag) flag = HasSubtree(root1->left,root2);
if (!flag) flag = HasSubtree(root1->right, root2);
return flag;
}
void preprintftree(treeNode* root) {
if (root) {
cout << root->data;
preprintftree(root->left);
preprintftree(root->right);
}
else
root = NULL;
}
int main()
{
treeNode* t1 = new treeNode(8);
treeNode* t2 = new treeNode(8);
treeNode* t3 = new treeNode(7);
treeNode* t4 = new treeNode(9);
treeNode* t5 = new treeNode(2);
treeNode* t6 = new treeNode(4);
treeNode* t7 = new treeNode(7);
t1->left = t2; t1->right = t3; t2->left = t4; t2->right = t5; t3->left = t6; t3->right = t7;
treeNode* tt1 = new treeNode(8);
treeNode* tt2 = new treeNode(9);
treeNode* tt3 = new treeNode(2);
tt1->left = tt2; tt1->right = tt3;
preprintftree(t1);
cout << endl;
preprintftree(tt1);
cout << endl;
bool res = HasSubtree(t1, tt1);
cout << res << endl;
return 0;
}
二叉树的镜像
思路:左右分枝对换就行了;
TreeNode* Mirror(TreeNode* pRoot) {
if (pRoot == nullptr) return pRoot;
TreeNode* temp;
temp = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = temp;
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
}
总的代码:
#include
using namespace std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int x):
data(x),left(NULL),right(NULL){}
};
TreeNode* Mirror(TreeNode* pRoot) {
if (pRoot == nullptr) return pRoot;
TreeNode* temp;
temp = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = temp;
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
}
void preprintftree(TreeNode* root) {
if (root) {
cout << root->data;
preprintftree(root->left);
preprintftree(root->right);
}
else
root = NULL;
}
int main()
{
TreeNode* T1 = new TreeNode(8);
TreeNode* T2 = new TreeNode(8);
TreeNode* T3 = new TreeNode(7);
TreeNode* T4 = new TreeNode(9);
TreeNode* T5 = new TreeNode(2);
TreeNode* T6 = new TreeNode(4);
TreeNode* T7 = new TreeNode(7);
T1->left = T2; T1->right = T3; T2->left = T4; T2->right = T5; T3->left = T6; T3->right = T7;
preprintftree(T1);
cout << endl;
TreeNode* p = Mirror(T1);
preprintftree(p);
return 0;
}
判断二叉树是否对称
由于上面给出了很多二叉树的测试用例,下面介绍的功能函数直接放核心代码函数接口:
bool isSame(TreeNode* p1,TreeNode* p2)
{
if(p1==NULL&&p2!=NULL)return false;
if(p2==NULL&&p1!=NULL)return false;
if(p1==NULL&&p2==NULL)return true;
if(p1->val==p2->val)return isSame(p1->right,p2->left)
&& isSame(p1->left,p2->right);
else
return false;
}
bool isSymmetrical(TreeNode* pRoot)
{
if(pRoot==NULL)return true;
return isSame(pRoot->left,pRoot->right);
}
求二叉树的深度:
思路:
从跟节点出发, 查询左子树的深度 , 获取右子树的深度,比较一下,取大的,再加一 。就是整个二叉树的深度
递归的三个条件
边界条件:当前节点下,是否还有子节点,没有返回,有继续递归
递归前进段:当前节点下,还有子节点
递归返回段:当前节点下,没有子节点
int TreeDepth1(TreeNode pRoot)
{
if(pRoot == null){
return 0;
}
int left = TreeDepth1(pRoot.getLeft());
int right = TreeDepth1(pRoot.getRight());
return Math.max(left, right) + 1;
}
二叉树是否为平衡二叉树:
平衡二叉树的定义:如果二叉树的每个节点的左子树和右子树的深度不大于1,它就是平衡二叉树。
思路:
最直接的做法,遍历每个结点,借助一个获取树深度的递归函数,根据该结点的左右子树高度差判断是否平衡,然后递归地对左右子树进行判断。
public classSolution {
public boolean IsBalanced_Solution(TreeNode root) {
if(root == null) {
return true;
}
return Math.abs(maxDepth(root.left) - maxDepth(root.right)) <= 1 &&
IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
private int maxDepth(TreeNode root) {
if(root == null) {
return 0;
}
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
}
这种做法有很明显的问题,在判断上层结点的时候,会多次重复遍历下层结点,增加了不必要的开销。如果改为从下往上遍历,如果子树是平衡二叉树,则返回子树的高度;如果发现子树不是平衡二叉树,则直接停止遍历,这样至多只对每个结点访问一次。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
return getDepth(root) != -1;
}
private int getDepth(TreeNode root) {
if (root == null) return 0;
int left = getDepth(root.left);
if (left == -1) return -1;
int right = getDepth(root.right);
if (right == -1) return -1;
return Math.abs(left - right) > 1 ? -1 : 1 + Math.max(left, right);
}
}