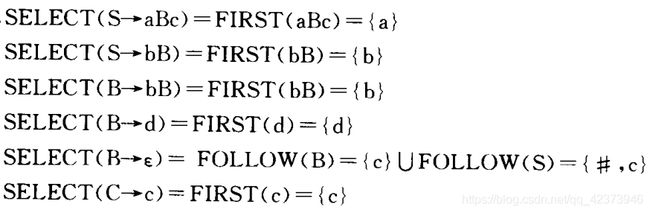编译原理课堂笔记之FIRST集,FOLLOW集与SELECT集等
编译原理课堂笔记之FIRST集,FOLLOW集与SELECT集等
- 各个集合的定义,求法,例题
- 1.FIRST集
- 1.1定义
- 1.2求解步骤
- 1.3例题
- 1.3.1例1
- 1.3.2例2
- 1.4简单小结
- 2.FOLLOW集
- 2.1定义
- 2.2求解步骤
- 2.3例题
- 2.3.1例1
- 2.3.2例2
- 2.4简单小结
- 3.SELECT集
- 3.1定义
- 3.2例题
- 3.2.1例1
- 3.2.2例2
- 4.FIRSTVT集和LASTVT集
- 4.1定义
- 4.2求解步骤
- 4.3例题
- 4.3.1例1
- 4.3.2例2
- 参考资料
各个集合的定义,求法,例题
这是我的第一篇课堂笔记,将记录我对于编译原理这门课一些知识点的理解,所写的笔记基于书本和其他人的博客。
1.FIRST集
1.1定义
设G=(VT,VN,P,S)是上下文无关文法 ,FIRST(x)={a|x能推导出ay,a∈VT,x,y∈V*}
特别的,x能够推出ε,则规定ε∈FIRST(x)。
事实上,FIRST(x)是指由符号串x出发,能够推导出的所有符号串中,处于串头的终结符号的集合
1.2求解步骤
以下都规定大写字母为非终结符,小写字母为终结符
1.若x∈VT,则FIRST(X)={x}。(简单讲,终结符的FIRST集就是它本身;例如:若X->a…,则将终结符a加入FIRST(X)中)
2.若X->ε ,则将终结符ε加入FIRST(X)中(ε表示空集);
3.若 X->BCD…G,则将First(B)所有元素(除了空集)加入First(x),现在需要做的就是检测B能不能推出ε:①若B不能推出ε,则结束了。②若能推出空集(ε),则将First(C)中所有元素(除了空集)加入First(A),然后再检测C能不能推出ε…一直循环这这两种判断,直到最后,若G之前的所有非终结符都能推出ε,将First(G)去除空集后的所有元素也加入First(A),若G也能推出ε,则将 ε加入First(A)。
对于上面第三步的理解:进行推导时(对于非终结符而言),非终结符中存在空串时,相当于你推到它的时候没做操作,直接推导到下一个符号即可。
例1:X->Ab (A中含有ε),那你要将FIRST(A)去除ε后的所有元素加入FIRST(X)中,并将终结符b加入FIRST(X)中。即:FIRST(X)=FIRST(A)- {ε}∪ {b}
例2:X->AB (A,B中都包含ε),那么FIRST(X)=FIRST(A)- {ε} ∪ FIRST(B)- {ε} U {ε}
1.3例题
1.3.1例1
设有文法G [S]:
S→AB|bC
A→ε|b
B→ε|aD
C→AD|b
D→aS|c
解法:
对于FIRST(S):FIRST(S)=FIRST(A)- {ε} U {b},检测A,因为A能推出ε,所以要将FIRST(B)- {ε}加入FIRST(S),继续检测B,它能推出ε,并且B是最后一个非终结符,所以最后一步要将{ε}加入FIRST(S),最后结果:FIRST(S)=FIRST(A)- {ε} U FIRST(B)- {ε} U {ε} U {b}
上述步骤需要先求解FIRST(A)和FIRST(B)
对于FIRST(A):FIRST(A)={ε,b}
对于FIRST(B):FIRST(B)={ε,a}
所以FIRST(S)={b} U {a} U {ε} U {b} ={b,a,ε}
对于FIRST(C)={b} U FIRST(A)- {ε},检测FIRST(A),它包含ε,所以要将FIRST(D)- {ε}加入FIRST(C),检测D,它不能推出ε,则最后不需要将{ε}加入FIRST(C)中,最后结果:FIRST(C)={b} U FIRST(A)- {ε} U FIRST(D),要先求出FIRST(D)
对于FIRST(D):FIRST(D)={a,c}
所以FIRST(C)={b} U {b} U {a,c}={a,b,c}
1.3.2例2
设有文法G [S]:
S→aAb
A→BA’
A’→dA|ε
B→e|ε
解法:
FIRST(S)={a}
FIRST(A)=FIRST(B)- {ε} U FIRST(A’)- {ε} U {ε} 因为B和A’都能推出ε且A’是最后一个非终结符
FIRST(A’)={d,ε}
FIRST(B)={e,ε}
所以FIRST(A)=FIRST(B)- {ε} U FIRST(A’)- {ε} U {ε} ={e} U {d} U {ε} = {e,d,ε}
1.4简单小结
1.对于终结符而言,FIRST集中的元素只有它本身
2.对于非终结符而言,如果开始符是终结符或者空符号串ε,则加入其FIRST集中;若开始符是非终结符,则要加入它的不含ε的FIRST集,并考虑其为ε时的情况。
2.FOLLOW集
2.1定义
设G=(VT,VN,S,P)是上下文无关文法,A∈VN,则
FOLLOW(A)={a|S→…Aa…,a∈VT}
特别的:S→…A,则规定#∈FOLLOW(A)
2.2求解步骤
事实上,FOLLOW(A)是指在文法G[S]的所有句型中,紧跟在非终结符A后的终结符号的集合。
1.对文法开始符号S,将{ # }加入FOLLOW(S)中;
2.对于产生式:A→aBC,将除去空集ε的First(C)加入Follow(B)中;
3.对于产生式:A→aB或者A→aBC,(其中C可以推导出ε,即C→ε)则将Follow(A)加入Follow(B)中。
2.3例题
2.3.1例1
设有文法G [E]:
E → TE’
E’ → +TE’ | ε
T → FT’
T’ → *FT’ | ε
F → (E) | i
解法:
先求出他们的FIRST集
FIRST(F)= { ( , i }
FIRST(T’)={ * , ε }
FIRST(T)=FIRST(F)- {ε}={ ( , i }
FIRST(E’)={ + , ε }
FIRST(E)=FIRST(T)={ ( , i }
FOLLOW集的求法:
对于FOLLOW(E),它是文法的开始,所以{#}加入FOLLOW(E),之后只看F → (E) | i,所以FOLLOW(E)={#} U { ) } = { #, ) }
对于FOLLOW(E’),看E → TE’ 和E’ → +TE’ | ε ,对于E → TE’这个式子FOLLOW(E’)= FOLLOW(E)= { #, ) } (E’在最后,对应步骤3),对于E’ → +TE’ | ε ,FOLLOW(E’)=FOLLOW(E’) 等于它本身,不做处理。即最后FOLLOW(E’)= { #, ) }
对于FOLLOW(T),看E → TE’和E’ → +TE’ | ε,对于E → TE’,FOLLOW(T)= FIRST(E’)- {ε} = { + },这里要注意的是E’→ε,转到步骤3,FOLLOW(E’)要加入FOLLOW(T),所以FOLLOW(T)= {+} U { #, ) }={ +, # , ) }
对于FOLLOW(T’),看T → FT’和T’ → *FT’ | ε;对于T → FT’,符合步骤3,将FOLLOW(T)加入 FOLLOW(T’),所以FOLLOW(T’)= FOLLOW(T)={ +, # , ) };对于T’ → *FT’ | ε,本身的FOLLOW集加入本身,不用管,最后FOLLOW(T’)={ +, # , ) }
对于FOLLOW(F),看T → FT’和T’ → *FT’ | ε;对于T → FT’,将FIRST(T’)- {ε} 加入FOLLOW(F),别忘了检测T’能不能推出ε(能),所以这里还要FOLLOW(T)加入FOLLOW(F);对于这个式子T’ → *FT’ | ε,本身加入本身,没意义,不管它,所以最后FOLLOW(F)= FIRST(T’)- {ε} U FOLLOW(T) = { * } U { +, # , ) } = { * ,+, # , ) }
2.3.2例2
设有文法G [S]:
S→aAb
A→BA’
A’→dA|ε
B→e|ε
先给出FIRST集
FIRST(S)={a}
FIRST(A’)={d,ε}
FIRST(B)={e,ε}
FIRST(A)= {e,d,ε}
对应的FOLLOW集
FOLLOW(S)= { # }
FOLLOW(A)= {b} U FOLLOW(A’) = { b }
FOLLOW(A’) = FOLLOW(A)={ b }
FOLLOW(B)= FIRST(A’)- {ε} U FOLLOW(A)={ d } U {b}={ d ,b}
2.4简单小结
FOLLOW集对于非终结符而言,是非终结符的全部后跟符号的集合,如果后跟终结符则加入,如果后跟非终结符,则加入该非终结符的不含空符号串的FIRST集,特别地,文法的识别符的FOLLOW集需要额外的加入‘#’。
3.SELECT集
3.1定义
设文法G=(VT,VN,P,S),规则A→x∈P,则
SELECT(A→x)=
{
FIRST(x),当x!=ε
FOLLOW(A),当x=ε
}
若x不能推导出ε,则SELECT(A→x)=FIRST(x)
如果α能推导出ε则:SELECT(A→x)=(FIRST(x) –{ε})∪FOLLOW(A)
3.2例题
3.2.1例1
设有文法G [S]:
S→AB|bC
A→ε|b
B→ε|aD
C→AD|b
D→aS|c
SELECT(S→AB)=(FIRST(AB)-{ε})∪FOLLOW(S)={b,a,#} SELECT(S→bC)=FIRST(bC)={b}
SELECT(A→ε)=(FIRST(ε) -{ε})∪FOLLOW(A)={a,c,#}
SELECT(A→b)=FIRST(b)={b}
SELECT(B→ε)=(FIRST(ε) -{ε})∪FOLLOW(B)={#}
SELECT(B→aD)=FIRST(aD)={a}
SELECT(C→AD)=FIRST(AD)={a,b,c}
SELECT(C→b)=FIRST(b)={b}
SELECT(D→aS)=FIRST(aS)={a}
SELECT(D→c)=FIRST( c )={c}
3.2.2例2
设有文法G [S]:
S→aAb
A→BA’
A’→dA|ε
B→e|ε
先给出FIRST集
FIRST(S)={a}
FIRST(A’)={d,ε}
FIRST(B)={e,ε}
FIRST(A)= {e,d,ε}
对应的FOLLOW集
FOLLOW(S)= { # }
FOLLOW(A)= { b }
FOLLOW(A’) ={ b }
FOLLOW(B)= { d ,b}
4.FIRSTVT集和LASTVT集
4.1定义
4.2求解步骤
4.3例题
4.3.1例1
4.3.2例2
参考资料
1.https://blog.csdn.net/zheng__jun/article/details/52684612#commentBox
2.http://blog.sina.com.cn/s/blog_92d6d632010154xi.html
3.《编译技术·重庆大学出版社》