线性代数基础1--方程组的求解过程

我们一般所讲的方程不是指恒等式，而是一种条件等式； 例如x+1 =1+x 是恒等式，方程的解是任意的数；这就不是通常意义上的方程了，当然，其实恒等式是一种特殊的方程；

而例如x+1 = 2就是我们通常所说的方程，它是在某些特殊值的情况下才有解的；

我们来看看数学上严格的定义吧：

线性方程组：

         n个未知数X1,X2, ..., Xn的如下形式的方程:

               a1x1 + a2X2+ ... anXn = b        方程1

称为n元一次方程，也称为n元线性方程(linear equation in n variables), 其中一次项系数a1,a2,...,an和常数项b都是已知数;

         如果c1,c2, ...,cn是n个数，并且当X1 = c1, X2 = c2, ..., Xn=cn代入方程1能使方程变为等式，则这组数(c1,c2, ...,cn)称为方程的一个解(Solution)；这组数组中第i个数ci称为解的第i个分量；

当这样的方程不是一个，而是有多个时，我们就得到的n元线性方程组(linear equations in n variables)及这个方程组的解(solution).

如下图：

举个例子：

     看下面的一个四元一次线性方程组：

        X1+2*X2+3*X3+4*X4 = -3                       1式

        X1+2*X2+0*X3-5*X4  = 1                        2式

        3*X1-X2-X3+0*X4      =  1                       3式

        X1+0*X2+X3+2*X4    = -1                       4式

根据我们的定义，这就是一个n元(这里n=4)的线性方程组；

可以使用Python程序计算出结果：

## 先确定常数项
A1 = [[1, 2, 3, 4],
      [1, 2, 0, -5],
      [3, -1, -1, 0],
      [1, 0, 1, 2]]
A = np.array(A1)
# 确定等式右边的值
B = np.array([-3,
              1,
              1,
              -1])

# 计算方程组的解
try:
    c = solve(A,B)
    print(c)   
except:
    print("Matrix is singular.")

# [ 0.08333333 -0.16666667 -0.58333333 -0.25      ]

我们发现，用Python程序求解过程的过程很简单，只要套用一定的函数调用就可以，但是事实上这组解是一组近似解。

我们可以用纯数学的方法来求解一次：

具体来说就是首先将一个方程变成一个向量，将线性方程组变成矩阵(向量组)表示，

        X1+2*X2+3*X3+4*X4 = -3                       ==》   1   2    3   4     -3

        X1+2*X2+0*X3-5*X4  = 1                        ==》   1   2    0   -5     1  

        3*X1-X2-X3+0*X4      =  1                       ==》   3  -1   -1    0     1

        X1+0*X2+X3+2*X4    = -1                       ==》   1   0     1    2    -1

这样，我们把原来方程的表示方法大大简化了，大家不要小看这种简化。数学上的这种简化，有时会带来意想不到的好处。

它有助于我们只面问题的本质，而去掉烦琐末节的不重要的信息。在数学的发展种，这种方法有着深刻的影响。

然后使用初等行变换(elementary transformation of rows)将矩阵化解成一种阶梯型(echelon)矩阵（不知道什么是阶梯型矩阵吗，请查百度）的方式来处理。

注意初等行变换包括以下几种：

A -(i,j)-》 B  将矩阵A某两行i,j互换位置；                        变换1

A -a(i)-》B  将某行i乘以某个非0的数a；                         变换2

A-a(i)+j-》B 将某行i乘以某个非0的数a加到零一行j；     变换3

这三种变换(线性组合)属于同解变换，这样可以产生一个新的方程组，也就是说这些变换不会产生增根（并不满足方程的解而增加出来的解）。

1   2   3     4    -3                              

1   2   0     -5    1

3  -1  -1     0     1

1   0   1      2    -1     使用变换3-- 1式*-1+2式，1式*-3+3式，1式*-1+4式-->    1   2     3      4      -3

                                                                                                                          0   0     -3     -9     4

                                                                                                                         0  -7    -10   -12   10

                                                                                                                         0  -2     -2    -2      2

使用变换2-- 2式<-换位->4式，-->         1   2   3    4    -3

                                                              0  -2  -2    -2    2

                                                              0  -7 -10   -12  10

                                                              0  0   -3    -9   4

使用变换2， 2式/2； 使用变换3，2式*-7+3式，  ->  1   2    3    4      -3

                                                                                   0   -1   -1  -1      1

                                                                                   0   0    -3  -5      3

                                                                                   0   0    -3   -9     4

使用变换2，2式*-1；使用变换3，3式*-1+4式，   -> 1   2    3    4     -3

                                                                                   0   1    1    1     -1

                                                                                   0    0   -3  -5    3

                                                                                   0    0    0   -4   1

其实，变换到这里，已经可以求出x4 = -4/1，这样再回代，也可以求出x1,x2,和x3的值；

也可以继续化解下去，得到：

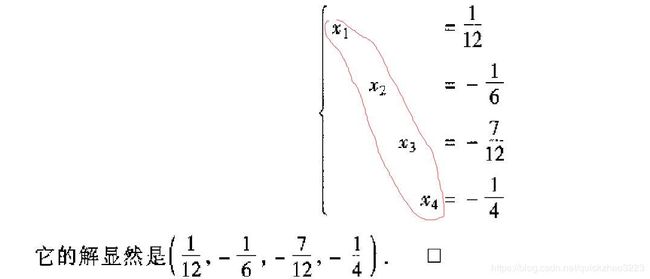
从而，我们可以得出方程组的解集：

 

 这是用数学方法得到的精确解，之前我们用Python算出来的是近似解[ 0.08333333 -0.16666667 -0.58333333 -0.25      ]。

我们再来看一个例子：

                                                                           

最后把这个矩阵解释回方程组的形式，可以得到：

        x1 + 2*x2 - 5*x4 = 1

        x3+3*x4     = -4/3

==>  x1 = 1-2*x2+5*x4

        x3  = -4/3-3*x4

这里等号右边的未知数x2，x4可任取值；我们可以给x2取定一个任意值t1，给x4取定一个任意值t2，

则x1，x3的值，可以表示成x2和x4值的形式，这样，我们也可以将方程组的解集表示成如下的集合形式：

{(1-2*t1+5*t2, t1, -4/3-3*t2, t2) | t1, t2可以在允许的范围内任意取值；注意：这里的范围可能要根据具体情况，一般是有理数，实数或者复数范围}

注意这里的集合解我们称为方程组的通解(general solutions), 当其中独立参数t1,t2取遍允许范围所有可能的值时，就得到方程组的所有解；当t1，t2取定一组具体的值时，就得到方程组的一个解，称为特解(special solution).

其实，通解也可以表达成下面的形式：

x1          1-2*x2+5*x4                         -2                  5            1

x2     =   x2                            =   x2 *  1     +   x4 *  0        +   0

x3         -4/3 - 3*x4                              0                  -3          -4/3

x4         x4                                           0                  1            0

注意， 这里的(-2,1,0,0),(5,0,-3,1),x2,x4在线性代数里面有其特别的含义。我们下次再聊。

总结：我们这里简单讲解了线性方程组的矩阵变换（矩阵的同解变换--》阶梯形矩阵）解法，我们也演示了Python种代码的求解过程，但是，这个解有时不够精确。计算机种怎么得到尽可能精确的解，属于计算数学讨论的范畴，我们这里不在讨论。

我们下次再回到几何观点来看待线性代数。

 

参考：《线性代数》李尚志编著