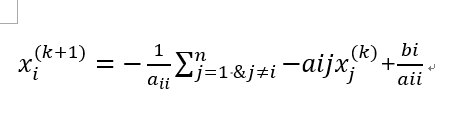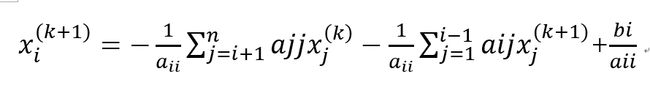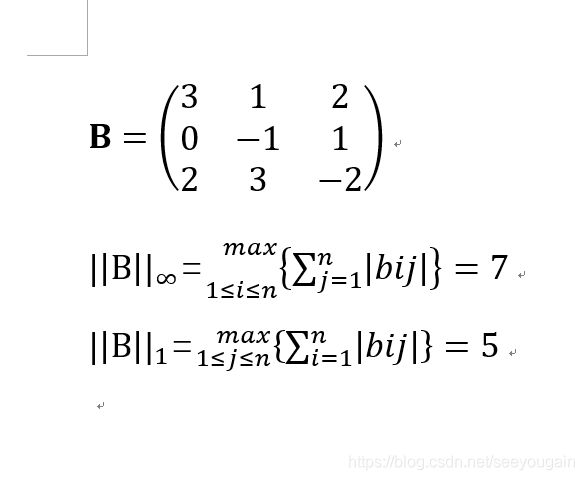线性方程组的迭代法
数值分析——方程组求根
- 1.问题
- 2.Jocobi方式迭代
- 2.1方程组表示
- 2.2 矩阵表示
- 2.3分量表示
- 3.Gauss-Seidel迭代法
- 3.1方程组表示
- 3.2矩阵表示
- 3.3分量表示
- 4.相关知识的引入——范数
- 5.具体题目的解答
- 5.1题目
- 5.2程序
- 5.2.1Jacobi迭代法
- 5.2.1推广到x有n个元素
- 5.2.2Gauss-Seidel迭代法
- 5.3.1推广到x有n个元素
1.问题
AX=B
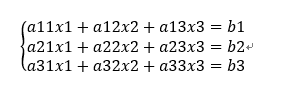
A=[a11,a12,a13;a21,a22,a23;a31,a32,a33]
U=[0,a12,a13;0,0,a23;0,0,0]
D=[a11,0,0;0,a22,0;0,0,a33]
L=[0,0,0;a21,0,0;a31,a32,0]
A=U+D+L
b=[b1;b2;b3]
2.Jocobi方式迭代
2.1方程组表示
-
分离变量
a11x1=-a12x2+a13x3+b1
a22x2=-a21x1-a23x3+b2
a33x3=-a31x1-a32x2+b3 -
系数化为1
x1=(-a12x2+a13x3)/a11+b1/a11
x2=(-a21x1-a23x3)/a22+b2/a22
x3=(-a31x1-a32x2)/a33+b3/a33x=Bx+f(x加粗表示向量)
x=(x1;x2;x3)
B=(0,-a12/a11,-a13/a11;-a21/a22,0,-a23/a22;-a31/a33,-a32/33,0);
f=(b1/a11;b2/a22;b3/a33) -
构造迭代格式
x(k+1)=B x(k)+f
2.2 矩阵表示
- 分离
DX=-(U+L)X+b - 系数
X=(-(U+L)X+b)/D
X=BX+f
B=(-(U+L)X)/D
f=b/D - 迭代
X(k+1)=BX(k)+f
2.3分量表示
赋初值:x(0)=(0;0;0)
3.Gauss-Seidel迭代法
使用之前计算得出的值替代,使得计算次数大大缩小
3.1方程组表示
x1(k+1)=(-a12x2(k)+a13x3(k))/a11+b1/a11
x2(k+1)=(-a21x1(k+1)-a23x3(k)/a22+b2/a22
x3(k+1)=(-a31x1(k+1)-a32x2(k+1))/a33+b3/a33
3.2矩阵表示
- step1
(L+D)X=-UX+b - step2
X=-UX/(L+D)+b/(L+D)
X=BX+f
B=-U/(L+D)
f=b/(L+D) - step3
X(k+1)=BX(k)+f
3.3分量表示
4.相关知识的引入——范数
5.具体题目的解答
5.1题目
5.2程序
5.2.1Jacobi迭代法
A=[5,2,1;-1,4,2;2,-3,10];
b=[-12;20;3];
x1(1)=0;
x2(1)=0;
x3(1)=0;
x1(2)=(-A(1,2)*x2(1)-A(1,3)*x3(1))/A(1,1)+b(1)/A(1,1);
x2(2)=(-A(2,1)*x1(1)-A(2,3)*x3(1))/A(2,2)+b(2)/A(2,2);
x3(2)=(-A(3,1)*x1(1)-A(3,2)*x2(1))/A(3,3)+b(3)/A(3,3);
i=2;
y=[x1;x2;x3];
t=[abs(y(1,2)-y(1,1));abs(y(2,2)-y(2,1));abs(y(3,2)-y(3,1))];
while(max(t)>0.0005)
x1(i+1)=(-A(1,2)*x2(i)-A(1,3)*x3(i))/A(1,1)+b(1)/A(1,1);
x2(i+1)=(-A(2,1)*x1(i)-A(2,3)*x3(i))/A(2,2)+b(2)/A(2,2);
x3(i+1)=(-A(3,1)*x1(i)-A(3,2)*x2(i))/A(3,3)+b(3)/A(3,3);
y=[x1;x2;x3];
t=[abs(y(1,i+1)-y(1,i));abs(y(2,i+1)-y(2,i));abs(y(3,i+1)-y(3,i))];
i=i+1;
end
5.2.1推广到x有n个元素
需要注意的是x(i,j)中的i代表x1,x2…;j代表迭代的次数
A=input('请输入A矩阵:A=');
b=input('请输入B矩阵:B=');
n=length(b);
m=1;
for i=1:n
x(i,1)=0;
end
while(1==1)
for i=1:n
t=0;
for j=1:n
if(j~=i)
t=t+x(j,m)*A(i,j);
end
end
x(i,m+1)=b(i)/A(i,i)-t/A(i,i);
end
y=x(:,m+1)-x(:,m);
m=m+1;
if(max(y)<0.00001)
break;
end
end
5.2.2Gauss-Seidel迭代法
A=[5,2,1;-1,4,2;2,-3,10];
b=[-12;20;3];
x1(1)=0;
x2(1)=0;
x3(1)=0;
x1(2)=(-A(1,2)*x2(1)-A(1,3)*x3(1))/A(1,1)+b(1)/A(1,1);
x2(2)=(-A(2,1)*x1(2)-A(2,3)*x3(1))/A(2,2)+b(2)/A(2,2);
x3(2)=(-A(3,1)*x1(2)-A(3,2)*x2(2))/A(3,3)+b(3)/A(3,3);
i=2;
y=[x1;x2;x3];
t=[abs(y(1,2)-y(1,1));abs(y(2,2)-y(2,1));abs(y(3,2)-y(3,1))];
while(max(t)>0.0005)
x1(i+1)=(-A(1,2)*x2(i)-A(1,3)*x3(i))/A(1,1)+b(1)/A(1,1);
x2(i+1)=(-A(2,1)*x1(i+1)-A(2,3)*x3(i))/A(2,2)+b(2)/A(2,2);
x3(i+1)=(-A(3,1)*x1(i+1)-A(3,2)*x2(i+1))/A(3,3)+b(3)/A(3,3);
y=[x1;x2;x3];
t=[abs(y(1,i+1)-y(1,i));abs(y(2,i+1)-y(2,i));abs(y(3,i+1)-y(3,i))];
i=i+1;
end
5.3.1推广到x有n个元素
略