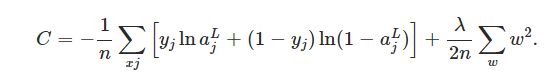依然是Michael Nielsen的书,依然是神经网络,上文说到的是神经网络有关于损失函数的调整使得学习速度加快,但是还是有几个问题没有解决:
- 过拟合问题
- 权重和b初始化问题
一,首先来看第一个问题:过拟合(overfitting)
什么是overfitting,我这个人不是典型的学院派,所以正儿八经的定义也不会用,用我的话说就是学习过度,主要表现在两个方面:第一,在现有的训练数据上模型已经不能更加优化了,但是整个学习过程仍然在学习;第二,对于局部数据噪声(noise)学习过度,导致模“颠簸”(这个词是我自创的),所谓对局部噪声学习过度表现在对于给定的训练数据,模型过度学习了局部的噪声,而这些噪声对于模型的泛化(generalization)并没有实际用处。
来看下具体的过度学习的例子:
1)在现有数据下学习过度:
还是以前面文章所说的图片识别的例子为例,我们建立784*30*10的神经网络模型,但是在本例中我们使用训练数据将不是之前的50000个数据,而是50000个数据中的10000个数据,使用的步长为0.5,我们看下其在测试数据的表现:
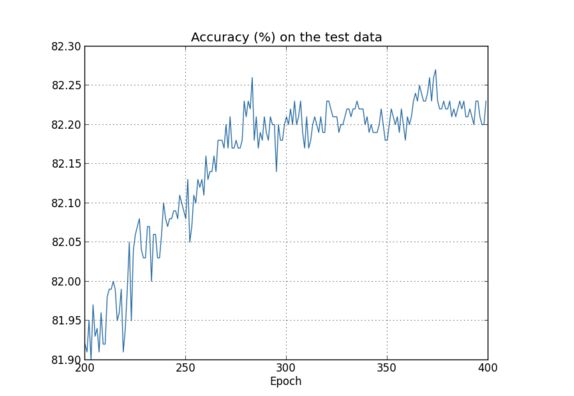
可以看到,对于测试数据的准确性在打了约280代左右的时候达到峰值,之后的训练对准确率的提高并没有实际的提高,因此在280代以后的数据训练,我们可以称之为overfitting
2)局部噪声学习过度,导致模型颠簸
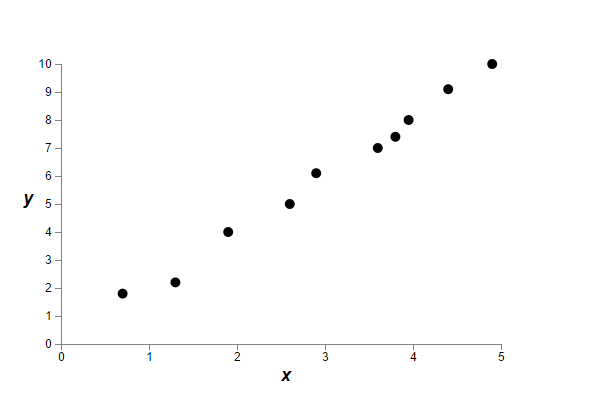
这个问题可以用回归问题作为典型的例子,看下面的数据:
我们对上面的数据进行回归分析,有多种拟合方法,考虑最简单的两种,一是线性回归,二是多项式回归
使用线性回归的话,我们得到的可能是y=2*x,如下图:
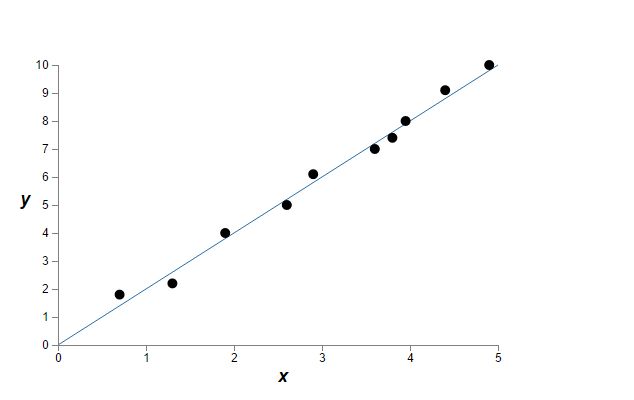
使用多项式拟合y=a0+a1*x+a2*x^2+...+a9*x^9,我们可能看到如下结果:

对于给定的数据点,我们无法确定哪一种拟合方法是对的,但是对于一般模型而言,我们往往认为简单的参数模型具有更大的普适性(书中并没有给出实质意义上的证明),不去争论这句话的正确性,暂且认为这种假设是对的,也就是说我们认可上面的y=2x的结果,如此一来,我们就认为多项式拟合是overfitting,其过度学习到了数据的局部噪音,而这些局部噪音对整个模型的一般性没有用。
以上两个例子可以通俗的解释过拟合现象,那么问题来了,我们如何解决上述的两个过拟合问题。
【1】对于第一个过拟合问题,也就是参数学习过程过多,我们在之前的training data和test data之外,又引入了新的数据集validate data,validate的数据集与training data和test data都是不一样的,validate 的主要作用是防止训练过度。
我们来看一下validate数据是怎么发挥作用的:
其实很简单,在模型每一代训练出的模型的时候,使用validate data计算正确率,一旦该正确率不在出现明显变化的时候就需要停止训练了。
。另外,训练数据越多,出现过拟合的现象会越少,所以扩大训练数据集也是解决过拟合的一个办法。
【2】对于第二个过拟合问题,解决方法是引入规则化(Regularization)机制
什么是规则化,其实也很简单,对于损失函数是交叉熵的神经网络,那么其损失函数变换成下面的形式:
式子加号 后面的表达式就是规则化(Regularization),那么对于使用平方损失函数,其形式也是一样的:

其实从式子中可以看出,加入规则化因子之后,整个模型其实是奔着选取较小的w而进化的,因为如果需要损失函数值小的话,一旦选取了比较大的w,那么只有等式右边第一项式子的值比较小的情况下才行,因此规则化的目的其实是减轻比较大的w值对损失函数的影响,为什么需要这么做,我们假设对于线性回归而言,有一个数据特别偏离主模型,这样的话,往往会导致模型受这个影响比较大,从而偏离主模型,这时候就需要抵消这个数据对结果的影响,这就用到了规范化,目的是消除其某些损失函数值过大的点影响,对于神经网络,正则化的目的是为了消除太大的W对结果的影响,其结果就是局部的变化因素(个别w的变化)不会影响整个模型的数据,只有对全部模型起变化的因素才能影响到模型的建立,这样就消除了局部噪声的影响。
当加入规则化因子之后,对于w和b求导的并没有什么实质性的变化,与之对应的代码也不用做太多修改:
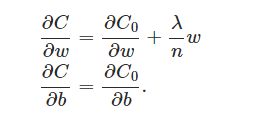
然后让我们看一下使用了规范因子之后的结果,以之前的训练数据为例,训练集:50000个,测试集:10000个,步长为5:
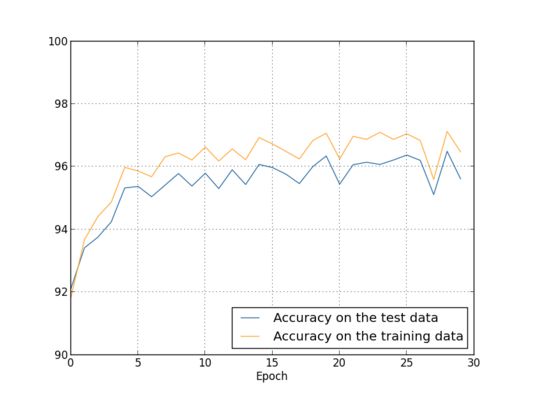
规范化以后的正确率最好是在96.49%左右,比没有使用规则化的95。49%还是提高了不少。
需要说明的是规范化因子的lambda是一个大于0的度量值,如果lambda比较大的话那么就是说明模型倾向更小的权重,当lambda比较小的时候说明模型倾向大的权重,所以lambda算是一个平衡值,而这个平衡值往往需要通过实验确定比较好的值。
当然规范化还有很多方法,上面的方法称之为L2规范化,也叫权重衰减规范化还有一些比较主流的正则化方法,如L1正则化、Dropout正则化,数据集拓展方法,详情可以见,正则化方法一文,有较详细的解释,这里就不一一解释。
二,然后来看第二个问题:权重初始化问题
回忆之前使用的初始化权重方法,我们是按照标准为1,均值为0的高斯分布随机生成数据集,但是这个会存在一些问题,以有1000个输入的单个神经元而言,我们假设输入的1000个数的500个为0,500个为1,w和b均服从(0,1)的高斯分布,那么对于z=w*x+b的输出,其服从标准差为sqrt(501)=22.4,均值为0的高斯分布, 其图像是:

这上面会有很多的远大于1和远小于-1的值,一旦选择了这些值,由于这些值比较大,因此可能导致最终的输出结果接近0或者接近1,从而在梯度下降过程中改变值非常小,从而导致训练速度减缓。
按照上面的想法,其实我们是想要w的值尽量分布在(-1,1)之间,但是我们看到高斯分布符合一个规律:标准差越小,分布曲线越尖,标准差越大越扁平,因此我们需要根据数据集修正其标准差即可。
因此,我们有了新的初始化高斯分布:
对于有N个w值的神经元,我们将每个w初始化为服从(0,sqrt(n))高斯分布的值,但是b不变,还是服从(0,1)高斯分布,那么对于上个问题,其输出z=w*x+b就服从(0,sqrt(3/2))的高斯分布,因为其方差等于:1/1000 * 500+1=3/2.,其图像为:
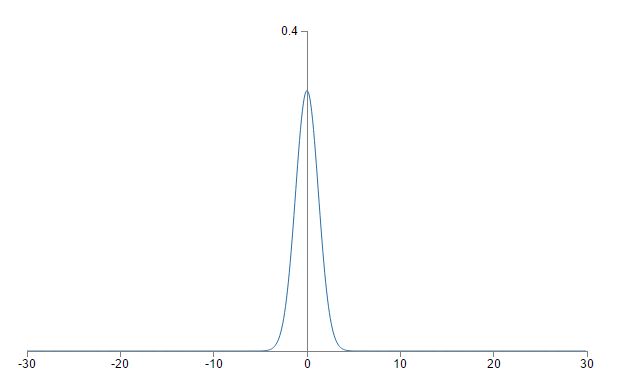
可以看到,其分布就会集中在0附近,因此不会导致输出的值z过大从而引起学习速度减慢的结果。
这里需要说明的是之所以选择b仍然服从(0,1)高斯分布是因为b的选取对最终结果并没有实质性的影响,因此b的可以选择0也可以选择其他的值,这里是选择服从(0,1)高斯分布。
这就是神经网络的调参过程。