深度学习笔记: 逻辑回归模型和二元分类
多元分类(classification)
在机器学习中,多元分类 是将示例归类为多个(大于两个)类别中的一类(将示例归为两类中的一类被称为二元分类)。
一些分类算法自然地允许使用超过两类,另一些自然是二元分类算法;然而,它们可以通过多种策略转化为多元分类。
多元分类不应该和多标签分类相混淆,多标签分类要为每个示例预测多个标签,即一个示例可以同时被归为多个类别。
所以,要解决多元分类问题,只需将其简化为多个二元分类问题。
而顾名思义,二元分类就是给定一个对象 x \mathit{x} x,根据标签给它划分为A类还是B类
逻辑回归(Logistic regression)
逻辑回归就是一种解决二分类问题的机器学习方法,说到逻辑回归,就不得不提到线性回归,逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。
线性回归
线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。
线性回归分析用于研究一个变量与另一个变量或多个变量之间的关系。
以双变量为例,变量X和变量Y之间可以有三种关系:正线性相关、负线性相关、不是线性相关(随机)。
线性回归的表达式如下:
f ( x ) = w T x + b f(\bm{x}) = \bm{w}^T\bm{x} + b f(x)=wTx+b
线性回归对于给定的输入 x \bm{x} x ,输出的是一个数值 y ,因此它是一个解决回归问题的模型。也就是说,我们能通过线性回归,知道x和某个特征的相关度。
但是对于二分类问题,我们需要的结果并不是数值,而是0 or 1这样能够给对象分类的布尔值,如何能解决这个问题呢?
一个常用的解决方法是设置一个阈值,大于这个阈值,则分为A类,小于则分为B类
采用这种方法的模型又叫做感知机(Perceptron)。
而另一个方法就是不去直接预测标签,而是去预测标签为A概率,我们知道概率是一个[0,1]区间的连续数值,那我们的输出的数值就是标签为A的概率。一般的如果标签为A的概率大于0.5,我们就认为它是A类,否则就是B类。这就是逻辑回归 (Logistics Regression)。
逻辑回归 (Logistics Regression)
我们知道,线性回归 f ( x ) = w T x + b f(\bm{x}) = \bm{w}^T\bm{x} + b f(x)=wTx+b的值域是 ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞),而我们所求概率的值域一定是限制在 [ 0 , 1 ] [0,1] [0,1]之间,所以线性回归是不符合要求的,于是,我们可以引入这样一个函数:Sigmoid函数,也被称作逻辑函数(Logistic function)。
Sigmoid函数的表达式和函数图像
σ ( x ) = 1 1 + e − x \sigma(x) =\frac{1}{1+e^{-x}} σ(x)=1+e−x1
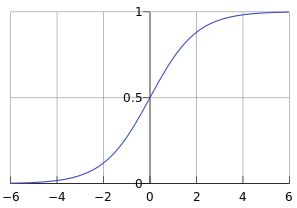
由函数图像即可看出,Sigmoid函数的值域在01之间,在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要。
实际上,我们把Sigmoid函数作为对线性回归模型的处理函数来使用,也就是说我们把 z = w T x + b \bm{z}= \bm{w}^T\bm{x} + b z=wTx+b的输出z值作为Sigmoid函数的自变量。
所以,我们需要的逻辑回归模型的表达式如下:
y = σ ( f ( x ) ) = σ ( w T x ) = 1 1 + e − w T x y=\sigma(f(\bm{x})) = \sigma(\bm{w}^T\bm{x})=\frac{1}{1+e^{-\bm{w}^T\bm{x}}} y=σ(f(x))=σ(wTx)=1+e−wTx1
这个函数的意思就是在给定 x 和 w w w的条件下 y=1 的概率。
与之相对应的决策函数为:
y^ = 1, if P(y=1|x)>0.5
选择0.5作为阈值是一个一般的做法,实际应用时特定的情况可以选择不同阈值,如果对正例的判别准确性要求高,可以选择阈值大一些,对正例的召回要求高,则可以选择阈值小一些。
逻辑回归的损失函数(Cost Function)
简单来说,损失函数反映的是通过逻辑回归得到的结果与真实值的差异大小,一般来说,Cost越小,说明损失越小,损失函数越小说明模型和参数越符合训练样本。
对于损失函数的推导这里不做赘述。

其中, p = 1 1 + e − w T x p = \frac{1}{1+e^{-\bm{w}^T\bm{x}}} p=1+e−wTx1
这个函数 F ( w ) F(\bm{w}) F(w) 又叫做它的损失函数。损失函数可以理解成衡量我们当前的模型的输出结果,跟实际的输出结果之间的差距的一种函数。
梯度下降法
既然上文说过了,损失函数的值越小,说明我们的分类值和实际上的值的差距越小,所以我们就要想方设法把损失函数最小化,而梯度下降法就是这个作用。
梯度下降法(英语:Gradient descent是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
就好似下山,我们在每一个点都向下山最快的方向走,无疑能达到山的最底部。
具体操作,就是对b和w不断迭代求偏导,找到能得到Cost函数最小值取值时的值由于逻辑回归时b的取值可为0,此处不考虑。
w t + 1 = w t − η ∗ d w \bm{w}_{t+1} = \bm{w}_t-\eta*dw wt+1=wt−η∗dw
这里的 η \eta η是另一个可以设置的参数,叫做学习率。迭代次数也是有人为控制。
至此,逻辑回归的简单介绍到此结束,有些数学推导未能列出来,请读者自行查阅