强化学习笔记+代码（四）：DQN算法原理和Agent实现

本文主要整理和参考了李宏毅的强化学习系列课程和莫烦python的强化学习教程
本系列主要分几个部分进行介绍

1. 强化学习背景介绍
2. SARSA算法原理和Agent实现
3. Q-learning算法原理和Agent实现
4. DQN算法原理和Agent实现(tensorflow)
5. Double-DQN、Dueling DQN算法原理和Agent实现(tensorflow)
6. Policy Gradients算法原理和Agent实现(tensorflow)
7. Actor-Critic、A2C、A3C算法原理和Agent实现(tensorflow)

一、DQN算法原理

DQN其实就是Q-learning的一种实现框架，在最早的Q-learning重，是通过Q-table来找到$Q(s,a)$，这是查找是一种映射关系。但是当状态很多或者动作连续时Q-table变得很难处理，既然是映射关系就可以使用神经网络。
先回顾一下前面的知识
化学习的主要功能就是让agent学习尽可能好的动作action，使其后续获得的奖励尽可能的大。
假设在时刻t时，长期（全局）奖励为：

其中$r_{t+n}$为t+n时获得的局部奖励，$\gamma$为下一期奖励传递到当期的衰减因子。则状态s的价值为$G_t$的条件期望：

同样定义状态s时执行动作a的价值也为$G_t$的条件期望：

可知：$E(Q_{\pi }(s,a))=V_{\pi }(s)$
下面直接给出深度学习最核心的Bellman 公式

Bellman 公式十分的直观，$V_{\pi }(s)$=根据动作走到下个状态的奖励+下个状态长期价值*衰减值的期望。价值会不断的传递，因此可以看出$V_{\pi }(s)$衡量的是状态s的长期价值。
因为RL需要是Agent不断变强，就可以理解为让状态或让动作的价值不断变大，因此会选择根据如下方式获得新的$V_{\pi }(s)$和$Q_{\pi }(s,a)$

下面先给出DQN算法：

上面算法中核心思想与Q-learning一样：求出$Q_{\ast }(s,a)=r+\gamma max[Q(s^{\prime },a^{\prime })]$是关键。
具体的，我们可以学习某个状态s的评价$V_{\pi }(s)$，也可以学习某个状态s休执行动作a的评价$Q(s,a)$。

1. 学习$V_{\pi }()$

当学习某个状态s的评价$V_{\pi }(s)$时$V_{\pi }()$就我们要学习的函数，可用如下结构表示：

其中$V_{\pi }(s)$的获得有如下两种方式：
1. Monte-Carlo (MC) based approach ：

我们再状态$s_a$下执行一些列动作，直到游戏结束，和观测到这一系列奖励的总和$G_a$，我们直接将$G_a$赋值给$V_{\pi }(s)$，即用如下公式更新：

2.Temporal-difference (TD) approach ：

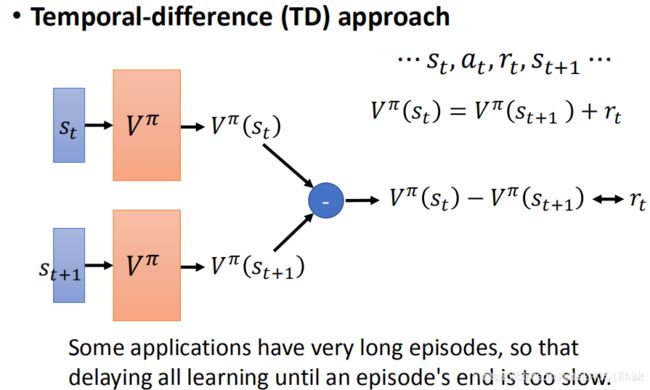
在一种方法MC中，我们必须达到游戏结束状态才能计算出$s_t$的价值。但是由于传递性，我们可以通过$s_{t+1}$的价值与状态$s_t$的奖励$=r_t$的组合来求解$s_t$的价值。具体的更新公式为：

实际上，MC由于要进行一系列动作，链条较长，不稳定，因此方差较大，但可以看做全局的方式，精度较高；而TD的方式由于误差不断传递，导致精度稍低，但是只有$=r_t$存在方差，因此方差比较小

2. 学习$Q_{\pi }()$
   上面是学习状态的价值$V_{\pi }(s)$，实际上更常用的方式是求解状态s下动作a的价值$Q_{\pi }(s,a)$，对于此DQN结构，有两种构建方式，一种是输入状态s，输出该状态下没每一种动作的价值。一种是输入状态s和动作a，输出状态s下执行动作a的价值：
   
   
   神经网络输出的价值$Q(s,a)$，假设我们再状态s下有一个动作：(s,a)，执行完到达状态s’,继续执行a’达到(s’,a’)。通过神经网络可以求出$Q(s,a)$和$Q(s^{\prime },a^{\prime })$，其中$Q_{\ast }(s,a)=r+\gamma max[Q(s^{\prime },a^{\prime })]$，则可根据$Q_{\ast }(s,a)与Q(s,a)$的差距来对$Q$进行学习。这与Q-learning的思路是一致的。

但上面算法中，也有一些与与Q-learning不同的地方，这是使DQN变得更加有效和技巧：

1. target network
   目标是学习网络$Q$，我们记录为eval network。根据公式，更新时需要求解$Q_{\ast }(s,a)=r+\gamma max[Q(s^{\prime },a^{\prime })]$，这里的$Q(s^{\prime },a^{\prime })=Q^{\pi }(s_{t+1},\pi (s_{t+1}))$，是网络在$S_{t+1}$的输出，由于网络的eval network一直在更新，导致$Q_{\ast }(s,a)$和$Q(s,a)$一直在变化的，是会是训练十分不稳定。
   解决办法是我们使用一个与eval network结构相同的target network来计算$Q_{\ast }(s,a)$。其中target network使用的eval network较老的参数，eval network每训练n次才更新一次target network（方式是直接将eval network的参数赋值给target network）。这样在一定时间内就相当于固定了$Q_{\ast }(s,a)$，使得训练变得稳定。
   
2. replay buffer
   把之前与环境互动的记录 (st,at,rt,st+1)放到一个buffer里面，随机抽取buffer中的n条记录来训练神经网络。
   其中buffer里面的记录可能来自采取不同时期的神经网络。比如互动产生10000个(st,at,rt,st+1)后就更新一次网络参数，buffer的储存上限为50000个(st,at,rt,st+1)，这使得buffer中可能储存着之前5次更新神经网络的产生的记录。
   这样做的好处是buffer中的记录可以反复被使用，减少了交互所浪费的时间。同时增加数据多样性，降低batch内相关性，提高泛化性能，训练效果更好。
   

三、DQN Agent代码

此处直接参考莫烦python的强化学习教程进行代码编写，在基础上说明每一行代码的用途
采用此种神经网络结构：

import numpy as np
import pandas as pd
import tensorflow as tf
from maze_env_drl import Maze    #即为environment

class DeepQNetwork(object):
    #replace_target_iter为更新target network的步数，防止target network和eval network差别过大
    #memory_size为buffer储存记忆上线，方便使用以前记忆学习
    def __init__(self, n_actions, n_features,learning_rate=0.01,reward_decay=0.9,e_greedy=0.9,replace_target_iter=300,memory_size=500,batch_size=32,e_greedy_increment=None,output_graph=False):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate
        self.gamma = reward_decay
        self.epsilon_max = e_greedy     # epsilon后面奖励对前面的递减参数
        self.replace_target_iter = replace_target_iter  # 更换 target_net 的步数
        self.memory_size = memory_size  # 记忆上限
        self.batch_size = batch_size    # 每次更新时从 memory 里面取多少记忆出来
        self.epsilon_increment = e_greedy_increment # epsilon 的增量
        #epsilon = 0等于0时，后面的奖励创传不到前面，前面的状态就开启随机探索模式
        self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max # 是否开启探索模式, 并逐步减少探索次数
        
        # 记录学习次数 (用于判断是否更换 target_net 参数)
        self.learn_step_counter = 0
        
        # 初始化全 0 记忆 [s, a, r, s_]， 实际上feature为状态的维度，n_features*2分别记录s和s_，+2记录a和r
        self.memory = np.zeros((self.memory_size, n_features*2+2))
        #构建网络
        self._build_net()
        
        #替换 target net 的参数
        t_params = tf.get_collection('target_net_params')  #提取 target_net 的参数
        e_params = tf.get_collection('eval_net_params')   # 提取  eval_net 的参数
        #将eval_network中每一个variable的值赋值给target network的对应变量
        self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)] #更新 target_net 参数
        
        
        self.sess = tf.Session()
        
        if output_graph:
            tf.summary.FileWriter("logs/", self.sess.graph)
        
        self.sess.run(tf.global_variables_initializer())
        #用于记录# 记录所有 cost 变化
        self.cost_his = []
    
    #李宏毅老师克重的relpay buffer，通过以往的记忆中不断训练
    #这是DQN变为off-policy的核心
    def store_transition(self, s, a, r, s_):
        #如果DeepQNetwork中定义了memory_counter，进行记忆存储
        if not hasattr(self, 'memory_counter'):
            self.memory_counter = 0
        
        #记录一条 [s, a, r, s_] 记录
        transition = np.hstack((s, [a, r], s_))
        
        #总 memory 大小是固定的, 如果超出总大小, 旧 memory 就被新 memory 替换
        index = self.memory_counter % self.memory_size  #类似hashmap赋值思想
        self.memory[index, :] = transition  #进行替换
        
        self.memory_counter += 1
        
    #建立神经网络
    #此处建立两个申请网络，一个为target network，用于得到q现实。一个为eval_network，用于得到q估计
    #target network和eval_network结构一样，target network用比较老的参数，eval_network为真正训练的神经网络
    def _build_net(self):
        tf.reset_default_graph()  #清空计算图
        
        #创建eval神经网络,及时提升参数
        self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s')  # 用来接收 observation，即神经网络的输入
        self.q_target = tf.placeholder(tf.float32, [None, self.n_actions], name='Q_target') # q_target的值, 这个之后会通过计算得到，神经网络的输出
        #eval_net域下的变量
        with tf.variable_scope('eval_net'):
            #c_names用于在一定步数之后更新target network
            #GLOBAL_VARIABLES作用是collection默认加入所有的Variable对象，用于共享
            c_names = ['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
            n_l1 = 10  #n_l1为network隐藏层神经元的个数 
            w_initializer = tf.random_normal_initializer(0.,0.3)  
            b_initializer = tf.constant_initializer(0.1)
            
            #eval_network第一层全连接神经网络
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s, w1)+b1)
            
            #eval_network第二层全连接神经网络
            with tf.variable_scope('l1'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                #求出q估计值，长度为n_actions的向量
                self.q_eval = tf.matmul(l1, w2) + b2
            
        with tf.variable_scope('loss'): # 求误差
            #使用平方误差
            self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
        
        with tf.variable_scope('train'):    # 梯度下降
            optimizer = tf.train.RMSPropOptimizer(self.lr)
            self._train_op = optimizer.minimize(self.loss)
        
        #创建target network，输入选择一个action后的状态s_,输出q_target
        self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')    # 接收下个 observation
        with tf.variable_scope('target_net'):
            c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
            
            # target_net 的第一层fc， collections 是在更新 target_net 参数时会用到
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)
                
            # target_net 的第二层fc
            with tf.variable_scope('l2'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                #申请网络输出
                self.q_next = tf.matmul(l1, w2) + b2
                
    def choose_action(self, observation):
        #根据observation（state）选行为
        #使用eval network选出state下的行为估计
        #将observation的shape变为(1, size_of_observation)，行向量变为列向量才能与NN维度统一
        observation = observation[np.newaxis, :]
        
        if np.random.uniform() < self.epsilon:
            action_value = self.sess.run(self.q_eval, feed_dict={self.s:observation})
            action = np.argmax(action_value)
            
        else:
            action = np.random.randint(0, self.n_actions)   #随机选择
        
        return action
    
    def learn(self):
        if self.learn_step_counter % self.replace_target_iter ==0:
            self.sess.run(self.replace_target_op)
            print('\ntarget_params_replaced\n')
        
        #从memory中随机抽取batch_size这么多记忆
        if self.memory_counter > self.memory_size:   #说明记忆库已经存满，可以从记忆库任意位置收取
            sample_index = np.random.choice(self.memory_size, size=self.batch_size)
        else:   #记忆库还没有存满，从现有的存储记忆提取
            sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
        
        batch_memory= self.memory[sample_index, :]
        
        # 获取q_next即q现实(target_net产生的q)和q_eval(eval_net产生的q)
        #q_next和q_eval都是一个向量，包含了对应状态下所有动作的q值
        #实际上feature为状态的维度，batch_memory[:, -self.n_features:]为s_,即状态s采取动作action后的状态s_, batch_memory[:, :self.n_features]为s
        q_next, q_eval = self.sess.run([self.q_next, self.q_eval], feed_dict={self.s_: batch_memory[:, -self.n_features:],self.s: batch_memory[:, :self.n_features]})
        
        #下面这几步十分重要. q_next, q_eval 包含所有 action 的值, 而我们需要的只是已经选择好的 action 的值, 其他的并不需要.所以我们将其他的 action 值全变成 0, 将用到的 action 误差值 反向传递回去, 作为更新凭据.
        #这是我们最终要达到的样子, 比如 q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
        # q_eval = [-1, 0, 0] 表示这一个记忆中有我选用过 action 0, 而action0带来的 Q(s, a0)=-1,而其他的 Q(s, a1)=Q(s, a2)=0
        # q_target = [1, 0, 0] 表示这个记忆中的 r+gamma*maxQ(s_) = 1, 而且不管在 s_ 上我们取了哪个 action
        # 我们都需要对应上 q_eval 中的 action 位置, 所以就将 q_target的1放在了 action0的位置.
        
        # 下面也是为了达到上面说的目的, 不过为了更方面让程序运算, 达到目的的过程有点不同.# 是将 q_eval 全部赋值给 q_target, 这时 q_target-q_eval 全为 0,
        # 不过 我们再根据 batch_memory 当中的 action 这个 column 来给 q_target 中的对应的 memory-action 位置来修改赋值.
        # 使新的赋值为 reward + gamma * maxQ(s_), 这样 q_target-q_eval 就可以变成我们所需的样子.
        
        q_target = q_eval.copy()
        #每个样本下标
        batch_index = np.arange(self.batch_size, dtype=np.int32)
        #记录每个样本在st时刻执行的动作
        eval_act_index = batch_memory[:, self.n_features].astype(int)
        #记录每个样本动作的奖励
        reward = batch_memory[:, self.n_features + 1]
        
        #生成每个样本中q值对应动作的更新，即生成的q现实，
        q_target[batch_index, eval_act_index]=reward+self.gamma * np.max(q_next, axis=1)
                
        #假如在这个 batch 中, 我们有2个提取的记忆, 根据每个记忆可以生产3个 action 的值:
        #q_eval =[[1, 2, 3],[4, 5, 6]]， 另q_target = q_eval.copy()
        
        #然后根据memory当中的具体action位置来修改 q_target 对应 action 上的值:
        #比如在:记忆 0的q_target计算值是 -1,而且我用了action0;忆1的q_targe 计算值是-2, 而且我用了action2:
        #q_target =[[-1, 2, 3],[4, 5, -2]]
        #所以 (q_target - q_eval) 就变成了:[[(-1)-(1), 0, 0],[0, 0, (-2)-(6)]]
        #最后我们将这个 (q_target - q_eval) 当成误差, 反向传递会神经网络
        #所有为 0 的 action 值是当时没有选择的 action, 之前有选择的 action 才有不为0的值.
        #我们只反向传递之前选择的 action 的值,
        _, self.cost = self.sess.run([self._train_op, self.loss],feed_dict={self.s: batch_memory[:, :self.n_features],self.q_target: q_target})
        
        self.cost_his.append(self.cost) # 记录 cost 误差
        
        #每调用一次learn，降低一次epsilon，即行为随机性
        self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
        
        self.learn_step_counter += 1
        
    def plot_cost(self):
        import matplotlib.pyplot as plt
        plt.plot(np.arange(len(self.cost_his)), self.cost_his)
        plt.ylabel('Cost')
        plt.xlabel('training steps')
        plt.show()

def run_maze():
    step = 0
    for episode in range(300):
        # 初始化环境
        observation = env.reset()
        
        while True:
            # 刷新环境
            env.render()
            
            # DQN 根据观测值选择行为
            action = RL.choose_action(observation)   #一种off-poliy的方法
            
            # 环境根据行为给出下一个 state, reward, 是否终止
            observation_, reward, done = env.step(action)
            
            # DQN 存储记忆
            #即存在李宏毅老师课中的replay buffer，便于使用以前的记忆训练
            RL.store_transition(observation, action, reward, observation_)   
            
            # 控制学习起始时间和频率 (先累积一些记忆再开始学习)
            if (step>200) and (step % 5 == 0):
                RL.learn()
            
            # 将下一个 state_ 变为 下次循环的 state
            observation = observation_
            
            # 如果终止, 就跳出循环
            if done:
                break
            
            step+=1
    
    print('game over')
    env.destroy()
    
if __name__=="__main__":
    env = Maze()
    #replace_target_iter为更新target network的步数，即莫烦中的fixed Q-targets
    #memory_size为replay buffer的储存上限，用于不在实际交互下也能进行训练，即莫烦中的memory
    RL = DeepQNetwork(env.n_actions,env.n_features,learning_rate=0.01,reward_decay=0.9,e_greedy=0.9,replace_target_iter=200,memory_size=2000,output_graph=True)
    
    env.after(100, run_maze)
    env.mainloop()
    RL.plot_cost()