DBSCAN算法学习笔记及scala实现

一、算法概述

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法，相比其他的聚类方法，基于密度的聚类方法可以在有噪音的数据中发现各种形状和各种大小的簇。基于密度的聚类是寻找被低密度区域分离的高密度区域，这些高密度区域就是一个一个的簇，这里的密度指的是一个样本点的领域半径内包含的点的数目，基于密度的聚类方法可以用来过滤噪声孤立点数据，发现任意形状的簇（因为它将簇定义为密度相连的点的最大集合），与k-means算法的不同之处在于它不需要事先指定划分的簇的数目。

二、算法涉及的基本概念

（1）$\epsilon$领域：给定对象半径$\epsilon$内的区域，半径的大小由参数Eps表示。
（2）核心点：如果给定对象$ϵ$领域内的样本点数大于等于MinPts，则称该对象为核心对象，其中MinPts是用户指定的参数。
　　

（3）边界点：如果一个对象是非核心对象，但它的领域中有核心对象，则为边界点。
（4）噪声点：除核心对象和边界对象之外的点。
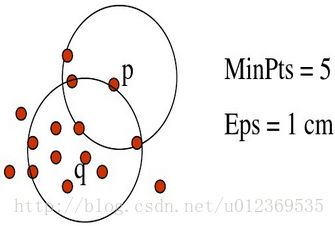
（5）直接密度可达：给定一个对象集合D，如果p在q的$\epsilon$领域内，且q是一个核心对象，则我们说对象p从对象q出发是直接密度可达的。
（6）密度可达：对于样本集合D，如果存在一个对象链$p_1$,$p_2$,…,$p_n$，$p_1$ = 1,$p_n$ = p，对于$p_i$ $ϵ$ D,$p_i+1$是从$p_i$关于$\epsilon$和MinPts直接密度可达，则对象p是从对象q关于$\epsilon$和MinPts密度可达。
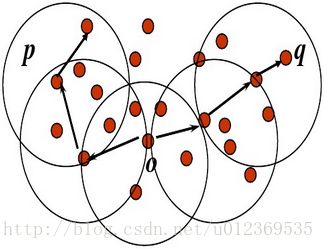
（7）密度相连：如果存在对象o$ϵ$D，使对象p和q都是从o关于$\epsilon$和MinPts密度可达的，那么对象p到q是关于$\epsilon$和MinPts密度相连的。
　　

可以发现，密度可达是直接密度可达的传递闭包，并且这种关系是非对称的，因为q不一定是核心对象，如果q为边界点，则q到p一定不密度可达。只有核心对象之间相互密度可达，然而密度相连是对称关系。

三、算法步骤

1.标记所有对象为unvisited
2.Do
3.随机选择一个unvisited对象p
4.标记p为visited
5.If p的$ϵ$领域至少有MinPts个对象
6. 　创建一个新簇Ｃ，并把ｐ添加到Ｃ中
7.　 令Ｎ为ｐ的$ϵ$领域中的对象集合
8. For N中每个点p${}^{\prime }$
9. 　　if p${}^{\prime }$是unvisited　
10.　　　标记p${}^{\prime }$为visited，将p${}^{\prime }$添加到C
11.　　　if p${}^{\prime }$的$\epsilon$领域至少有MinPts个对象，把这些对象中未分类的对象划分到C中，并把这些对象全都添加到N中
12.　　　end if　
13.　 end if
14.　　将p${}^{\prime }$从N中剔除
15.　End for（直到N为空集）
16.Else 标记p为噪声点
17.Until没有标记为unvisite的对象（直到所有对象被访问）
　　
DBSCAN目的是找到密度相连对象的最大集合。我的理解是每次聚类都是寻找到某一个核心点，然后基于该核心点的领域半径内的点集A出发，寻找下一个核心点，其领域半径内的点集B合并到A里，再次从扩大的集合A里寻找新的核心点，直到这个集合A不再扩大为止，此时集合A即为密度相连点的最大集合，这个集合里的各点之间的密度相连都是对于第一次寻找到的核心点来说的。
　　　

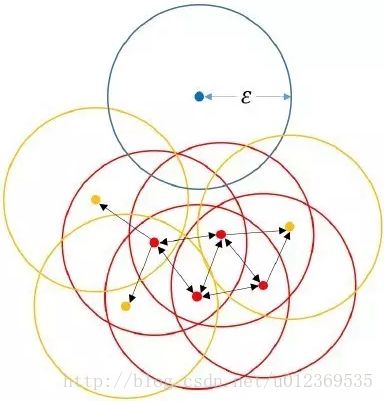
当设置MinPts=4的时候，红点为高密度点，蓝点为异常点，黄点为边界点。红黄点串成一起成了一个簇。
　
“其核心思想就是先发现密度较高的点，然后把相近的高密度点逐步都连成一片，进而生成各种簇。算法实现上就是，对每个数据点为圆心，以eps为半径画个圈（称为邻域eps-neigbourhood），然后数有多少个点在这个圈内，这个数就是该点密度值。然后我们可以选取一个密度阈值MinPts，如圈内点数小于MinPts的圆心点为低密度的点，而大于或等于MinPts的圆心点高密度的点（称为核心点Core point）。如果有一个高密度的点在另一个高密度的点的圈内，我们就把这两个点连接起来，这样我们可以把好多点不断地串联出来。之后，如果有低密度的点也在高密度的点的圈内，把它也连到最近的高密度点上，称之为边界点。这样所有能连到一起的点就成一了个簇，而不在任何高密度点的圈内的低密度点就是异常点。”

四、代码实现

package DBSCAN
import scala.collection.mutable.ArrayBuffer
import scala.io.Source
import scala.util.control.Breaks._
object myDBSCAN {

  def main(args: Array[String]): Unit = {
    val minPts = 5 //密度阈值
    val ePs = 1.39 //领域半径
    val dim = 2 //数据集维度
    //处理输入数据
    val fileName = "D:\\dbscan_data.txt"
    val lines = Source.fromFile(fileName).getLines()
    val points = lines.map(line => {//数据预处理
    val parts = line.split("\t").map(_.toDouble)
      var vector = Vector[Double]()
      for(i <- 0 to dim - 1)
        vector ++= Vector(parts(i))
      vector
    }).toArray
    println("数据集点的x坐标如下：")
    points.foreach(v => print(v(0)+","))
    println()
    println("数据集点的y坐标如下：")
    points.foreach(v => print(v(1)+","))
    println()
    val (cluster,types) = runDBSCAN(points,ePs,minPts)
    printResult(points,cluster,types)

  }

  def runDBSCAN(data:Array[Vector[Double]],ePs:Double,minPts:Int):(Array[Int],Array[Int]) ={
      val types = (for(i <- 0 to data.length - 1) yield -1).toArray //用于区分核心点1，边界点0，和噪音点-1(即cluster中值为0的点)
      val visited = (for(i <- 0 to data.length - 1) yield 0).toArray //用于判断该点是否处理过，0表示未处理过
      var number = 1 //用于标记类
      var xTempPoint = Vector(0.0,0.0)
      var yTempPoint = Vector(0.0,0.0)
      var distance = new Array[(Double,Int)](1)
      var distanceTemp = new Array[(Double,Int)](1)
      val neighPoints = new ArrayBuffer[Vector[Double]]()
      var neighPointsTemp = new Array[Vector[Double]](1)
      val cluster = new Array[Int](data.length) //用于标记每个数据点所属的类别
      var index = 0
      for(i <- 0 to data.length - 1){//对每一个点进行处理
         if(visited(i) == 0){ //表示该点未被处理
           visited(i) == 1 //标记为处理过
           xTempPoint = data(i) //取到该点
           distance = data.map(x => (vectorDis(x,xTempPoint),data.indexOf(x)))//取得该点到其他所有点的距离Array{(distance,index)}
           neighPoints ++= distance.filter(x => x._1 <= ePs).map(v => data(v._2)) //找到半径ePs内的所有点(密度相连点集合)

           if(neighPoints.length > 1 && neighPoints.length < minPts){
             breakable{
               for(i <- 0 to neighPoints.length -1 ){//此为非核心点，若其领域内有核心点，则该点为边界点-------------------------------new------------------------
                 var index = data.indexOf(neighPoints(i))
                 if(types(index) == 1){
                   types(i) = 0//边界点--------------------------------new---------------------------
                   break
                 }
               }
             }
           }
           if(neighPoints.length >= minPts){//核心点,此时neighPoints表示以该核心点出发的密度相连点的集合
             types(i) = 1
             cluster(i) = number
             while(neighPoints.isEmpty == false){ //对该核心点领域内的点迭代寻找核心点，直到所有核心点领域半径内的点组成的集合不再扩大（每次聚类 ）
               yTempPoint =neighPoints.head //取集合中第一个点
               index = data.indexOf(yTempPoint)
               if(visited(index) == 0){//若该点未被处理，则标记已处理
                 visited(index) = 1
                 if(cluster(index)==0) cluster(index) = number //划分到与核心点一样的簇中
                 distanceTemp = data.map(x => (vectorDis(x,yTempPoint),data.indexOf(x)))//取得该点到其他所有点的距离Array{(distance,index)}
                 neighPointsTemp = distanceTemp.filter(x => x._1 <= ePs).map(v => data(v._2)) //找到半径ePs内的所有点

                 if(neighPointsTemp.length >= minPts) {
                   types(index) = 1 //该点为核心点
                   for (i <- 0 to neighPointsTemp.length - 1) {
                     //将其领域内未分类的对象划分到簇中,然后放入neighPoints
                     if (cluster(data.indexOf(neighPointsTemp(i))) == 0) {
                       cluster(data.indexOf(neighPointsTemp(i))) = number //只划分簇，没有访问到
                       neighPoints += neighPointsTemp(i)
                     }
                   }
                 }
                 if(neighPointsTemp.length > 1 && neighPointsTemp.length < minPts){//------------new---------------
                   breakable{
                     for(i <- 0 to neighPointsTemp.length -1 ){//此为非核心点，若其领域内有核心点，则该点为边界点
                       var index1 = data.indexOf(neighPointsTemp(i))
                       if(types(index1) == 1){
                         types(index) = 0//边界点--------------------------------new---------------------------
                         break
                       }
                     }
                   }
                 }
               }
               neighPoints-=yTempPoint //将该点剔除
             }//end-while
             number += 1 //进行新的聚类
           }
         }
      }
    (cluster,types)
  }

  def printResult(data:Array[Vector[Double]],cluster:Array[Int],types:Array[Int]) = {
    val result = data.map(v => (cluster(data.indexOf(v)),v)).groupBy(v => v._1) //Map[int,Array[(int,Vector[Double])]]
    //key代表簇号，value代表属于这一簇的元素数组
    result.foreach(v =>{
      println("簇" + v._1 + "包含的元素如下:")
      v._2.foreach(v => println(v._2))
    })
    //val noise = cluster.zip(data).filter(v => v._1 ==0)
    //noise.foreach(v => types(data.indexOf(v._2)) = -1) //通过簇号0把噪音点在types中赋值-1,数据集中没有包含在任何簇中(即簇号为0)的数据点就构成异常点
    val pointsTypes = data.map(v => (types(data.indexOf(v)),v)).groupBy(v => v._1) //Map[点类型int,Array[(点类型int,Vector[Double])]]
    //key代表点的类型号，value代表属于这一类型的元素数组
    pointsTypes.foreach(v =>{
      if(v._1 == 1) println("核心点如下：")
      else if(v._1 ==0) println("边界点如下：")
      else println("噪音点如下：")
      v._2.foreach(v => println(v._2))
    })
    val resultMat = cluster.zip(types).zip(data) //Array[((Int,Int),Vector[Double])],即Array[((簇Id，类型Id),点向量)]
    val resultMat1 = resultMat.groupBy(v => v._1) //Map[(Int,Int),Array[((Int,Int),Vector[Double])]]
    resultMat1.foreach(v => {
      val arr = v._2
      if(v._1._2 == 1){
        println("簇"+v._1._1+"的核心点集的x坐标为：")
        arr.foreach(v => print(v._2(0)+","))
        println()
        println("簇"+v._1._1+"的核心点集的y坐标为：")
        arr.foreach(v => print(v._2(1)+","))
        println()
      }else if(v._1._2 == 0){
        println("簇"+v._1._1+"的边界点集的x坐标为：")
        arr.foreach(v => print(v._2(0)+","))
        println()
        println("簇"+v._1._1+"的边界点集的y坐标为：")
        arr.foreach(v => print(v._2(1)+","))
        println()
      }else{
        println("噪音点集的x坐标为：")
        arr.foreach(v => print(v._2(0)+","))
        println()
        println("噪音点集的y坐标为：")
        arr.foreach(v => print(v._2(1)+","))
        println()
      }
    })
  }
  //--------------------------自定义向量间的运算-----------------------------
  //--------------------------向量间的欧式距离-----------------------------
  def vectorDis(v1: Vector[Double], v2: Vector[Double]):Double = {
    var distance = 0.0
    for(i <- 0 to v1.length - 1){
      distance += (v1(i) - v2(i)) * (v1(i) - v2(i))
    }
    distance = math.sqrt(distance)
    distance
  }
}

其中我对于数据集数组points，另生成types、visited和cluster数组，分别对应数据点的类型、是否访问以及所属的簇号，对于噪音点的判断，是结合types和cluster数组，types中值为1表示核心点，0表示边界点（默认初始化）或噪音点，cluster数组中值大于等于1的表示簇号，值为0表示不属于任一簇（即噪音点），在cluster中找到值为0的数据对应的索引号，根据索引号在types中将相应数据值赋为-1（噪音点），则types数组即可表示所有数据点的类型。
　　
原始数据集图像如下：
　　

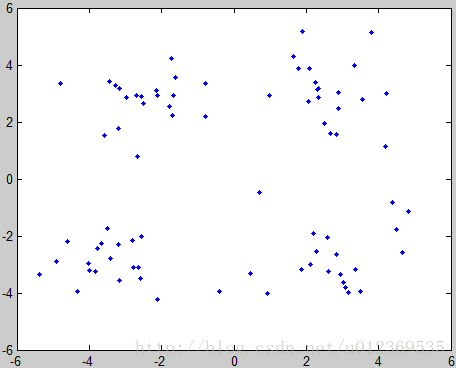
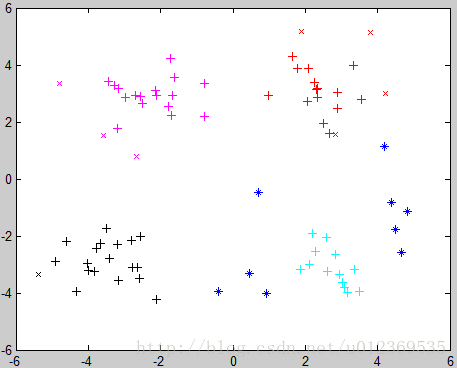
　　执行DBSCAN聚类后的图像如下：
　　

其中，蓝色表示噪音点，其他四种颜色表示四类簇，+表示核心点，×表示边界点，但是感觉最下面的三个噪音点看起来很别扭的样子，而且右下方的簇竟然没有边界点，可能代码还是不完善o(╥﹏╥)o

参考文献

[1]http://blog.csdn.net/google19890102/article/details/37656733
[2]http://blog.csdn.net/wu5151/article/details/50622397
[3]http://www.52ml.net/10326.html　
[4]http://mp.weixin.qq.com/s/ORLOOhufrInyPdS6fbywOw