卷积神经网络的基本概念与mnist测试

CNN

简介

• 视觉皮质有一块很小的局部感受野(local receptive feld)。不同的感受野之间可能会发生重叠，所有的感受野组成了可视区域
• 对视觉皮质的研究最终演化为CNN，CNN除了之前的全连接层以及激活函数等概念，还引入了卷积层和池化层等概念

setup code

# 不显示python使用过程中的警告
import warnings
warnings.filterwarnings("ignore")

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import os

# 这个options只需要在之后第一次使用Session时使用就可以了
gpu_options = tf.GPUOptions(allow_growth=True)

def reset_graph(seed=42):
    tf.reset_default_graph()
    tf.set_random_seed(seed)
    np.random.seed(seed)
    return

# with tf.Session( config=tf.ConfigProto(gpu_options=gpu_options) ) as sess:
with tf.Session(  ) as sess:
    print( sess.run( tf.constant(1) ) )

1

卷积层

• 之前的dnn中，每一个网络层的所有节点都与之前的所有节点相连；而在CNN中，第一个卷积层中的神经元并非与输入图像中的所有节点都连接，它们只与感受野内的像素有关。同时第二层卷积层也只与第一层卷积层的部分节点连接。
• 这种结构使得网络可以在第一层隐含层内提取低阶特征，然后在下一层隐含层中再集成为高阶特征，这与真实情况很符合，其效果也十分显著。
• 在之前训练多层神经网络中，每一层的网络中的每一个样本都是1D的向量，在CNN中，每一层中的每个样本可以表示为2D的矩阵（图像）。
• 对于一个特定的网络层，它在 (i,j) ( i , j ) 处的神经元与前一层中 [i,i+fh−1,j,j+fw−1] [ i , i + f h − 1 , j , j + f w − 1 ] (行的下限与上限、列的下限与上限)区域的神经元相连接。因此如果不做额外的处理，两个网络层的尺寸往往不同；一般会再前一层的边缘补充0元素，这就是zero padding。
• 如果调整感受野之间的间距（上一步中说的间距为1），可以进一步减小下一网络层的大小。 (i,j) ( i , j ) 位置处的神经元与前一层中的 [i×sh,i×sh+fh−1,j×sw,j×sw+fw−1] [ i × s h , i × s h + f h − 1 , j × s w , j × s w + f w − 1 ] 。其中 sh s h 与 sw s w 是竖直与水平方向的步长。

filters

• 一个神经元节点的权重的大小就是其感受野的大小，这个权重矩阵就是卷积核(convolution kernels)
• 不同的神经元之间的卷积核如果相同，则可以实现权重共享，大大减少CNN的参数量

feature map

• 之前提到的是只对一幅图像提取一种特征，但是如果有很多个特征，则可以建立卷积层的feature map，每个feature map实现权值共享，但是不同的卷积层之间的参数可能不同。即，一个卷积层同时用多个卷积核对它的输入做处理，以便于检测输入的多种特征。
• 输入图像也可以不仅仅是2D图像，也可以包含3维信息（RGB）
• 一个CNN上(i,j,k)处的值为
  
  zi,j,k=bk+∑i′=i×shi×sh+fh−1∑j′=j×swj×sw+fw−1∑k′=1fn′xx′,j′,k′wx′,j′,k′,k z i , j , k = b k + ∑ i ′ = i × s h i × s h + f h − 1 ∑ j ′ = j × s w j × s w + f w − 1 ∑ k ′ = 1 f n ′ x x ′ , j ′ , k ′ w x ′ , j ′ , k ′ , k
  
  其中 xi′,j′,k′ x i ′ , j ′ , k ′ 是前一层神经元在第 k′ k ′ 层feature map上的输出， bk b k 是偏置项，w是权值矩阵，因此每一层的权重参数维度为 fh×fw×fk′×fk f h × f w × f k ′ × f k

TF中卷积层的使用

• TF中输入图像可以被表示为3D的tensor， [height,width,channels] [ h e i g h t , w i d t h , c h a n n e l s ] ，一个batch是4D的tensor， [batch_size,height,width,channels] [ b a t c h _ s i z e , h e i g h t , w i d t h , c h a n n e l s ] ，卷积核的权重是一个4D的tensor， [fh,fw,fn,fn′] [ f h , f w , f n , f n ′ ] （ fn f n , fn′ f n ′ 分别是当前和上一层网络的feature map个数），偏置为1D的tensor， [fn] [ f n ] ，即当前神经网络中，每一个feature map的偏置都不一样。
• strides参数是一个有1X4的向量，其中strides[0]=strides[3]=1，另外2个数分别是在行和列上的步长
• padding为”SAME”时，会在边缘补0，为VALID时，得到的图像大小会比之前的小

from sklearn.datasets import load_sample_images

dataset = np.array( load_sample_images().images, dtype=np.float32 )
batch_size, height, width, channels = dataset.shape
print( dataset.shape )

# 卷积核，包含水平和竖直2个方向的特征
filters = np.zeros( shape=(7,7,channels,3), dtype=np.float32 )
filters[:,3,:,0] = 1
filters[3,:,:,1] = 1

# 与dataset的尺寸相同，相当于将dataset作为输入
X = tf.placeholder( tf.float32, shape=(None, height, width, channels) )
convolution = tf.nn.conv2d( X, filters, strides=[1,2,2,1], padding="SAME" )

with tf.Session() as sess:
    output = sess.run( convolution, feed_dict={X:dataset} )
print( output.shape )
plt.figure( figsize=(10,5) )
plt.subplot(121)
plt.imshow( output[1,:,:,0] )
plt.subplot(122)
plt.imshow( output[1,:,:,1] )
plt.show()

(2, 427, 640, 3)
(2, 214, 320, 3)

• CNN中有一些超参数需要调节，比如卷积核个数、大小、步长、padding方式等，可以通过交叉验证的方法找到适合的超参数。
• CNN的参数量虽然相对全连接层已经减少了很多，但是还是很大，如果输入是 H×W×3 H × W × 3 的图像，第一个卷积层的卷积核大小为 Nf×Nf N f × N f ， Nfm N f m 个feature map，padding方式为”SAME”，则这两层之间的参数个数为 Nfm×(Nf×Nf×3+1) N f m × ( N f × N f × 3 + 1 ) ，其中1表示每个feature map上的偏置。因此在设计CNN的时候需要考虑其内存占用情况
• 在训练的过程中，为了之后进行反向计算，所有在前向计算时的参数都需要保存，因此一个CNN在训练的过程中需要的RAM与所有层的参数量之和成正比

池化层(pooling layer)

• 池化层主要是对输入图像进行降采样（subsample），为了降低CNN的计算负载、内存使用以及参数量等，这也能够降低CNN过拟合的风险，同时也使得网络具有部分的位移不变性
• 池化层的感受野是一个正方形的区域，它是将上一层的感受野转化为一个值（最大值或者平均值等）
• 池化层是对每个输入层的通道进行单独处理。
• TF中，可以设置池化的size，strides，padding等参数
• TF中，池化的kernel size(ksize)的第一个数必须是1，因为目前TF无法对多个样本做池化，同时无法对三维空间同时做池化，因此第2~4个数中必须有一个为1
• 目前池化层最主要的作用就是减小上一个网络层的尺寸，很少涉及不同feature map之间的交互操作

X = tf.placeholder( tf.float32, shape=(None, height, width, channels) )
max_pool = tf.nn.max_pool( X, ksize=[1,2,2,1], strides=[1,2,2,1], padding="VALID" )

with tf.Session() as sess:
    output = sess.run( max_pool, feed_dict={X:dataset} )

print( dataset.shape )
print( output.shape )

(2, 427, 640, 3)
(2, 213, 320, 3)

• 在CNN使用的过程中，可以避免使用一些过大的卷积核，将其拆分成由若干个小的卷积核组成，可以大大减小参数量

一些典型的网络结构

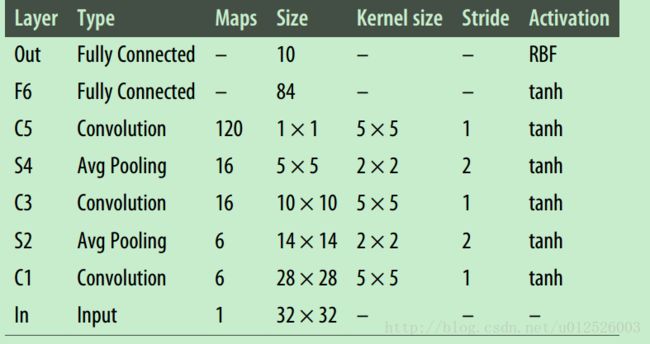
LeNet-5

• 主要包含以下几层
  
  • input -> Convolution -> Avg Pooling -> Convolution -> Avg Pooling -> Convolution -> FC -> FC(output)

AlexNet

• AlexNet是第一个将卷积层之间连接的神经网络（之前LeNet中是CNN之间加入池化层）。结构如下

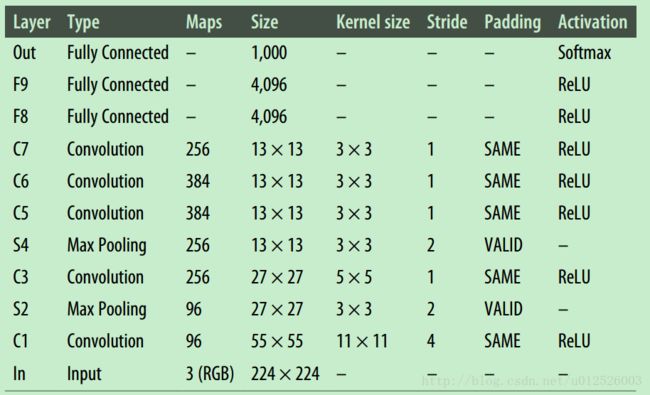
• AlexNet中使用了之前博文中提到的两种正则化方法防止过拟合：dropout与数据增强技术（给图像施加不同的偏移量、水平翻转以及改变图像亮度）
• AlexNet提出了local response normalization(LRN)，对C1和C3的RELU输出结果进行处理，提升了模型的泛化能力。计算方法如下
  
  bi=ai(k+α∑j=max(0,i−r2)min(i+r2,fn−1)a2j)−β b i = a i ( k + α ∑ j = max ( 0 , i − r 2 ) min ( i + r 2 , f n − 1 ) a j 2 ) − β
  
  其中 bi b i 是LRN处理后的输出， ai a i 是RELU激活函数的输出。 k,α,β,r k , α , β , r 都是超参数。
• 注：这个正则化方法可以用其他的正则化方法替代。

GoogleNet

• GoogleNet的网络层比之前的深很多，采用了子网络的结构，是inception module
• inception module中包含很多个很小的卷积核，它们串联之后，作用与大的卷积核相似，但是大大减少了模型的参数量。
• GoogleNet包含了9个inception module，具体的网络结构可以参考：http://blog.csdn.net/marsjhao/article/details/73088850

ResNet

• 之前对DNN的研究中，理论上采用无限深的网络结构可以逼近任意函数，但是由于很深的NN在训练时会遇到梯度弥散的问题，因此效果一般并不好。
• ResNet包含152层的网络结构，采用了shortcut connection的概念，即加入了恒等映射层，输入可以通过网络层处理到达下一层，也可以直接到达下一层，因此网络随着深度的增加，也不会发生退化现象，这解决了深层网络训练过程中的梯度弥散问题。
• 参考链接：https://www.jianshu.com/p/46d76bd56766，http://blog.csdn.net/circleyuanquan/article/details/60875016

TF中一些卷积的操作

• conv1d是1维向量的卷积操作，在NLP等中常被用到。
• conv3d是对3D矩阵做卷积。
• astrous_conv2d：相当于扩大卷积核的大小（中间扩大的部分用0补齐），这可以在不增加额外参数的条件下增大神经元节点的感受野。
• conv2d_transpose：相当于创建deconvolutional layer，这是对图像做升采样（可以认为在卷积过程中stride是小于1的），在segmentation等任务中常常用到
• depthwise_conv2d：对每一个输入的map做处理，如果卷积核设置的为 fn f n 个map，输入是 fn′ f n ′ 个map，则这个卷积操作会输出 fn×fn′ f n × f n ′ 个feature map。
• separable_conv2d：先像depthwise_conv2d那样操作，然后再使用1X1的卷积核做处理，这可以使得不同feature map之间的信息进行交互。

import tensorflow as tf

height = 28
width = 28
channels = 1
n_inputs = height * width

conv1_fmaps = 32
conv1_ksize = 3
conv1_stride = 1
conv1_pad = "SAME"

conv2_fmaps = 64
conv2_ksize = 3
conv2_stride = 1
conv2_pad = "SAME"
conv2_dropout_rate = 0.25

pool3_fmaps = conv2_fmaps

n_fc1 = 128
fc1_dropout_rate = 0.5

n_outputs = 10

reset_graph()

with tf.name_scope("inputs"):
    X = tf.placeholder(tf.float32, shape=[None, n_inputs], name="X")
    X_reshaped = tf.reshape(X, shape=[-1, height, width, channels])
    y = tf.placeholder(tf.int32, shape=[None], name="y")
    training = tf.placeholder_with_default(False, shape=[], name='training')

conv1 = tf.layers.conv2d(X_reshaped, filters=conv1_fmaps, kernel_size=conv1_ksize,
                         strides=conv1_stride, padding=conv1_pad,
                         activation=tf.nn.relu, name="conv1")
conv2 = tf.layers.conv2d(conv1, filters=conv2_fmaps, kernel_size=conv2_ksize,
                         strides=conv2_stride, padding=conv2_pad,
                         activation=tf.nn.relu, name="conv2")

with tf.name_scope("pool3"):
    pool3 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="VALID")
    pool3_flat = tf.reshape(pool3, shape=[-1, pool3_fmaps * 14 * 14])
    pool3_flat_drop = tf.layers.dropout(pool3_flat, conv2_dropout_rate, training=training)

with tf.name_scope("fc1"):
    fc1 = tf.layers.dense(pool3_flat_drop, n_fc1, activation=tf.nn.relu, name="fc1")
    fc1_drop = tf.layers.dropout(fc1, fc1_dropout_rate, training=training)

with tf.name_scope("output"):
    logits = tf.layers.dense(fc1, n_outputs, name="output")
    Y_proba = tf.nn.softmax(logits, name="Y_proba")

with tf.name_scope("train"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=y)
    loss = tf.reduce_mean(xentropy)
    optimizer = tf.train.AdamOptimizer()
    training_op = optimizer.minimize(loss)

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

with tf.name_scope("init_and_save"):
    init = tf.global_variables_initializer()
    saver = tf.train.Saver()

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("./dataset/mnist/")

def get_model_params():
    gvars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES)
    return {gvar.op.name: value for gvar, value in zip(gvars, tf.get_default_session().run(gvars))}

def restore_model_params(model_params):
    gvar_names = list(model_params.keys())
    assign_ops = {gvar_name: tf.get_default_graph().get_operation_by_name(gvar_name + "/Assign")
                  for gvar_name in gvar_names}
    init_values = {gvar_name: assign_op.inputs[1] for gvar_name, assign_op in assign_ops.items()}
    feed_dict = {init_values[gvar_name]: model_params[gvar_name] for gvar_name in gvar_names}
    tf.get_default_session().run(assign_ops, feed_dict=feed_dict)

n_epochs = 10
batch_size = 50


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch, training: True})

        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_val = accuracy.eval(feed_dict={X: mnist.validation.images,
                                           y: mnist.validation.labels})
        print("Epoch {}, train accuracy: {:.4f}%, valid. accuracy: {:.4f}%, valid. best loss: {:.6f}".format(
                  epoch, acc_train * 100, acc_val * 100, best_loss_val))

    acc_test = accuracy.eval(feed_dict={X: mnist.test.images,
                                        y: mnist.test.labels})
    print("Final accuracy on test set:", acc_test)

Extracting ./dataset/mnist/train-images-idx3-ubyte.gz
Extracting ./dataset/mnist/train-labels-idx1-ubyte.gz
Extracting ./dataset/mnist/t10k-images-idx3-ubyte.gz
Extracting ./dataset/mnist/t10k-labels-idx1-ubyte.gz

mnist.validation.labels.shape

(5000,)