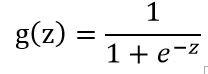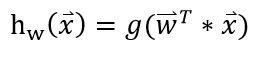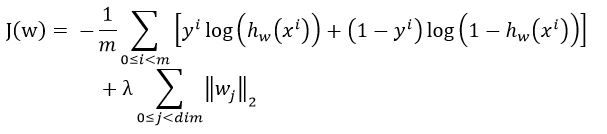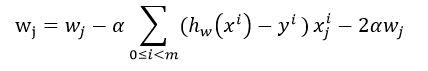快速用梯度下降法实现一个Logistic Regression 分类器

前阵子听说一个面试题：你实现一个logistic Regression需要多少分钟？搞数据挖掘的人都会觉得实现这个简单的分类器分分钟就搞定了吧？

因为我做数据挖掘的时候，从来都是顺手用用工具的，尤其是微软内部的TLC相当强大，各种机器学习的算法都有，于是自从离开学校后就没有自己实现过这些基础的算法。当有一天心血来潮自己实现一个logistic regression的时候，我会说用了3个小时么？。。。羞羞

---------------------------------------------------前言结束----------------------------------------------

 

当然logistic regression的渊源还是有点深的，想复习理论知识的话可以去http://en.wikipedia.org/wiki/Logistic_regression ， 我这里就直接讲实现啦。 

首先要了解一个logistic function

    

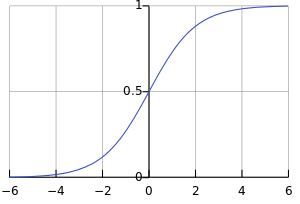
这个函数的图像是这个样子的：

 

而我们要实现的logistic regression model，就是要去学习出一组权值w：

 x 指feature构成的向量。 这个向量w就可以将每个instance映射到一个实数了。

假如我们要出里的是2分类问题，那么问题就被描述为学习出一组w，使得h(正样本)趋近于1， h(负样本)趋近于0.

现在就变成了一个最优化问题，我们要让误差最小化。 现在问题来了，怎么定义误差函数呢？

首先想到的是L2型损失函数啦，于是啪啪啪写上了

。

很久没有复习logistic regression的人最容易犯错的就是在这了。正确的写法是：

，

然后对它求偏导数得到梯度下降法的迭代更新方程：

。

于是你会发现这个迭代方程是和线性回归的是一样的！

理清了过程时候，代码就变得异常简单了：

  1  public class LogisticRegression
  2     {
  3         private int _maxIteration = 1000;
  4         private double _stepSize = 0.000005;
  5         //private double _stepSize = 0.1;
  6         private double _lambda = 0.1;
  7         private double decay = 0.95;
  8 
  9         public int dim;
 10         public double[] theta;
 11 
 12         public LogisticRegression(int dim)
 13         {
 14             this.dim = dim;
 15         }
 16 
 17         public LogisticRegression(int dim, double stepSize)
 18             : this(dim)
 19         {
 20             this._stepSize = stepSize;
 21         }
 22 
 23         public void Train(Instance[] instances)
 24         {
 25             Initialize();
 26 
 27             int instCnt = instances.Length;
 28             double[] dev =new double[this.dim];
 29             for (int t = 0; t < this._maxIteration; t++)
 30             {
 31                 double cost = 0;
 32                 for (int i = 0; i < instCnt; i++)
 33                 {
 34                     double h_x = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
 35                     // calculate cost function
 36                     cost += instances[i].label * Math.Log(h_x) + (1 - instances[i].label) * Math.Log(1 - h_x);
 37                 }
 38                 cost *= -1.0 / instCnt; 
 39                 Console.WriteLine("{0},{1}", t, cost);
 40 
 41                
 42                 for (int i = 0; i < instCnt; i++)
 43                 {
 44                     ResetArray(dev);
 45                     double h_x = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
 46                     double error =   h_x- instances[i].label ;
 47                     for (int j = 0; j < this.dim; j++)
 48                     {
 49                         dev[j] += error*instances[i].featureValues[j] + 2*dev[j]*this._lambda;
 50                         this.theta[j] -= this._stepSize * dev[j] ;
 51                         //BoundaryLimiting(ref this.theta[j], 0, 1);
 52                     }
 53                 }
 54                 //this._stepSize *= decay;
 55                 //if (this._stepSize > 0.000001)
 56                 //{
 57                 //    this._stepSize = 0.000001;
 58                 //}
 59             }
 60         }
 61          
 62         private void BoundaryLimiting(ref double alpha, double lowerbound, double upperbound)
 63         {
 64             if (alpha < lowerbound)
 65             {
 66                 alpha = lowerbound;
 67             }
 68             else if (alpha > upperbound)
 69             {
 70                 alpha = upperbound;
 71             }
 72         }
 73  
 74         public double[] Predict(Instance[] instances)
 75         {
 76             double[] results = new double[instances.Length];
 77             for (int i = 0; i < results.Length; i++)
 78             {
 79                 results[i] = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
 80             }
 81             return results;
 82         }
 83 
 84         private void ResetArray(double[] dev)
 85         {
 86             for (int i = 0; i < dev.Length; i++)
 87             {
 88                 dev[i] = 0;
 89             }
 90         }
 91 
 92         private void Initialize()
 93         {
 94             Random ran = new Random(DateTime.Now.Second);
 95 
 96             this.theta = new double[this.dim];
 97             for (int i = 0; i < this.dim; i++)
 98             {
 99                 this.theta[i] = ran.NextDouble() * 0 ; // initialize theta with a small value
100             }
101         }
102 
103 
104         public static void Test()
105         {
106             LogisticRegression lr = new LogisticRegression(3);
107 
108             List instances = new List();
109             using (StreamReader rd = new StreamReader(@"D:\\local exp\\data.csv"))
110             {
111                 string content = rd.ReadLine();
112                 while ((content = rd.ReadLine()) != null)
113                 {
114                     instances.Add(Instance.ParseInstance(content,','));
115                 }
116             }
117 
118            // MinMaxNormalize(instances); 
119 
120             lr.Train(instances.ToArray()); 
121             
122         }
123 
124         private static void MinMaxNormalize(List instances)
125         {
126             int dim = instances[0].dim;
127             double[] min = new double[dim];
128             double[] max = new double[dim];
129 
130             int instCnt = instances.Count;
131             for (int i = 0; i < instCnt; i++)
132             {
133                 for (int j = 0; j < dim; j++)
134                 {
135                     if (i == 0 || instances[i].featureValues[j] < min[j])
136                     {
137                         min[j] = instances[i].featureValues[j];
138                     }
139                     if (i == 0 || instances[i].featureValues[j] > max[j])
140                     {
141                         max[j] = instances[i].featureValues[j];
142                     }
143                 }
144             }
145 
146 
147             for (int j = 0; j < dim; j++)
148             {
149                 double gap = max[j] - min[j];
150                 if (gap <= 0)
151                 {
152                     continue;
153                 }
154                 for (int i = 0; i < instCnt; i++)
155                 {
156                     instances[i].featureValues[j] = (instances[i].featureValues[j] - min[j]) / gap;
157                 }
158             }
159              
160         }
161     }

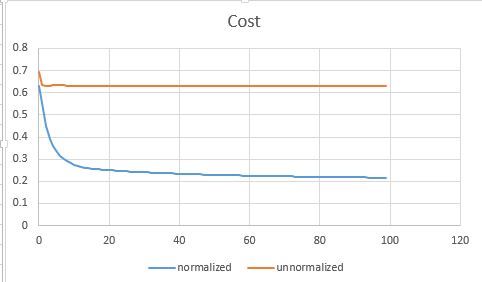
前面提到说我花了3个小时，其中很大一部分原因是在debug算法为啥没有收敛。这里有个很重要的步骤是把feature规范化到[0,1] 。 如果不normalize的话，参数调起来比较麻烦，loss function也经常蹦到NaN去了。

以下是对比normalize和不加normalization的收敛曲线图：

我用的实现数据可以在 http://pingax.com/wp-content/uploads/2013/12/data.csv  下载到。 它是一个2维的数据， 分布如下：

 

转载于:https://www.cnblogs.com/sylvanas2012/p/logisticregression.html