损失函数

1 用于回归的损失函数-残差（Residual） |ŷ−y| | y ^ − y |

令 r=|ŷ−y| r = | y ^ − y |

（1）. L1 Loss

L(r)=r=|ŷ−y| L ( r ) = r = | y ^ − y |

（2）. L2 Loss

平方损失函数是线性回归在假设样本满足高斯分布的条件下推导得到的
L(r)=r2=(ŷ−y)2 L ( r ) = r 2 = ( y ^ − y ) 2
对离群点具有较高的敏感性

（3）. Huber Loss （smooth L1）

L(r)={12r2,σ∗(r−σ2),if r<=σif r>σ L ( r ) = { 1 2 r 2 , if  r <= σ σ ∗ ( r − σ 2 ) , if  r > σ

Huber loss is less sensitive to outliers in data than the squared error loss

2.用于分类的损失函数-余量（Margin） ŷ·y y ^ · y

（1）. 0-1 Loss

L(ŷ,y)={0,1,if ŷ·y>0if ŷ·y<=0 L ( y ^ , y ) = { 0 , if  y ^ · y > 0 1 , if  y ^ · y <= 0
非凸，不连续，求最优解困难
该损失函数的意义就是，当预测错误时，损失函数值为1，预测正确时，损失函数值为0。该损失函数不考虑预测值和真实值的误差程度，也就是只要预测错误，预测错误差一点和差很多是一样的

（2）. 0-1 Margin Loss

L(ŷ,y)={0,1,if ŷ·y>1if ŷ·y<=1 L ( y ^ , y ) = { 0 , if  y ^ · y > 1 1 , if  y ^ · y <= 1

（3）. Hinge Loss

L(ŷ,y)=max(0,1−ŷ·y)={0,1−ŷ·y,if ŷ·y>1if ŷ·y<=1 L ( y ^ , y ) = m a x ( 0 , 1 − y ^ · y ) = { 0 , if  y ^ · y > 1 1 − y ^ · y , if  y ^ · y <= 1
连续凸函数，SVM损失函数

（4）. Log Loss

逻辑回归假设样本服从伯努力分布（0-1分布）
L(Y,P(Y|X))=−log(P(Y|X)) L ( Y , P ( Y | X ) ) = − l o g ( P ( Y | X ) )
连续凸函数，logistic regression的损失函数
L(ŷ,y)=−y·log(ŷ)−（1−y）·log(1−ŷ) L ( y ^ , y ) = − y · l o g ( y ^ ) − （ 1 − y ） · l o g ( 1 − y ^ )
https://blog.csdn.net/wjlucc/article/details/71095206

（5）. Softmax Loss

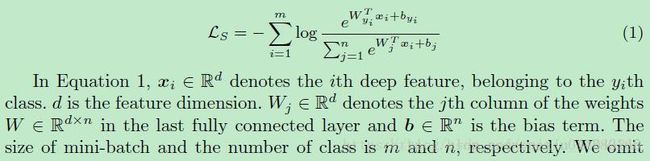
具体见下文：
https://blog.csdn.net/u014380165/article/details/71181256

（6）. Center Loss

是对softmax loss的改进，类间距离变大了，类内距离减少了（主要变化在于类内距离：intra-class）


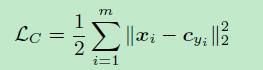
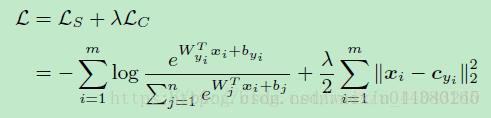
具体见下文：
https://blog.csdn.net/lien0906/article/details/79494565

参考：
https://wenku.baidu.com/view/c93b4dd9b04e852458fb770bf78a6529647d35a7.html
http://www.ituring.com.cn/book/tupubarticle/16827