CNN卷积神经网络学习笔记
对CNN卷积神经网络学习过程中的学习笔记,会持续更新。
本文所说的CNN(Convolution Neural Network)是卷积神经网络的英文首字母,非"美国有线电视新闻网(Cable News Network)"。
CNN结构大同小异,主要由三个部分构成:
1.卷积层(Convlolutional layer)
2.池化层(Pooling layer)
3.全连接层(Full connected layer)
卷积层:
卷积层由多个卷积核构成,卷积核为带有表示权重大小的矩阵。
卷积公式:
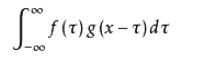
它的物理意义大概可以理解为:系统某一时刻的输出是由多个输入共同作用(叠加)的结果。
放在图像分析里,f(x) 可以理解为原始像素点(source pixel),所有的原始像素点叠加起来,就是原始图了。
g(x)可以称为作用点,所有作用点合起来我们称为卷积核(Convolution kernel)。
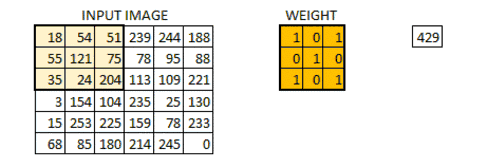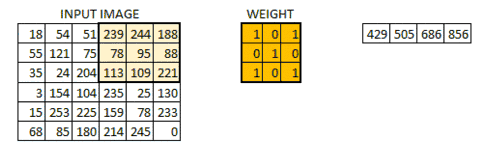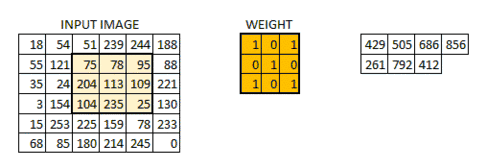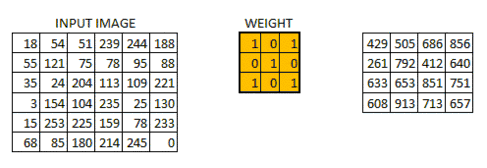
卷积核上所有作用点依次作用于原始像素点后(即乘起来),线性叠加的输出结果,即是最终卷积的输出,也是我们想要的结果,我们称为destination pixel.
卷积过程动态图
卷积的意义:
提取特征。
卷积后输出单元数量计算:
一个输出单元的大小有以下三个量控制:depth, stride 和 zero-padding。
- 深度(depth) : 顾名思义,它控制输出单元的深度,也就是filter的个数,连接同一块区域的神经元个数。又名:depth column
- 步幅(stride):它控制在同一深度的相邻两个隐含单元,与他们相连接的输入区域的距离。如果步幅很小(比如 stride = 1)的话,相邻隐含单元的输入区域的重叠部分会很多; 步幅很大则重叠区域变少。
- 补零(zero-padding) : 我们可以通过在输入单元周围补零来改变输入单元整体大小,从而控制输出单元的空间大小。
输出单元数量计算定义如下:
- : 输入单元的大小(宽或高)
- : 感受野(receptive field)
- : 步幅(stride)
- : 补零(zero-padding)的数量
- : 深度,输出单元的深度
则可以用以下公式计算一个维度(宽或高)内一个输出单元里可以有几个隐藏单元:
如果计算结果不是一个整数,则说明现有参数不能正好适合输入,步幅(stride)设置的不合适,或者需要补零。
池化层:
池化主要方式:
1) mean-pooling,即对邻域内特征点只求平均,对背景保留更好;
2) max-pooling,即对邻域内特征点取最大,对纹理提取更好;
3) Stochastic-pooling,介于两者之间,通过对像素点按照数值大小赋予概率,再按照概率进行亚采样;
作用:
1. invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度)
2. 获得定长输出。(文本分类的时候输入是不定长的,可以通过池化获得定长输出)
3. 保留主要的特征同时减少参数(降维,效果类似PCA)和计算量,防止过拟合,提高模型泛化能力
做窗口滑动卷积的时候,卷积值就代表了整个窗口的特征。因为滑动的窗口间有大量重叠区域,出来的卷积值有冗余,进行最大pooling或者平均pooling就是减少冗余。
全连接层:
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用,大大减少特征位置对分类带来的影响。因为空间结构特性被忽略了,所以全连接层不适合用于在方位上找Pattern的任务,比如segmentation。
泰勒公式 用多项式函数去拟合光滑函数,全连接层中一层的一个神经元就可以看成一个多项式;用一层fully connected layer 有时候没法解决非线性问题,而如果有两层或以上fully connected layer就可以很好地解决非线性问题了。
在实际使用中,全连接层可由卷积操作实现:对前层是全连接的全连接层可以转化为卷积核为1x1的卷积;而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积,h和w分别为前层卷积结果的高和宽
以VGG-16为例,对224x224x3的输入,最后一层卷积可得输出为7x7x512,如后层是一层含4096个神经元的FC,则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程,其中该卷积核参数如下:
“filter size = 7, padding = 0, stride = 1, D_in = 512, D_out = 4096”
经过此卷积操作后可得输出为1x1x4096。
如需再次叠加一个2048的FC,则可设定参数为“filter size = 1, padding = 0, stride = 1, D_in = 4096, D_out = 2048”的卷积层操作[2]。
CNN训练过程:
损失函数:
如何缩小loss:
解决办法:
反向传播算法
为了达到预测的标签和训练标签一致的目的,需要最小化损失。把最小化损失看作微积分中的一个优化问题,找出时哪些输入直接导致了网络中的损失。
转发传递、丢失功能、反向传递和参数更新的过程是一个训练迭代。这个程序将重复这个过程,为每组训练图像(通常称为批处理)进行固定次数的迭代。一旦在上一个培训示例中完成了参数更新,希望网络应该得到足够的训练,从而使各个层的权重得到正确的调优。
参考文献
[1].CNN网络的pooling层有什么用? - 知乎https://www.zhihu.com/question/36686900
[2].全连接层的作用是什么? - 蒋竺波的回答 - 知乎https://www.zhihu.com/question/41037974/answer/320267531