卡尔曼滤波系列——(三)粒子滤波(重写)
目录
- 1 简介
- 2 原理
- 2.1 贝叶斯推断中的蒙特卡洛近似
- 2.2 重要性采样
- 2.3 序贯重要性采样
- 2.4 序贯重要性重采样
- 3 实验
- 4 总结
- 5 参考文献
1 简介
尽管对于大多数滤波问题中,采用高斯近似的方式(例如卡尔曼滤波和扩展卡尔曼滤波方法)可以很好地解决。但是对于多模式或者状态量是离散的这样的滤波问题,高斯近似并不合适;而对于非线性问题,扩展卡尔曼滤波在做局部线性化的操作时,同样损失了一定的精度,模型的非线性度越强,损失得越多。
在这样的情况下,基于序贯重要性采样方法的例子滤波(Partical Filter,PF)是一个有效的替代方法,它通过蒙特卡洛近似的方式获得贝叶斯滤波问题中后验分布的解,从而达到滤波或者状态估计的目的。
2 原理
2.1 贝叶斯推断中的蒙特卡洛近似
在贝叶斯推断中,包括贝叶斯滤波,主要的问题通常集中在后验分布的期望计算,如下所示:
E [ f ( θ ) ∣ z 1 : k ] = ∫ f ( θ ) p ( θ ∣ z 1 : k ) d θ {\bf{E}}[{\bf{f}}\left( {\bf{\theta }} \right)|{{\bf{z}}_{1:k}}]{\rm{ }} = \int {{\bf{f}}\left( {\bf{\theta }} \right)p\left( {{{\bf{\theta }}}|{{\bf{z}}_{1:k}}} \right)d{{\bf{\theta }}}} E[f(θ)∣z1:k]=∫f(θ)p(θ∣z1:k)dθ
其中 f \bf{f} f表示从 R N → R M \mathbb{R}^{N}\rightarrow \mathbb{R}^{M} RN→RM的任意函数,而 p ( θ ∣ z 1 : k ) p\left( {{{\bf{\theta }}}|{{\bf{z}}_{1:k}}} \right) p(θ∣z1:k)表示给定观测 z 1 : k {\bf{z}}_{1:k} z1:k下状态 θ {\bf{\theta }} θ的后验概率密度函数。现在的问题是这样的积分只有在一些特殊情况中会获得闭合解,在多数情况下,需要用到数值方法求解,蒙特卡洛采样就是常用的数值解法。
蒙特卡洛采样指的是从后验分布中采样后取平均以估计统计量,从而代替闭合解的求取。
根据后验分布 p ( θ ∣ z 1 : k ) p\left( {{{\bf{\theta }}}|{{\bf{z}}_{1:k}}} \right) p(θ∣z1:k)取 S S S个采样 θ ( s ) {{\bf{\theta }}^{(s)}} θ(s), θ ( s ) ∼ p ( θ ∣ z 1 : k ) , s = 1 , . . . , S {{\bf{\theta }}^{(s)}} \sim p\left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right),s = 1,...,S θ(s)∼p(θ∣z1:k),s=1,...,S,于是可以用下式估计期望
E [ f ( θ ) ∣ z 1 : k ] ≈ 1 S ∑ s = 1 S f ( θ ( s ) ) {\bf{E}}[{\bf{f}}\left( {\bf{\theta }} \right)|{{\bf{z}}_{1:k}}]{\rm{ }} \approx \frac{1}{S}\sum\limits_{s = 1}^S {{\bf{f}}\left( {{{\bf{\theta }}^{(s)}}} \right)} E[f(θ)∣z1:k]≈S1s=1∑Sf(θ(s))
2.2 重要性采样
然而,在实际情况中, p ( θ ∣ z 1 : k ) p\left( {{{\bf{\theta }}}|{{\bf{z}}_{1:k}}} \right) p(θ∣z1:k)取 S S S个采样 θ ( s ) {{\bf{\theta }}^{(s)}} θ(s) 的方程形式复杂,几乎不可能直接从该后验分布中获得采样,所以选择使用重要性采样(Importance Sampling, IS)分布 π ( θ ∣ z 1 : k ) \pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right) π(θ∣z1:k)来近似后验分布,从该分布中获取采样相对简单。
E [ f ( θ ) ∣ z 1 : k ] = ∫ f ( θ ) p ( θ ∣ z 1 : k ) π ( x ∣ z 1 : k ) π ( θ ∣ z 1 : k ) d θ = ∫ f ( θ ) p ( z 1 : k ∣ θ ) p ( θ ) p ( z 1 : k ) π ( θ ∣ z 1 : k ) π ( θ ∣ z 1 : k ) d θ = ∫ f ( θ ) p ( z 1 : k ∣ θ ) p ( θ ) π ( θ ∣ z 1 : k ) π ( θ ∣ z 1 : k ) d θ ∫ p ( z 1 : k ∣ θ ) p ( θ ) π ( θ ∣ z 1 : k ) π ( θ ∣ z 1 : k ) d θ {\bf{E}}[{\bf{f}}\left( {\bf{\theta }} \right)\left| {{{\bf{z}}_{1:k}}} \right.] = \int {\bf{f}} \left( {\bf{\theta }} \right)\frac{{p\left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)}}{{{\bf{\pi }}\left( {{\bf{x}}|{{\bf{z}}_{1:k}}} \right)}}{\bf{\pi }}\left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}\\ = \int {\bf{f}} \left( {\bf{\theta }} \right)\frac{{p\left( {{{\bf{z}}_{1:k}}|{\bf{\theta }}} \right)p\left( {\bf{\theta }} \right)}}{{p\left( {{{\bf{z}}_{1:k}}} \right)\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)}}\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}\\ = \frac{{\int {\bf{f}} \left( {\bf{\theta }} \right)\frac{{p\left( {{{\bf{z}}_{1:k}}|{\bf{\theta }}} \right)p\left( {\bf{\theta }} \right)}}{{\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)}}\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}}}{{\int {\frac{{p\left( {{{\bf{z}}_{1:k}}|{\bf{\theta }}} \right)p\left( {\bf{\theta }} \right)}}{{\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)}}} \pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}}} E[f(θ)∣z1:k]=∫f(θ)π(x∣z1:k)p(θ∣z1:k)π(θ∣z1:k)dθ=∫f(θ)p(z1:k)π(θ∣z1:k)p(z1:k∣θ)p(θ)π(θ∣z1:k)dθ=∫π(θ∣z1:k)p(z1:k∣θ)p(θ)π(θ∣z1:k)dθ∫f(θ)π(θ∣z1:k)p(z1:k∣θ)p(θ)π(θ∣z1:k)dθ
如果我们用 ω \omega ω表示 p ( z 1 : k ∣ θ ) p ( θ ) π ( θ ∣ z 1 : k ) \frac{{p\left( {{{\bf{z}}_{1:k}}|{\bf{\theta }}} \right)p\left( {\bf{\theta }} \right)}}{{\pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)}} π(θ∣z1:k)p(z1:k∣θ)p(θ),再利用蒙特卡洛方法,就能获得下式:
E [ f ( θ ) ∣ z 1 : k ] = ∫ f ( θ ) ω π ( θ ∣ z 1 : k ) d θ ∫ ω π ( θ ∣ z 1 : k ) d θ ≈ ∑ s = 1 S f ( θ ( s ) ) ω ( s ) ∑ s = 1 S ω ( s ) {\bf{E}}[{\bf{f}}\left( {\bf{\theta }} \right)\left| {{{\bf{z}}_{1:k}}} \right.] = \frac{{\int {\bf{f}} \left( {\bf{\theta }} \right)\omega \pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}}}{{\int \omega \pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right)d{\bf{\theta }}}} \approx \frac{{\sum\limits_{s = 1}^S {\bf{f}} \left( {{{\bf{\theta }}^{\left( s \right)}}} \right){\omega ^{(s)}}}}{{\sum\limits_{s = 1}^S {{\omega ^{(s)}}} }} E[f(θ)∣z1:k]=∫ωπ(θ∣z1:k)dθ∫f(θ)ωπ(θ∣z1:k)dθ≈s=1∑Sω(s)s=1∑Sf(θ(s))ω(s)
于是有了重要性采样粒子滤波算法。给定观测模型 p ( z 1 : k ∣ θ ) p\left( {{{\bf{z}}_{1:k}}|{\bf{\theta }}} \right) p(z1:k∣θ)和先验 p ( θ ) p\left( {\bf{\theta }} \right) p(θ),可以将后验用重要性采样近似如下:
-
从重要性分布采样得到 S S S个粒子:
θ ( s ) ∼ π ( θ ∣ z 1 : k ) , s = 1 , . . . , S {{\bf{\theta }}^{(s)}} \sim \pi \left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right),s = 1,...,S θ(s)∼π(θ∣z1:k),s=1,...,S -
计算未归一化的粒子权重 ω ∗ ( s ) {\omega ^{*(s)}} ω∗(s):
ω ∗ ( s ) = p ( z 1 : k ∣ θ ( s ) ) p ( θ ( s ) ) π ( θ ( s ) ∣ z 1 : k ) {\omega ^{*(s)}} = \frac{{p\left( {{{\bf{z}}_{1:k}}|{{\bf{\theta }}^{(s)}}} \right)p\left( {{{\bf{\theta }}^{(s)}}} \right)}}{{\pi \left( {{{\bf{\theta }}^{(s)}}|{{\bf{z}}_{1:k}}} \right)}} ω∗(s)=π(θ(s)∣z1:k)p(z1:k∣θ(s))p(θ(s))
然后归一化权重得到
ω ( s ) = ω ∗ ( s ) ∑ i = 1 S ω ( i ) {\omega ^{(s)}} = \frac{{{\omega ^{*(s)}}}}{{\sum\limits_{i = 1}^S {{\omega ^{(i)}}} }} ω(s)=i=1∑Sω(i)ω∗(s) -
于是 f ( θ ) {\bf{f}}\left( {\bf{\theta }} \right) f(θ)的后验期望可以用下式近似
E [ f ( θ ) ∣ z 1 : k ] ≈ ∑ s = 1 S f ( θ ( s ) ) ω ( s ) {\bf{E}}[{\bf{f}}\left( {\bf{\theta }} \right)\left| {{{\bf{z}}_{1:k}}} \right.] \approx \sum\limits_{s = 1}^S {\bf{f}} \left( {{{\bf{\theta }}^{\left( s \right)}}} \right){\omega ^{(s)}} E[f(θ)∣z1:k]≈s=1∑Sf(θ(s))ω(s)
上述算法所描述的后验概率密度可以写成如下形式:
p ( θ ∣ z 1 : k ) ≈ ∑ s = 1 S ω ( s ) δ ( θ − θ ( s ) ) p\left( {{\bf{\theta }}|{{\bf{z}}_{1:k}}} \right) \approx \sum\limits_{s = 1}^S {{\omega ^{(s)}}\delta \left( {{\bf{\theta }} - {{\bf{\theta }}^{(s)}}} \right)} p(θ∣z1:k)≈s=1∑Sω(s)δ(θ−θ(s))
其中 δ ( ⋅ ) \delta \left( \cdot \right) δ(⋅)表示狄利克雷函数。
2.3 序贯重要性采样
序贯重要性采样(Sequential importance sampling,SIS)是序贯版本的重要性采样,SIS算法可用于生成重要性采样近似值,以滤波形式如下的通用状态空间模型的分布,状态转移方程和观测方程如下:
θ k = f ( θ k − 1 ) + s k {{\bf{\theta }}_k} = {\bf{f}}\left( {{{\bf{\theta }}_{k - 1}}} \right) + {{\bf{s}}_k} θk=f(θk−1)+sk
z k = h ( θ k ) + v k {{\bf{z}}_k} = {\bf{h}}\left( {{{\bf{\theta }}_k}} \right) + {{\bf{v}}_k} zk=h(θk)+vk
其中 θ k {\bf{\theta }}_k θk表示第 k {k} k时刻的系统状态, z k {\bf{z}}_k zk表示对 k {k} k时刻系统状态的观测结果,而 f ( ⋅ ) {\bf{f}}( \cdot ) f(⋅)和 h ( ⋅ ) {\bf{h}}( \cdot ) h(⋅)分别代表状态转移函数和观测函数,另外 s k {\bf{s}}_k sk为状态噪声, s k ∼ N ( 0 , Q ) {{\bf{s}}_k}\sim N\left( {{\bf{0}},{\bf{Q}}} \right) sk∼N(0,Q), r k {{\bf{r}}_k} rk为观测噪声, r k ∼ N ( 0 , R ) {{\bf{r}}_k}\sim N\left( {{\bf{0}},{\bf{R}}} \right) rk∼N(0,R)。滤波问题在于如何利用传感器的观测 z k {{\bf{z}}_k} zk,实现对系统状态 θ k {{\bf{\theta }}_k} θk更准确的估计。
考虑给定观测 z 1 : k {{\bf{z}}_{1:k}} z1:k的条件下所有状态 θ 0 : k {{\bf{\theta }}_{0:k}} θ0:k的完整后验分布,利用模型的Markov性质,可以得到如下后验分布的递推公式:
p ( θ 0 : k ∣ z 1 : k ) ∝ p ( z k ∣ θ 0 : k , z 1 : k − 1 ) p ( θ 0 : k ∣ z 1 : k − 1 ) = p ( z k ∣ θ k , z 1 : k − 1 ) p ( θ k ∣ θ 0 : k − 1 , z 1 : k − 1 ) p ( θ 0 : k − 1 ∣ z 1 : k − 1 ) = p ( z k ∣ θ k ) p ( θ k ∣ θ k − 1 ) p ( θ 0 : k − 1 ∣ z 1 : k − 1 ) p\left( {{{\bf{\theta }}_{0:k}}|{{\bf{z}}_{1:k}}} \right) \propto p\left( {{{\bf{z}}_k}|{{\bf{\theta }}_{0:k}},{{\bf{z}}_{1:k - 1}}} \right)p\left( {{{\bf{\theta }}_{0:k}}|{{\bf{z}}_{1:k - 1}}} \right)\\ = p\left( {{{\bf{z}}_k}|{{\bf{\theta }}_k},{{\bf{z}}_{1:k - 1}}} \right)p\left( {{{\bf{\theta }}_k}|{{\bf{\theta }}_{0:k - 1}},{{\bf{z}}_{1:k - 1}}} \right)p\left( {{{\bf{\theta }}_{0:k - 1}}|{{\bf{z}}_{1:k - 1}}} \right)\\ = p\left( {{{\bf{z}}_k}|{{\bf{\theta }}_k}} \right)p\left( {{{\bf{\theta }}_k}|{{\bf{\theta }}_{k - 1}}} \right)p\left( {{{\bf{\theta }}_{0:k - 1}}|{{\bf{z}}_{1:k - 1}}} \right) p(θ0:k∣z1:k)∝p(zk∣θ0:k,z1:k−1)p(θ0:k∣z1:k−1)=p(zk∣θk,z1:k−1)p(θk∣θ0:k−1,z1:k−1)p(θ0:k−1∣z1:k−1)=p(zk∣θk)p(θk∣θk−1)p(θ0:k−1∣z1:k−1)
因此,粒子的重要性权重可以用下式计算
ω k ( s ) ∝ p ( z k ∣ θ k ( s ) ) p ( θ k ( s ) ∣ θ k − 1 ( s ) ) p ( θ 0 : k − 1 ( s ) ∣ z 1 : k − 1 ) π ( θ 0 : k ( s ) ∣ z 1 : k ) \omega _k^{(s)} \propto \frac{{p\left( {{{\bf{z}}_k}|{\bf{\theta }}_k^{(s)}} \right)p\left( {{\bf{\theta }}_k^{(s)}|{\bf{\theta }}_{k - 1}^{(s)}} \right)p\left( {{\bf{\theta }}_{0:k - 1}^{(s)}|{{\bf{z}}_{1:k - 1}}} \right)}}{{\pi \left( {{\bf{\theta }}_{0:k}^{(s)}|{{\bf{z}}_{1:k}}} \right)}} ωk(s)∝π(θ0:k(s)∣z1:k)p(zk∣θk(s))p(θk(s)∣θk−1(s))p(θ0:k−1(s)∣z1:k−1)
如果构造的重要性采样满足下列关系
π ( θ 0 : k ∣ z 1 : k ) = π ( θ k ∣ θ 0 : k − 1 z 1 : k ) π ( θ 0 : k − 1 ∣ z 1 : k − 1 ) \pi \left( {{{\bf{\theta }}_{0:k}}|{{\bf{z}}_{1:k}}} \right) = \pi \left( {{{\bf{\theta }}_k}|{{\bf{\theta }}_{0:k - 1}}{{\bf{z}}_{1:k}}} \right)\pi \left( {{{\bf{\theta }}_{0:k - 1}}|{{\bf{z}}_{1:k - 1}}} \right) π(θ0:k∣z1:k)=π(θk∣θ0:k−1z1:k)π(θ0:k−1∣z1:k−1)
那么可以获得以下粒子权重的递推关系式
ω k ( s ) ∝ p ( z k ∣ θ k ( s ) ) p ( θ k ( s ) ∣ θ k − 1 ( s ) ) π ( θ k ( s ) ∣ θ 0 : k − 1 ( s ) , z 1 : k ) p ( θ 0 : k − 1 ( s ) ∣ z 1 : k − 1 ) π ( θ 0 : k − 1 ( s ) ∣ z 1 : k − 1 ) ∝ p ( z k ∣ θ k ( s ) ) p ( θ k ( s ) ∣ θ k − 1 ( s ) ) π ( θ k ( s ) ∣ θ 0 : k − 1 ( s ) , z 1 : k ) ω k − 1 ( s ) \omega _k^{(s)} \propto \frac{{p\left( {{{\bf{z}}_k}|{\bf{\theta }}_k^{(s)}} \right)p\left( {{\bf{\theta }}_k^{(s)}|{\bf{\theta }}_{k - 1}^{(s)}} \right)}}{{\pi \left( {{\bf{\theta }}_k^{(s)}|{\bf{\theta }}_{0:k - 1}^{(s)},{{\bf{z}}_{1:k}}} \right)}}\frac{{p\left( {{\bf{\theta }}_{0:k - 1}^{(s)}|{{\bf{z}}_{1:k - 1}}} \right)}}{{\pi \left( {{\bf{\theta }}_{0:k - 1}^{(s)}|{{\bf{z}}_{1:k - 1}}} \right)}}\\ \propto \frac{{p\left( {{{\bf{z}}_k}|{\bf{\theta }}_k^{(s)}} \right)p\left( {{\bf{\theta }}_k^{(s)}|{\bf{\theta }}_{k - 1}^{(s)}} \right)}}{{\pi \left( {{\bf{\theta }}_k^{(s)}|{\bf{\theta }}_{0:k - 1}^{(s)},{{\bf{z}}_{1:k}}} \right)}}\omega _{k - 1}^{(s)} ωk(s)∝π(θk(s)∣θ0:k−1(s),z1:k)p(zk∣θk(s))p(θk(s)∣θk−1(s))π(θ0:k−1(s)∣z1:k−1)p(θ0:k−1(s)∣z1:k−1)∝π(θk(s)∣θ0:k−1(s),z1:k)p(zk∣θk(s))p(θk(s)∣θk−1(s))ωk−1(s)
更进一步地,可以选取重要性采样如下
π ( θ k ∣ θ 0 : k − 1 , z 1 : k ) = p ( θ k ∣ θ k − 1 ) \pi \left( {{{\bf{\theta }}_k}|{{\bf{\theta }}_{0:k - 1}},{{\bf{z}}_{1:k}}} \right) = p\left( {{{\bf{\theta }}_k}|{{\bf{\theta }}_{k - 1}}} \right) π(θk∣θ0:k−1,z1:k)=p(θk∣θk−1)
那么粒子权重的递推关系式可简化为
ω k ( s ) ∝ p ( z k ∣ θ k ( s ) ) ω k − 1 ( s ) \omega _k^{(s)} \propto p\left( {{{\bf{z}}_k}|{\bf{\theta }}_k^{(s)}} \right)\omega _{k - 1}^{(s)} ωk(s)∝p(zk∣θk(s))ωk−1(s)
于是有了序贯重要性采样粒子滤波算法如下:
-
从 k k k时刻的序贯重要性分布采样得到 S S S个粒子:
θ k ( s ) ∼ p ( θ k ∣ θ k − 1 ( s ) ) , s = 1 , . . . , S {\bf{\theta }}_k^{(s)} \sim p\left( {{{\bf{\theta }}_k}|{\bf{\theta }}_{k - 1}^{(s)}} \right),s = 1,...,S θk(s)∼p(θk∣θk−1(s)),s=1,...,S -
计算未归一化的粒子权重 ω ∗ ( s ) {\omega ^{*(s)}} ω∗(s):
ω k ∗ ( s ) = p ( z k ∣ θ k ( s ) ) \omega _k^{*(s)} = p\left( {{{\bf{z}}_k}|{\bf{\theta }}_k^{(s)}} \right) ωk∗(s)=p(zk∣θk(s))
然后归一化权重得到
ω k ( s ) = ω k ∗ ( s ) ∑ i = 1 S ω k ( i ) \omega _k^{(s)} = \frac{{\omega _k^{*(s)}}}{{\sum\limits_{i = 1}^S {\omega _k^{(i)}} }} ωk(s)=i=1∑Sωk(i)ωk∗(s) -
于是 f ( θ k ) {\bf{f}}\left( {{{\bf{\theta }}_k}} \right) f(θk)的后验期望可以用下式近似
E [ f ( θ k ) ∣ z 1 : k ] ≈ ∑ s = 1 S f ( θ k ( s ) ) ω k ( s ) {\bf{E}}[{\bf{f}}\left( {{{\bf{\theta }}_k}} \right)\left| {{{\bf{z}}_{1:k}}} \right.] \approx \sum\limits_{s = 1}^S {\bf{f}} \left( {{\bf{\theta }}_k^{\left( s \right)}} \right)\omega _k^{(s)} E[f(θk)∣z1:k]≈s=1∑Sf(θk(s))ωk(s)
2.4 序贯重要性重采样
上一节中描述的SIS算法中的一个问题是,我们很容易遇到几乎所有粒子的权重为零或接近零的情况。这在粒子过滤文献中被称为简并性问题,它阻止了粒子过滤器多年的实际应用。
退化问题可以通过使用重采样过程来解决。它是指从权重定义的离散分布中提取 S S S个新样本,并用该新集合替换 S S S个样本的旧集合的过程。此重采样过程可以表示为以下算法:
- 将每个权重 ω k ( s ) \omega _k^{(s)} ωk(s)作为从集合 { θ k ( s ) : s = 1 , . . . , S } \left\{ {\theta _k^{(s)}:s = 1,...,S} \right\} {θk(s):s=1,...,S}中抽到索引为 s s s粒子的概率;
- 从该离散分布中抽取 S S S个样本,并用新样本集替换旧样本集;
- 把所有粒子的权重设置为常数: ω k ( s ) = 1 S \omega _k^{(s)} = \frac{1}{S} ωk(s)=S1
基于以上重采样方法,结合序贯重要性采样粒子滤波,得到序贯重要性重采样粒子滤波算法:
-
从 k k k时刻的序贯重要性分布采样得到 S S S个粒子:
θ ~ k ( s ) ∼ p ( θ k ∣ θ k − 1 ( s ) ) , s = 1 , . . . , S {\bf{\tilde \theta }}_k^{(s)} \sim p\left( {{{\bf{\theta }}_k}|{\bf{\theta }}_{k - 1}^{(s)}} \right),s = 1,...,S θ~k(s)∼p(θk∣θk−1(s)),s=1,...,S -
计算未归一化的粒子权重 ω k ∗ \omega _k^* ωk∗:
ω k ∗ ( s ) = p ( z k ∣ θ ~ k ( s ) ) \omega _k^{*(s)} = p\left( {{{\bf{z}}_k}|{\bf{\tilde \theta }}_k^{(s)}} \right) ωk∗(s)=p(zk∣θ~k(s))
然后归一化权重得到
ω ~ k ( s ) = ω k ∗ ( s ) ∑ i = 1 S ω k ( i ) \tilde \omega _k^{(s)} = \frac{{\omega _k^{*(s)}}}{{\sum\limits_{i = 1}^S {\omega _k^{(i)}} }} ω~k(s)=i=1∑Sωk(i)ωk∗(s) -
从原始粒子集合 { θ ~ k ( s ) , ω ~ ( s ) } , s = 1 , . . . , S \left\{ {{\bf{\tilde \theta }}_k^{(s)},{{\tilde \omega }^{(s)}}} \right\},s = 1,...,S {θ~k(s),ω~(s)},s=1,...,S中重采样,获得新的权重均为 1 S \frac{1}{S} S1的粒子集合为 { θ k ( s ) } , s = 1 , . . . , S \left\{ {{\bf{\theta }}_k^{(s)}} \right\},s = 1,...,S {θk(s)},s=1,...,S;
-
于是 f ( θ k ) {\bf{f}}\left( {{{\bf{\theta }}_k}} \right) f(θk)的后验期望可以用下式近似
E [ f ( θ k ) ∣ z 1 : k ] ≈ 1 S ∑ s = 1 S f ( θ k ( s ) ) {\bf{E}}[{\bf{f}}\left( {{{\bf{\theta }}_k}} \right)\left| {{{\bf{z}}_{1:k}}} \right.] \approx \frac{1}{S}\sum\limits_{s = 1}^S {\bf{f}} \left( {{\bf{\theta }}_k^{\left( s \right)}} \right) E[f(θk)∣z1:k]≈S1s=1∑Sf(θk(s))
3 实验
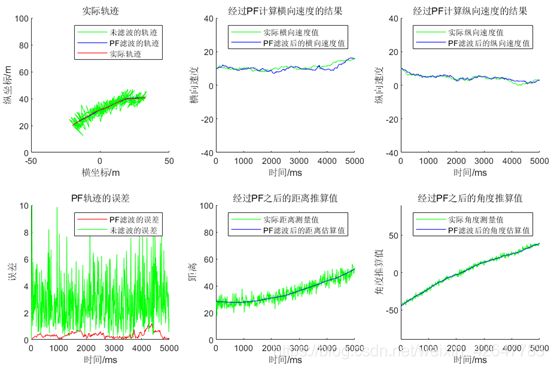
假设一辆车子在空旷场地上行驶,通过毫米波雷达测量车子实时相对于雷达的距离、方位角和径向速度,之后通过该观测结果,估计该车辆的实时状态(包括相对横纵坐标、相对横纵向速度)。
车子的实时状态用 [ x , y , x ˙ , y ˙ ] T {\left[ {x,y,\dot x,\dot y} \right]^T} [x,y,x˙,y˙]T表示,观测量用 [ r , θ , v ] T {\left[ {r,\theta ,v} \right]^T} [r,θ,v]T表示,有以下状态转移方程和观测方程:
[ x k y k x ˙ k y ˙ k ] = f ( [ x k − 1 y k − 1 x ˙ k − 1 y ˙ k − 1 ] ) + s k = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] [ x k − 1 y k − 1 x ˙ k − 1 y ˙ k − 1 ] + s k {\begin{bmatrix} {{x_k}}\\ {{y_k}}\\ {{{\dot x}_k}}\\ {{{\dot y}_k}} \end{bmatrix}} = \bf{f}({\begin{bmatrix} {{x_{k - 1}}}\\ {{y_{k - 1}}}\\ {{{\dot x}_{k - 1}}}\\ {{{\dot y}_{k - 1}}} \end{bmatrix}}) + {{\bf{s}}_k} = {\begin{bmatrix} 1&0&{\Delta t}&0\\ 0&1&0&{\Delta t}\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix}} {\begin{bmatrix} {{x_{k - 1}}}\\ {{y_{k - 1}}}\\ {{{\dot x}_{k - 1}}}\\ {{{\dot y}_{k - 1}}} \end{bmatrix}} + {{\bf{s}}_k} ⎣⎢⎢⎡xkykx˙ky˙k⎦⎥⎥⎤=f(⎣⎢⎢⎡xk−1yk−1x˙k−1y˙k−1⎦⎥⎥⎤)+sk=⎣⎢⎢⎡10000100Δt0100Δt01⎦⎥⎥⎤⎣⎢⎢⎡xk−1yk−1x˙k−1y˙k−1⎦⎥⎥⎤+sk
[ r k θ k v k ] = h ( [ x k y k x ˙ k y ˙ k ] ) + v k = [ x k 2 + x y 2 arctan y k x k x k x ˙ k + y k y ˙ k x k 2 + x y 2 ] {\begin{bmatrix} {{r_k}}\\ {{\theta _k}}\\ {{v_k}} \end{bmatrix}} = h( {\begin{bmatrix} {{x_k}}\\ {{y_k}}\\ {{{\dot x}_k}}\\ {{{\dot y}_k}} \end{bmatrix}}) + {{\bf{v}}_k} = {\begin{bmatrix} {\sqrt {x_k^2 + x_y^2} }\\ {\arctan \frac{{{y_k}}}{{{x_k}}}}\\ {\frac{{{x_k}{{\dot x}_k} + {y_k}{{\dot y}_k}}}{{\sqrt {x_k^2 + x_y^2} }}} \end{bmatrix}} ⎣⎡rkθkvk⎦⎤=h(⎣⎢⎢⎡xkykx˙ky˙k⎦⎥⎥⎤)+vk=⎣⎢⎢⎡xk2+xy2arctanxkykxk2+xy2xkx˙k+yky˙k⎦⎥⎥⎤
给定毫米波雷达观测目标距离的噪声均值为0,方差为10(单位米),观测方位角的噪声均值为0,方差为0.001(单位弧度),测量径向速度的噪声均值为0,方差为2(单位m/s);采样时间点为500个,采样的时间间隔 Δ t = 0.01 \Delta t = 0.01 Δt=0.01秒。
车辆的初始状态为 [ − 20 , 20 , 10 , 10 ] T {\left[ {{\rm{ - 20,20,10,10}}} \right]^T} [−20,20,10,10]T,四个状态量的噪声的方差分别为 [ 0 . 01 , 0 . 01 , 0 . 05 , 0 . 05 ] \left[ {{\rm{0}}{\rm{.01,0}}{\rm{.01,0}}{\rm{.05,0}}{\rm{.05}}} \right] [0.01,0.01,0.05,0.05]。仿真结果图1和图2所示:
4 总结
可以看到,相对于直接取用雷达观测得到的距离和方位角换算出结果作为目标状态的估计而言,通过粒子滤波后获得的状态估计要更加准确,状态波动小,较为稳定,更符合实际中车辆的行驶过程。
本次实验中,通过扩展卡尔曼滤波技术确定的定位均方误差约为0.17m2,而直接用观测结果的定位均方误差为11.1m2,可以看出粒子滤波在定位精度上可以带来极大地提升。
基于序贯重要性重采样的粒子滤波算法的核心在于利用蒙特卡洛方法求解后验期望,其重要性采样选取状态空间的转移概率,使得粒子的递推求解过程非常简便,并做了粒子的重采样,保证了粒子的高效性,也进一步地简化粒子的递推过程。
在给定的状态空间转移和观测模型下,粒子滤波算法的主要思想体现在通过若干粒子模拟系统的真实状态,如果某粒子的观测结果与实际观测很接近,那么该粒子就会获得高权重,反之粒子获得低权重。之后通过重采样的方式筛除低权重粒子,保留高权重的粒子。最后所有粒子共同决定对当前时刻系统状态的估计结果,能够起到抑制噪声的目的。
相比于扩展卡尔曼滤波,粒子滤波通过蒙特卡洛采样的方式近似后验分布,而不用做线性化,因此不会因为线性化过程导致精度损失,可以获得更准确的状态估计效果。
5 参考文献
[1] Simo Srkk. Bayesian Filtering and Smoothing.
原创性声明:本文属于作者原创性文章,小弟码字辛苦,转载还请注明出处。谢谢~
如果有哪些地方表述的不够得体和清晰,有存在的任何问题,亦或者程序存在任何考虑不周和漏洞,欢迎评论和指正,谢谢各路大佬。
有需要相关技术支持的可咨询QQ:297461921