梯度下降的一个简单应用实例:三次函数拟合散点
1.基本原理:
使用梯度下降法使用三次函数模型去拟合散点,基本过程是:
- 根据三次函数模型给出损失函数
- 求偏导得到所有迭代式
- 编程实现
- 初始化自变量
- 设定学习速率 α
- 设置精度
- 运行程序得到结果
首先设定用来拟合的三元函数模型为:
y = h ( x ) = k 3 x 3 + k 2 x 2 + k 1 x + k 0 y=h(x)=k_{3}x^{3}+k_{2}x^{2}+k_{1}x+k_{0} y=h(x)=k3x3+k2x2+k1x+k0
然后给出在训练集上的损失函数:
J ( k 3 , k 2 , k 1 , k 0 ) = 1 2 m ∑ i = 1 m [ h ( x i ) − y i ] 2 J(k_{3},k_{2},k_{1},k_{0})=\frac{1}{2m}\sum_{i=1}^m[h(x_{i})-y_{i}]^{2} J(k3,k2,k1,k0)=2m1∑i=1m[h(xi)−yi]2
m 为训练集中的数据个数
为了编程实现,将 h ( x ) h(x) h(x)带入损失函数展开得:
J ( k 3 , k 2 , k 1 , k 0 ) = 1 2 m ∑ i = 1 m [ k 3 x 3 + k 2 x 2 + k 1 x + k 0 − y i ] 2 J(k_{3},k_{2},k_{1},k_{0})=\frac{1}{2m}\sum_{i=1}^m[k_{3}x^{3}+k_{2}x^{2}+k_{1}x+k_{0}-y_{i}]^{2} J(k3,k2,k1,k0)=2m1∑i=1m[k3x3+k2x2+k1x+k0−yi]2
接下来求出到编程中需要使用的迭代式:
-
要使用梯度下降算法对损失函数 J ( k 3 , k 2 , k 1 , k 0 ) J(k_{3},k_{2},k_{1},k_{0}) J(k3,k2,k1,k0) 进行最小化,就要分别对 k 3 k 2 k 1 k 0 k_{3} k_{2} k_{1} k_{0} k3k2k1k0进行求偏导。
-
梯度下降的原理式:
-
k i = k i − α ∂ J ( k 3 , k 2 , k 1 , k 0 ) ∂ k i k_{i}=k_{i}-\alpha\frac{\partial J(k_{3},k_{2},k_{1},k_{0})}{\partial k_{i}} ki=ki−α∂ki∂J(k3,k2,k1,k0)
-
-
结合损失函数 J ( k 3 , k 2 , k 1 , k 0 ) J(k_{3},k_{2},k_{1},k_{0}) J(k3,k2,k1,k0)和梯度下降原理式,得到迭代式:
k 3 = k 3 − α m ∑ i = 1 m ( k 3 x i 3 + k 2 x i 2 + k 1 x i + k 0 − y i ) x i 3 k 2 = k 2 − α m ∑ i = 1 m ( k 3 x i 3 + k 2 x i 2 + k 1 x i + k 0 − y i ) x i 2 k 1 = k 1 − α m ∑ i = 1 m ( k 3 x i 3 + k 2 x i 2 + k 1 x i + k 0 − y i ) x i k 0 = k 0 − α m ∑ i = 1 m ( k 3 x i 3 + k 2 x i 2 + k 1 x i + k 0 − y i ) k3=k3-\frac{\alpha}{m}\sum_{i=1}^{m}(k_{3}x_{i}^{3}+k_{2}x_{i}^{2}+k_{1}x_{i}+k_{0}-y_{i})x_{i}^{3} \\ k2=k2-\frac{\alpha}{m}\sum_{i=1}^{m}(k_{3}x_{i}^{3}+k_{2}x_{i}^{2}+k_{1}x_{i}+k_{0}-y_{i})x_{i}^{2} \\ k1=k1-\frac{\alpha}{m}\sum_{i=1}^{m}(k_{3}x_{i}^{3}+k_{2}x_{i}^{2}+k_{1}x_{i}+k_{0}-y_{i})x_{i}^{} \\ k0=k0-\frac{\alpha}{m}\sum_{i=1}^{m}(k_{3}x_{i}^{3}+k_{2}x_{i}^{2}+k_{1}x_{i}+k_{0}-y_{i}) k3=k3−mαi=1∑m(k3xi3+k2xi2+k1xi+k0−yi)xi3k2=k2−mαi=1∑m(k3xi3+k2xi2+k1xi+k0−yi)xi2k1=k1−mαi=1∑m(k3xi3+k2xi2+k1xi+k0−yi)xik0=k0−mαi=1∑m(k3xi3+k2xi2+k1xi+k0−yi)
2.代码实现:
(完整代码在最后)
在拟合之前,首先要初始化学习速率 α \alpha α 和 k 3 , k 2 , k 1 , k 0 k_{3},k_{2},k_{1},k_{0} k3,k2,k1,k0 (代码中使用的是 x 3 , x 2 , x 1 , x 0 ) x_{3},x_{2},x_{1},x_{0}) x3,x2,x1,x0)
- 对于学习速率 α \alpha α :
- 如果发现迭代过程发散了(溢出),则可以适当调小然后观察
- 如果发现迭代过程太慢(可以把中间迭代数据间隔性地输出),则可以调大一点(调整过度会有发散风险)
double alpha = 0.0000000000000008;
x3 = 0;
x2 = 0;
x1 = 0;
x0 = 0;
然后是迭代部分:
根据原理部分的迭代式进行计算和更新,直到全部满足一定的精度后停止迭代,得到拟合结果。
相关代码:
//首先计算和式
for(int i = 0;i < m;i++){
sum0 += (x3 * pow(x[i], 3) + x2 * pow(x[i], 2) + x1 * x[i] + x0 - y[i]);
sum1 += (x3 * pow(x[i], 3) + x2 * pow(x[i], 2) + x1 * x[i] + x0 - y[i]) * x[i];
sum2 += (x3 * pow(x[i], 3) + x2 * pow(x[i], 2) + x1 * x[i] + x0 - y[i]) * pow(x[i], 2);
sum3 += (x3 * pow(x[i], 3) + x2 * pow(x[i], 2) + x1 * x[i] + x0 - y[i]) * pow(x[i], 3);
}
//按照迭代公式进行迭代,这里要注意要保持k1234同时更新,如果提前更新了k1便会影响到k234的计算
temp0 = x0 - (alpha / m) * sum0;
temp1 = x1 - (alpha / m) * sum1;
temp2 = x2 - (alpha / m) * sum2;
temp3 = x3 - (alpha / m) * sum3;
//满足一定的精度后停止迭代
if((fabs(temp0-x0)<0.00000001) && (fabs(temp1-x1)<0.00000001)
&& (fabs(temp2-x2)<0.00000001) && (fabs(temp3-x3)<0.00000001)){
break;
}
//将迭代更新
x0 = temp0;
x1 = temp1;
x2 = temp2;
x3 = temp3;
3.结果分析:
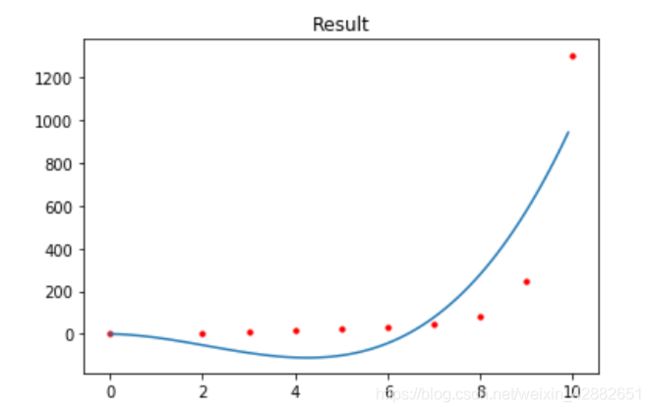
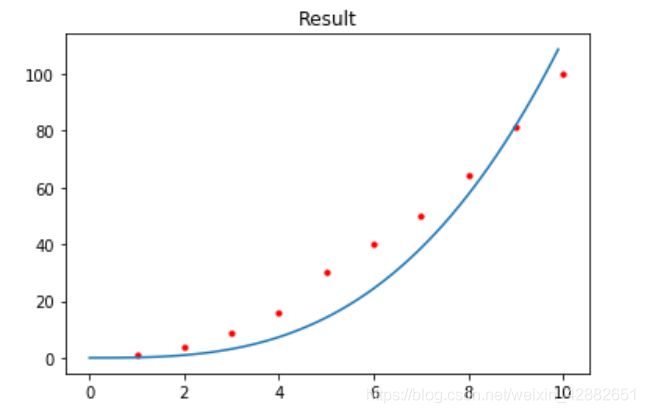
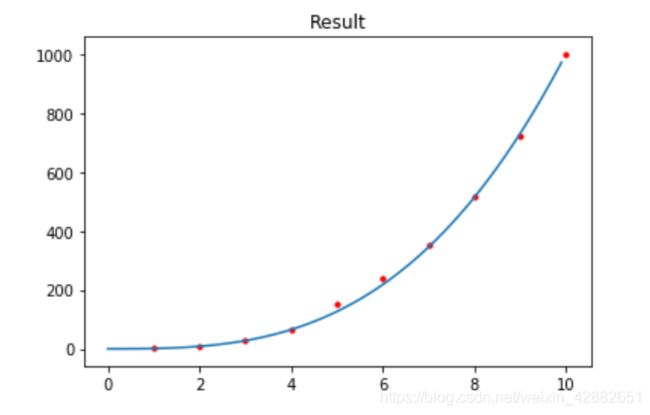
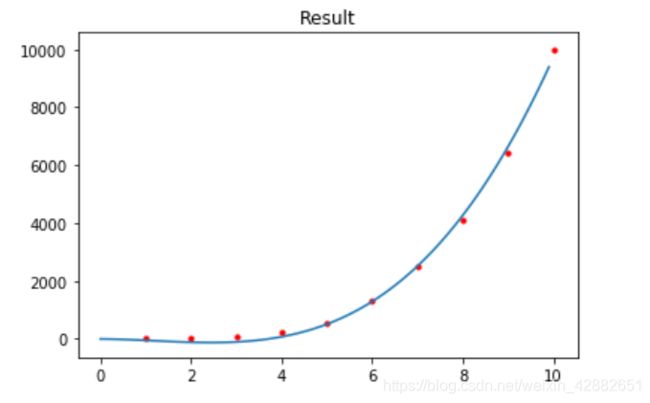
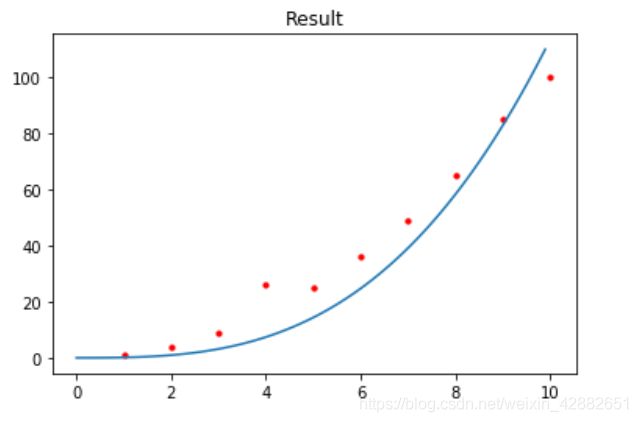
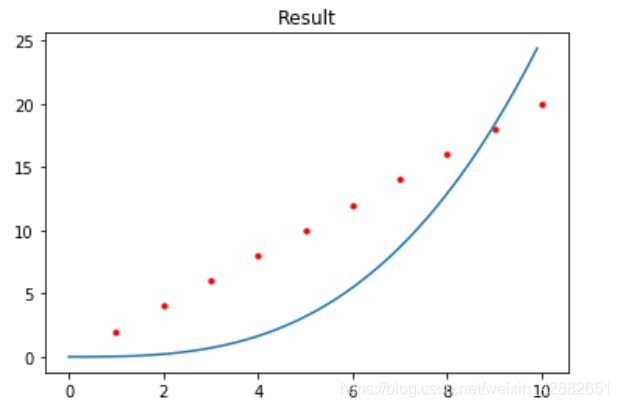
以下是几组数据拟合的情况,红色点为训练集,蓝色曲线为拟合结果
(为了绘图方便,仅从训练集中间隔选取一部分数据画出来)
训练集数据量的分析:
这里的拟合目标是 1 2 x 3 + 2 x 2 + x + 1 \frac{1}{2}x^{3}+2x^{2}+x+1 21x3+2x2+x+1
/*多组结果数据
各组学习速率 alpha 不同,所以循环次数的比较无意义
*/
数据量 10 循环 649669 次 结果 : y = 0.726796x^3+0.0862042x^2+0.0107911x+0.00147778
数据量 30 循环 9402416 次 结果 : y = 0.498747x^3+2.0656x^2+0.205435x+0.0173887
数据量 90 循环 3168008 次 结果 : y = 0.49982x^3+2.02649x^2+0.067502x+0.00188925
数据量 100 循环 1237039 次 结果 : y = 0.499818x^3+2.02702x^2+0.0608376x+0.00153463
数据量 170 循环 2616705 次 结果 : y = 0.499958x^3+2.01298x^2+0.035513x+0.000524415
数据量 250 循环 4922034 次 结果 : y = 0.500009x^3+2.00268x^2+0.0240199x+0.000240722
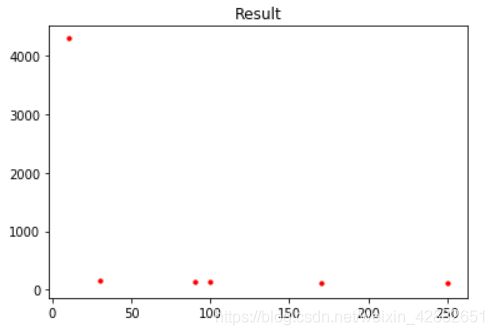
计算对应的加权误差: 加权误差 数据量
0.00147778 0.0107911 0.0862042 0.726796 4290.661912 10
0.0173887 0.205435 2.0656 0.498747 167.412613 30
0.00188925 0.06750 2.02649 0.49982 131.521108 90
0.00153463 0.0608376 2.02702 0.499818 132.740894 100
0.000524415 0.035513 2.01298 0.499958 119.843456 170
0.000240722 0.0240199 2.00268 0.500009 110.365603 250
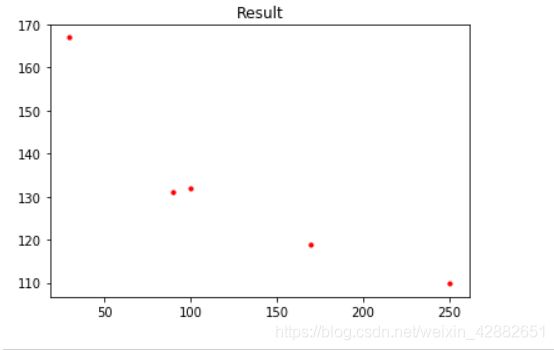
显然,随着数据量增大,加权误差总体上来说是在减小的。
但是还能得到一些结论:
-
对于一次和余数项的拟合,随着训练集的增大,拟合的情况反而更差。
-
数据量增大时,只有高次项(三次项和二次项)越来越准确。
有关拟合效果的分析:
对于类似三元函数的散点集,拟合的效果不错,但是对于其他的情形,拟合效果只能说是差强人意。
原因考虑到可能有以下两种情况,但是由于才学疏浅目前还不太明白
- 梯度下降时结束位于局部最优附近?
- 三次函数本身局限?
完整的代码:
#include
if(count % 100000 == 0){
cout<<count<< "结果 : y = "<<x3<<"x^3+"<<x2<<"x^2+"<<x1<<"x+"<<x0<<endl;
}
}
cout << "循环 " << count << " 次" << endl;
cout << "结果 : y = "<<x3<<"x^3+"<<x2<<"x^2+"<<x1<<"x+"<<x0<<endl;
}