Splay/伸展树(P3369 P3391 P2042)
什么是splay?
一种平衡二叉树。
什么是平衡二叉树?
需要先了解什么是:
二叉搜索树——简称BST,每个节点最多有两个子节点,左子比当前节点小,右子比当前节点大。
因此对于插入和查找第k小的值,都可以从根递归着进行下去,在到达递归终点之前,不是选择这个节点左儿子就是右儿子,因此,操作的复杂度 = 树的深度。
然而,这棵树的形状会因为你插入数字的顺序和大小不同,导致层数过大。比如你插入 1 2 3 4 5 6 7按照前面所说,形成的树就是七层了(也就是最坏情况--退化成链状),而你修改一下这七个数插入的顺序,形成的树的形状都和当前这个不同。
这棵树的形状也太随缘了吧,这可怎么办?
平衡二叉树(以下简称平衡树)就是利用各种手段,在不改变中序遍历的情况下搞这个BST的形状,使得BST趋向于平衡,也就是层数变少。
中序遍历:不同于前序遍历先遍历左儿子右儿子再是自己。中序遍历是先左儿子再自己再右儿子。
通过中序遍历,我们可以按照从小到大的顺序获得这棵BST上的值。
各种平衡树,如treap,AVL,红黑树,SBT,splay等,都是在不改变BST中序遍历结果的情况下改变树的结构。
而中序遍历不变,那么这两颗BST是等价的:因为新的树仍然拥有原树的所有数据,并且中序遍历结果不变,意味着仍旧符合BST的性质。
换种好理解的方式来说明的话:我们说1234567这种方式的插入是形成的BST最差的,各种平衡树的平衡操作,本质上就是不改变插入的是1234567这七个数,而是通过对BST的摆弄,相当于做了改变插入顺序形成形状更好的树(注意我只是说相当于),比如说4213657这个顺序插入形成的树就非常nice。
Splay如何平衡?
Splay平衡的操作就叫做splay(伸展),这个操作基于一种叫rotate(旋转)的操作。
rotate(其实是很多平衡树的基础操作)
旋转分为左旋和右旋。
左旋就是把左儿子转到父亲的位置,让父亲变为自己的右儿子,并让左儿子的右儿子成为父亲的左儿子。
右旋就是把右儿子转到父亲的位置,让父亲变为自己的左儿子,并让右儿子的左儿子成为父亲的右儿子。
如图
代码
const int N = 1e5+5;
int fa[N];//父亲是哪个节点
int ch[N][2];//数组第二维0,1分别表示左右儿子
void rotate(int x){ //x为将要旋转到父亲的节点,此函数能调用的条件是x有父亲
int f = fa[x]; //x的父亲(虽然快要给x当儿子了)
int d = ch[f][0] == x? 1:0; //判断是需要左旋还是右旋,d = 1表示右旋,d = 0表示左旋
fa[x] = fa[f],fa[f] = x,fa[ch[x][d]] = f; //正确维护旋转后的fa数组
ch[x][d] = f,ch[f][d^1] = ch[x][d]; //改变父子关系,d^1等价于:1变0,0变1
if (fa[x]) ch[fa[x]][ch[fa[x]]==f?0:1] = x;//原本f有父亲的话,现在需要连向x,第二维里面的那个式子是在判断f原先是其父亲的左儿子还是右儿子
push_up(f),push_up(x); //像线段树一样push_up以正确维护当前节点的信息,注意顺序!!!要先f再x
}splay
splay其实就是不停的rotate。
splay需要传入两个参数x,goal,第一个就是需要splay的节点,第二个就是x需要不停向上转向上转,直到转到以goal为父节点。
(x:我往上转往上转,我一定要做goal的儿子啊啊啊啊啊)
当然具体没那么简单。
定义f为x的父亲、g为f的父亲,也就是x的爷爷。
我们现在要把x转到g,需要转两次,这里怎么转就有讲究了。
不会证明但是可以把BST搞平衡的旋转方法:
如果x,f,g三点一线,那么先旋转f,再旋转x
否则旋转两次x
反正...这么旋转就能平衡,每次插入一个数之后马上splay这个点到根节点这棵树就平衡了。啥均摊logN的咱也不懂,感兴趣的可以去看看证明。
代码
void splay(int x,int goal=0){//第二个蚕食不传入默认为0,只有fa[root] = 0,因此默认splay到根节点
while (fa[x] != goal){
int f = fa[x],g = fa[f];
if (g!=goal) rotate((ch[f][0]==x)==(ch[g][0]==f)? f:x);//g==goal表示转一次父亲就是goal了,这个if就不用进了
rotate(x); //然后上面的if里面就是在判断祖孙仨儿是不是三点一线
}
if (!goal) root = x;//此时修改根节点
}以上就是基本平衡的操作,具体怎么实现插入删除查找通过下面的题来学!
>>>洛谷3369
6种操作:
①插入一个数
②删除一个数
③查x的排名
④查排名为x
⑤求x的前驱(比x小的最大的数)
⑥求x的后继(比x大的最小的数)
咱也分六部分讲吧,先给出开了那些数组和基本的函数,最难是删除,咱放最后讲。
int ch[N][2];//两个儿子
int fa[N];//父亲
int size[N];//子树大小(节点数)
int cnt[N];//该点的值出现了几次(插入了几个),题目明确说没有插入重复数字就可以不用这个数组,不过其实就算有也可以不用
int val[N];//节点的值
int sz,root;//sz是下一个新建节点的下标,root是根
void init(){
sz = 1;
root = 0;
}
int newnode(int v,int f){//v,f是将要新建节点的值,父亲
ch[sz][0] = ch[sz][1] = 0;
fa[sz] = f;
size[sz] = cnt[sz] = 1;
val[sz] = v;
return sz++;//返回新节点下标,并自增1
}
void push_up(int rt){
size[rt] = cnt[rt] + size[ch[rt][0]] + size[ch[rt][1]];
}
void rotate(int x){
int f = fa[x];
int d = ch[f][0]==x? 1:0;
fa[x] = fa[f],fa[f] = x,fa[ch[x][d]] = f;
ch[f][d^1] = ch[x][d];
ch[x][d] = f;
if (fa[x]) ch[fa[x]][ch[fa[x]][0]==f?0:1] = x;
push_up(f);push_up(x);
}
void splay(int x,int goal=0){
while (fa[x] != goal){
int f = fa[x],g = fa[f];
if (g!=goal) rotate((ch[f][0]==x)==(ch[g][0]==f)? f:x);
rotate(x);
}
if (!goal) root = x;
}插入
其实在讲splay的时候我们讲过了。
就找到合适的位置然后让父亲链上他,然后splay这个点到根就可以让树平衡了。
void insert(int v){
int now = root,f=0;//f记录新建节点的父亲,一定要初始化为0
while (now && val[now]!=v) f = now,now = ch[now][v>val[now]];
if (now) cnt[now]++;//这个节点已经有了就不用新建,直接次数+1
else {now = newnode(v,f);if (f)ch[f][v>val[f]] = now;}//newnode用于新建一个节点,然后一定要连到树上啊
splay(now);//通过splay重构了一下树,并(主要是)正确更新了原本由于新插入一个节点而产生错误的祖先节点的信息
}查x的排名
也就是一直深搜下去把左子树的size一直累积直到当前节点的值就是v,注意看那行注释
int rank(int v){
int now = root,ans = 0;
while (now){
if (val[now]>v) now = ch[now][0];
else{
ans += size[ch[now][0]];
if (val[now]==v) {splay(now);return ans+1;}//此处需要splay的原因是为了方便求前驱后继,否则可以不要
ans += cnt[now];
now = ch[now][1];
}
}
}找排名为x的数
int kth(int k){
int now = root;
while (now){
if (k<=size[ch[now][0]]) now = ch[now][0];//k在左子树
else {
k -= size[ch[now][0]] + cnt[now];//k不在左子树,那么减去左子树的子树大小和当前节点的大小
if (k<=0) return val[now];//表明在当前节点
else now = ch[now][1];//否则在右子树找此时的第k大
}
}
}前驱后继
直接逼近就可以了,因为其他地方有需要所以还要同时记录一下节点是哪个
int getpre(int v,bool getid=false){//getid = true就返回前驱的下标
int ans = -INF,id = 0;
int now = root;
while (now){
if (val[now]>=v) now = ch[now][0];
else{
if (val[now]>ans) ans = val[now],id = now;
now = ch[now][1];
}
}
return getid?id:ans;
}
int getsuc(int v,bool getid=false){
int ans = INF,id = 0;
int now = root;
while (now){
if (val[now]<=v) now = ch[now][1];
else {
if (val[now]删除
首先我们找到v所在的节点并把它搞到根,然后分类讨论。
①如果这个节点的cnt>1那么好办了,直接cnt--即可
②只有一个节点,那么也好办,直接root = 0
③如果只有左子树或者右子树,那么就让root = 存在的那个儿子即可,也很方便,但是注意要fa[root],不然下次这个点要splay的时候,emm,会把删掉的点重新搞出来,因为此时fa[root]不等于0,x还在往上转!
④左右儿子都有,那么找到前驱,再把前驱翻到根,此时右儿子就是原本v所在的节点。此时是下图的状态,只要让前驱连到根的右儿子即可。这里很值得细细说一说。
splay前驱之前,前驱一定在root的左子树,我们要知道,之前我们说过,splay过程,三点一线要先转父亲,此时根节点是有可能会先被转下去的!然而当前则是特殊情况,此时绝不会形成根 - 某某 - 前驱这样三点一线的情况,因为前驱就是root左子树比root小的最大数。
代码
void remove(int v){
rank(v);//找到值为v的点并splay到根
if (cnt[root]>1) cnt[root]--;
else if (!ch[root][0] && !ch[root][1]) root = 0;
else if (!ch[root][0] || !ch[root][1]) root = ch[root][0]?ch[root][0]:ch[root][1],fa[root] = 0;//fa[root] = 0很关键,不然这个点旋转时会重新搞出删掉的节点
else {
int p = getpre(v,true);//保证有前驱后继,因为左右子树都有才能进这个else
int old = root;
splay(p);//这里知道点在哪儿,直接splay ,前驱直接splay到根的话,根一定在右儿子(不会三点一线,消失不见)
fa[ch[old][1]] = p;
ch[p][1] = ch[old][1];
push_up(p);
}
}OK,然后是整体的代码
#include
using namespace std;
#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;ival[now]];//第一遍说:这里是大于
if (now) cnt[now]++;
else {now = newnode(v,f);if (f)ch[f][v>val[f]] = now;}
splay(now);//通过splay重构了一下树,并(主要是)正确更新了原本由于新插入一个节点而产生错误的祖先节点的信息
}
void remove(int v){
rank(v);//找点并splay,因为还不知道v在哪,不知道从哪splay
if (cnt[root]>1) cnt[root]--;
else if (!ch[root][0] && !ch[root][1]) root = 0;
else if (!ch[root][0] || !ch[root][1]) root = ch[root][0]?ch[root][0]:ch[root][1],fa[root] = 0;//fa[root] = 0很关键,不然这个点旋转时会重新搞出删掉的节点
else {
int p = getpre(v,true);//保证有前驱后继,因为左右子树都有才能进这个else
int old = root;
splay(p);//这里知道点在哪儿,直接splay ,前驱直接splay到根的话,根一定在右儿子(不会三点一线,消失不见)
fa[ch[old][1]] = p;
ch[p][1] = ch[old][1];
push_up(p);
}
}
int rank(int v){
int now = root,ans = 0;
while (now){
if (val[now]>v) now = ch[now][0];
else{
ans += size[ch[now][0]];
if (val[now]==v) {splay(now);return ans+1;}//此处需要splay的原因与求前驱后继有关
ans += cnt[now];
now = ch[now][1];
}
}
}
int kth(int k){
int now = root;
while (now){
if (k<=size[ch[now][0]]) now = ch[now][0];
else {
k -= size[ch[now][0]] + cnt[now];
if (k<=0) return val[now];
else now = ch[now][1];
}
}
}
int getpre(int v,bool getid=false){//getid = true就返回前驱的下标
int ans = -INF,id = 0;
int now = root;
while (now){
if (val[now]>=v) now = ch[now][0];
else{
if (val[now]>ans) ans = val[now],id = now;
now = ch[now][1];
}
}
return getid?id:ans;
}
int getsuc(int v,bool getid=false){
int ans = INF,id = 0;
int now = root;
while (now){
if (val[now]<=v) now = ch[now][1];
else {
if (val[now] >>>洛谷3391
本题是将区间操作:区间翻转
类似线段树,打个标记区间修改,然后配合push_down函数使用。
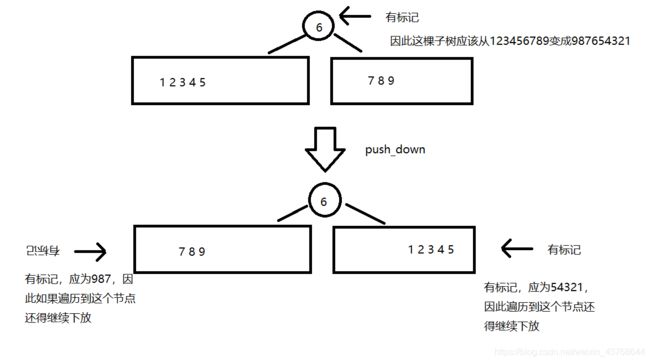
问题是我们需要修改的区间不在一个一颗子树我们怎么打标记?
因此需要一波操作,重构一下平衡树,把询问的区间整合到一棵子树上直接给那棵子树打标记,也就是提取这一段区间。
具体可以这样实现:
假定询问区间是[l,r],我们找到第l-1个节点(找排名第几的点这个操作上面那题实现过了),把它splay到根,
再找到第r+1个点,splay到根的右儿子,此时,我们看图
如图,根的右儿子的左儿子就是我们要的子树。
然后打个标记。
之后每次遍历到这个点的时候下放一下,具体就是交换一下左右子树,并且左右子树标记翻新一下,然后去掉自己的标记。
看图
因为左子树原本都在当前节点左边,右子树都在右边,翻转之后必然左子树都在右边,右子树都在左边,而这两棵子树都要再各自翻转,这个任务就交给两个儿子自己办啦。
剩下的一些事情:
①我们说明一下splay过程正确性,之前我们不是splayl-1,r+1了吗,这个过程从底到顶,不是完全会和标记维护下的树产生冲突吗?
不会,因为我们调用kth找到这个点的时候也会下放。
因此splay上去过程遇到的都是之前kth逐层找下来的点,它们都被下放过。
②提取区间方法不止上面的一种,但是千万不要这样:
r+1splay到根,再l-1splay到根,受上面那题影响,以为l-1翻到根节点以后r+1一定是右儿子,然而并不一定,因为可能会三点一线,然后r+1就被翻下去了。
③建树
不用像上一题一样这么插入啦,因为现在不是随机按值插入,现在就相当于谁的下标大,谁就大,维护的只是中序遍历下的一个顺序而已,那我们肯定可以自己建一棵层数logn的树啦,只要类似线段树build函数一样,根据中序遍历的顺序给节点赋值就可以了,具体参考本题完整代码中的build函数,这样复杂度也是O(N),因为线段树也是O(N)的。
④整颗子树原先有标记再被打了一次标记相当于整棵子树不用转了。
⑤提取区间的时候我分了一下类,先判断掉了特殊情况,网上也有其他办法,好像是加两个赋值节点,具体看代码
代码
#include
using namespace std;
#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;ir) return ;
if (l==r){
rt = newnode(l,f);
return ;
}
int mid = l+r>>1;
rt = newnode(mid,f);
build(ch[rt][0],l,mid-1,rt);
build(ch[rt][1],mid+1,r,rt);
push_up(rt);
}
void reverse(int l,int r){
int sl,sr;
if (l==1 && r==n) rev[root] ^= 1;
else if (l==1) sr = kth(root,r+1),splay(sr),rev[ch[root][0]] ^= 1;
else if (r==n) sl = kth(root,l-1),splay(sl),rev[ch[root][1]] ^= 1;
else {
sl = kth(root,l-1);
splay(sl);//get_tree(root);
sr = kth(root,r+1);
//pt(ch[root][1]);
splay(sr,root);//get_tree(root);
//pt(sl);
//pt(sr);
//DFS(ch[ch[root][1]][0]);
rev[ch[ch[root][1]][0]] ^= 1;
}
}
int kth(int rt,int k){
push_down(rt);
if (k<=size[ch[rt][0]]) return kth(ch[rt][0],k);
k -= size[ch[rt][0]] + cnt[rt];
if (k<=0) return rt;
else return kth(ch[rt][1],k);
}
/*输出与debug函数*/
int flag;
void DFS(int rt){
flag = true;
dfs(rt);
puts("");
}
void dfs(int now){
push_down(now);
if (ch[now][0]) dfs(ch[now][0]);
flag? flag = false:printf(" ");
//printf("val[%d]=%d",now,val[now]);
printf("%d",val[now]);
if (ch[now][1]) dfs(ch[now][1]);
}
/*
void get_tree(int rt){
printf("%d : %d %d\n",rt,ch[rt][0],ch[rt][1]);
if (ch[rt][0]) get_tree(ch[rt][0]);
if (ch[rt][1]) get_tree(ch[rt][1]);
}
*/
}sp;
int main()
{
int q;
scanf("%d %d",&n,&q);
int l,r;
sp.init();
sp.build(sp.root,1,n,0);
//sp.DFS(sp.root);
while (q--){
scanf("%d %d",&l,&r);
sp.reverse(l,r);
//sp.DFS(sp.root);
}
sp.DFS(sp.root);
return 0;
}
>>>洛谷2042
这题就比较硬核了。
不过有了上题的基础应该...也做不出来。
先讲最难的
求和区间最大的子列
所以先做一下这题或者理解一下这题的思路>>>Vijos1083
然后你就大概知到这三行代码什么意思了。
l[rt] = max(l[lson],sum[lson]+l[rson]);
r[rt] = max(r[rson],sum[rson]+r[lson]);
mcs[rt] = max(max(mcs[lson],mcs[rson]),r[lson]+l[rson]);l,r表示区间从左,右端点开始的最大连续和,至少得取第一位。
比如-1 -1 -1 -1 -1,l和r都是-1
mcs表示区间最大连续和,lson,rson表示左右儿子
对比线段树中的写法
上面是线段树的写法,平衡树中就这样:
l[rt] = max(max(l[ch[rt][0]],sum[ch[rt][0]]+val[rt]),sum[ch[rt][0]]+val[rt]+l[ch[rt][1]]);
r[rt] = max(max(r[ch[rt][1]],sum[ch[rt][1]]+val[rt]),sum[ch[rt][1]]+val[rt]+r[ch[rt][0]]);
mcs[rt] = max(max(mcs[ch[rt][0]],mcs[ch[rt][1]]),max(0,r[ch[rt][0]])+val[rt]+max(0,l[ch[rt][1]]));我们需要将0节点的l,r,mcs初始化为-INF,为什么呢,因为不同于线段树每个节点一旦有儿子就有两个,平衡树中可能只有一个儿子,没有左右儿子(即指向0节点),根据l,r,mcs的定义,现在那个儿子没有,当前对应的l,r就没有,那么就是-INF
对于第三个式子,由于l,r可以不选,所以还需要和0比较取较大的。
然后按顺序讲一下其他操作:
插入
用上一题方式建树,然后用上一题方式提取[pos,pos+tot-1]区间,然后把这棵树插进平衡树,push_up一下对应的节点
删除
提取区间,整棵树去掉。
这里需要回收删掉的节点。因为我们开不起数据规模400w的平衡树,只能开50w的,所以我们手动模拟一个队列space,用掉了就弹出,回收了就进入,删除具体看代码中del()函数,很简单的。
修改
提取区间,打标记,上面区间翻转都会,这个应该更简单吧。
一个技巧:下放的时候如果该点有修改标记,可以修改完之后把该点的翻转标记去掉,因为子树内数都一样,就不用翻转了。
翻转
你会了,需注意的是每次打标记,对,是打标记不是下放标记,的时候交换一下l,r,对,不是交换左右儿子,这样才能保持当前节点l,r正确
求和
该push_up的地方push_up就行
其他还有什么细节想不到了...
对了想起来了,区间修改的懒惰标记记得只用0,1表示是否有标记,不要表示整颗子树需要修改的值,因为可能区间修改的值就是0.很关键。
对了,这题想看无旋treap版本的题解也可以看我另一篇博客>>>无旋treap做法
代码(加了个快读模板和一些没用的函数之后代码有点长)
#include
using namespace std;
#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;i ' '; l++) s[cur++] = buf[l];
if (l < r) break;
l = 0, r = int(fread(buf, 1, SIZE, stdin));
}
s[cur] = '\0';
return cur;
}
template
bool read(type &x, int len = 0, int cur = 0, bool flag = false) {
if (!(len = read(str))) return false;
if (str[cur] == '-') flag = true, cur++;
for (x = 0; cur < len; cur++) x = x * 10 + str[cur] - '0';
if (flag) x = -x;
return true;
}
template
type read(int len = 0, int cur = 0, bool flag = false, type x = 0) {
if (!(len = read(str))) return false;
if (str[cur] == '-') flag = true, cur++;
for (x = 0; cur < len; cur++) x = x * 10 + str[cur] - '0';
return flag ? -x : x;
}
} using FastI::read;
const int N = 5e5+10;
struct SPLAY{
int ch[N][2];
int fa[N];
int val[N];
int size[N];
int l[N],r[N],mcs[N];
int rev[N];
int tag[N];
int sum[N];
int root;
int space[N],st,ed;
int cnt;//节点个数
int a[N];//用于输入数据
void init(){
root = cnt = 0;
l[0] = r[0] = mcs[0] = -INF;
for1(i,1,500005) space[i] = i;
st = 1,ed = 1;
}
int newnode(int v,int f){
int sz = space[st++];if (st==500006) st = 1;
fa[sz] = f;
ch[sz][0] = ch[sz][1] = 0;
val[sz] = l[sz] = r[sz] = mcs[sz] = sum[sz] = v;
size[sz] = 1;
rev[sz] = tag[sz] = 0;
return sz;
}
void use_to_reverse(int rt){
if (!rt) return ;
swap(l[rt],r[rt]);
rev[rt] ^= 1;
}
void use_to_update(int rt,int v){
if (!rt) return ;
tag[rt] = 1;
val[rt] = v;
sum[rt] = v*size[rt];
l[rt] = r[rt] = mcs[rt] = max(v,sum[rt]);
}
void push_up(int rt){
size[rt] = size[lson] + size[rson] + 1;
sum[rt] = sum[lson] + val[rt] + sum[rson];
l[rt] = max(max(l[ch[rt][0]],sum[ch[rt][0]]+val[rt]),sum[ch[rt][0]]+val[rt]+l[ch[rt][1]]);
r[rt] = max(max(r[ch[rt][1]],sum[ch[rt][1]]+val[rt]),sum[ch[rt][1]]+val[rt]+r[ch[rt][0]]);
mcs[rt] = max(max(mcs[ch[rt][0]],mcs[ch[rt][1]]),max(0,r[ch[rt][0]])+val[rt]+max(0,l[ch[rt][1]]));
}
void push_down(int rt){
if (!rt) return ;
if (tag[rt]){
if (lson) use_to_update(lson,val[rt]);
if (rson) use_to_update(rson,val[rt]);
tag[rt] = 0;
rev[rt] = 0;
}
if (rev[rt]){
swap(lson,rson);
if (lson) use_to_reverse(lson);
if (rson) use_to_reverse(rson);
rev[rt] = 0;
}
}
void rotate(int x){
int f = fa[x];
int d = ch[f][0]==x? 1:0;
fa[x] = fa[f],fa[f] = x,fa[ch[x][d]] = f;
ch[f][d^1] = ch[x][d],ch[x][d] = f;
if (fa[x]) ch[fa[x]][ch[fa[x]][0]==f?0:1] = x;
push_up(f),push_up(x);
}
void splay(int x,int goal=0){
while (fa[x]!=goal){
int f = fa[x],g = fa[f];
if (g!=goal) rotate( (ch[f][0]==x) == (ch[g][0]==f)?f:x );
rotate(x);
}
if (!goal) root = x;
}
int kth(int rt,int k){
push_down(rt);
if (k<=size[lson]) return kth(lson,k);
k -= size[lson] + 1;
if (k<=0) return rt;
else return kth(rson,k);
}
void build(int& rt,int l,int r,int f){
if (l>r) return ;
if (l==r){
rt = newnode(a[l],f);
return ;
}
int mid = l+r>>1;
rt = newnode(a[mid],f);
build(lson,l,mid-1,rt);
build(rson,mid+1,r,rt);
push_up(rt);
}
void interval(int& node,int& d,int l,int r){///提取这一段区间
int ls,rs;
if (l==1 && r==cnt) node = root,d = -1;
else if (l==1) rs = kth(root,r+1),splay(rs),node = root,d = 0;
else if (r==cnt) ls = kth(root,l-1),splay(ls),node = root,d = 1;
else {
ls = kth(root,l-1),rs = kth(root,r+1);
splay(ls);
//printf("Line167,see the tree after splay(ls):\n");BUG();
splay(rs,root);
node = ch[root][1],d = 0;
}
}
void insert(int p,int tot){
for1(i,1,tot) read(a[i]);
int newroot;
build(newroot,1,tot,0);
int ls,rs;
if (p==0){
ls = kth(root,1),splay(ls);
ch[root][0] = newroot;
fa[newroot] = root;
push_up(root);
}
else if (p==cnt){
rs = kth(root,cnt),splay(rs);
ch[root][1] = newroot;
fa[newroot] = root;
push_up(root);
}
else {
ls = kth(root,p),rs = kth(root,p+1);
splay(ls),splay(rs,root);
ch[ch[root][1]][0] = newroot;
fa[newroot] = ch[root][1];
push_up(ch[root][1]);
push_up(root);
}
cnt += tot;
}
void remove(int p,int tot){
int node,d;
interval(node,d,p,p+tot-1);
if (d==-1){del(root);root = 0;return ;}
//printf("Line 205,show the tree and which node you delete:\n");BUG();printf("node=%d,d=%d ->%d\n",node,d,ch[node][d]);
del(ch[node][d]);
ch[node][d] = 0;
push_up(node);
if (fa[node])push_up(fa[node]);
cnt -= tot;
}
void reverse(int p,int tot){
int node,d;
interval(node,d,p,p+tot-1);
if (d==-1){use_to_reverse(root);return ;}
use_to_reverse(ch[node][d]);
push_up(node);
if (fa[node])push_up(fa[node]);
}
void update(int p,int tot,int v){
int node,d;
interval(node,d,p,p+tot-1);
if (d==-1){use_to_update(root,v);return ;}
use_to_update(ch[node][d],v);
push_up(node);
if (fa[node]) push_up(fa[node]);
}
int getsum(int p,int tot){
if(tot==0) return 0;
int node,d;
interval(node,d,p,p+tot-1);
if (d==-1) return sum[root];
//printf("Line236,which node use to getsum?node = %d,d = %d->%d\n",node,d,ch[node][d]);
return sum[ch[node][d]];
}
int getmcs(){
return mcs[root];
}
void del(int rt){
if (!rt) return ;
if (lson) del(lson);
if (rson) del(rson);
space[ed++] = rt;if (ed==500006) ed = 1;
}
/*debug部分*/
void DE(){dfs1(root);puts("");}
void dfs1(int rt){
push_down(rt);
if (lson) dfs1(lson);
//printf("%d ",val[rt]);
printf("val[%d]=%d,sum[%d]=%d\n",rt,val[rt],rt,sum[rt]);
if (rson) dfs1(rson);
}
void BUG(){dfs2(root);puts("");}
void dfs2(int rt){
push_down(rt);
printf("%d : ",rt);
lson?printf("%d ",lson):printf("No ");
rson?printf("%d\n",rson):printf("No\n");
if (lson) dfs2(lson);
if (rson) dfs2(rson);
}
}sp;
int main()
{
//freopen("C/Users/DELL/Desktop/input.txt", "r", stdin);
//freopen("C/Users/DELL/Desktop/output.txt", "w", stdout);
sp.init();
int n,m;
read(n);read(m);
for1(i,1,n) read(sp.a[i]);
sp.build(sp.root,1,n,0);
sp.cnt = n;
//sp.DE();sp.BUG();
char op[20];
int p,tot,v;
while (m--){
read(op);
if (op[2]=='S') read(p),read(tot),sp.insert(p,tot);
if (op[2]=='L') read(p),read(tot),sp.remove(p,tot);
if (op[2]=='K') read(p),read(tot),read(v),sp.update(p,tot,v);
if (op[2]=='V') read(p),read(tot),sp.reverse(p,tot);
if (op[2]=='T') read(p),read(tot),printf("%d\n",sp.getsum(p,tot));
if (op[2]=='X') printf("%d\n",sp.getmcs());
//printf("Line291,after this option:\n");sp.DE();sp.BUG();
}
return 0;
}
后续还有啥必须splay写的好题就继续更咕咕咕.