1.3 向量方程(线性代数及其应用-第5版-系列笔记)
内容概述
本节首先以 R 2 \mathbb{R}^2 R2和 R 3 \mathbb{R}^3 R3空间为例,引入了向量的概念、向量的几何表示,并介绍了向量的一些基本运算和性质,例如向量的加法和标量乘法、交换律、结合律等。接着引入了线性组合的概念,并将线性组合和线性方程组结合了起来。
R 2 \mathbb{R}^2 R2中的向量
仅含一列的矩阵称为列向量,或简称向量。举例如下:
u = [ 1 2 ] \boldsymbol u = \begin{bmatrix}1 \\2 \end{bmatrix} u=[12], v = [ 0.2 0.3 ] \boldsymbol v = \begin{bmatrix}0.2 \\0.3 \end{bmatrix} v=[0.20.3]
所有两个元素的向量的集记为 R 2 \mathbb{R}^2 R2, R \mathbb{R} R表示向量中的元素是实数,而指数2表示每个向量包含两个元素。
R 2 \mathbb{R}^2 R2中两个向量相等当且仅当其对应元素相等,因为 R 2 \mathbb{R}^2 R2中的向量是实数的有序对。
给定 R 2 \mathbb{R}^2 R2中两个向量 u \boldsymbol u u和 v \boldsymbol v v,它们的和 u + v \boldsymbol u+\boldsymbol v u+v是把 u \boldsymbol u u和 v \boldsymbol v v对应元素相加所得的向量。例如, u = [ 1 2 ] \boldsymbol u = \begin{bmatrix}1\\ 2 \end{bmatrix} u=[12]和 v = [ 2 5 ] \boldsymbol v = \begin{bmatrix}2\\ 5 \end{bmatrix} v=[25]两个向量的和是 w = [ 3 7 ] \boldsymbol w = \begin{bmatrix}3\\ 7 \end{bmatrix} w=[37]
给定向量 u \boldsymbol u u和实数 c c c, u \boldsymbol u u与 c c c的标量乘法是把 u \boldsymbol u u的每个元素乘以 c c c,所得向量记为 c u c \boldsymbol u cu。
例如,
若
u = [ 3 − 1 ] , c = 5 \boldsymbol u=\begin{bmatrix} 3 \\ -1 \end{bmatrix}, \quad c = 5 u=[3−1],c=5
则
c u = 5 [ 3 − 1 ] = [ 15 − 5 ] c \boldsymbol u = 5\begin{bmatrix} 3 \\ -1 \end{bmatrix}=\begin{bmatrix} 15 \\ -5 \end{bmatrix} cu=5[3−1]=[15−5]
R 2 \mathbb{R}^2 R2的几何表示
因为平面上每个点由实数的有序对确定,所以可把集合点 ( a , b ) (a, b) (a,b)与列向量 [ a b ] \begin{bmatrix} \boldsymbol a \\ \boldsymbol b \end{bmatrix} [ab]等同。因此,可把 R 2 \mathbb{R}^2 R2看作平面上所有点的集合。
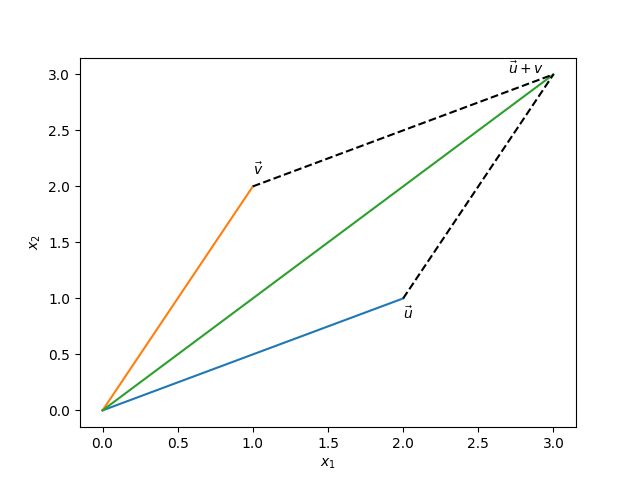
若 R 2 \mathbb{R}^2 R2中向量 u \boldsymbol u u和 v \boldsymbol v v用平面上的点表示,则 u + v \boldsymbol u + \boldsymbol v u+v对应于以 u \boldsymbol u u, 0 \boldsymbol 0 0和 v \boldsymbol v v为三个顶点的平行四边形的第4个顶点。
R 3 \mathbb{R}^3 R3中的向量
R 3 \mathbb{R}^3 R3中的向量是 3 × 1 3 \times 1 3×1列矩阵,有3个元素,它们表示三维坐标空间中的点,或起点为原点的箭头。

R n \mathbb{R}^n Rn中的向量
若 n n n是正整数,则 R n \mathbb{R}^n Rn表示所有 n n n个实数数列(或有序 n n n元组)的集合,通常写成 n × 1 n \times1 n×1列矩阵的形式,如:
u = [ u 1 u 2 . . . u n ] \boldsymbol u = \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix} u=⎣⎢⎢⎡u1u2...un⎦⎥⎥⎤
所有元素都是零的向量称为零向量,用 0 \boldsymbol 0 0表示( 0 \boldsymbol 0 0中元素的个数可由上下文确定。)
下列是 R n \mathbb{R}^n Rn中向量的代数性质:
u + v \boldsymbol u + \boldsymbol v u+v = v + u \boldsymbol v + \boldsymbol u v+u
( u + v ) + w = u + ( v + w ) (\boldsymbol u + \boldsymbol v) + \boldsymbol w = \boldsymbol u + (\boldsymbol v + \boldsymbol w) (u+v)+w=u+(v+w)
u + 0 = 0 + u = u \boldsymbol u + \boldsymbol 0 = \boldsymbol 0 + \boldsymbol u = \boldsymbol u u+0=0+u=u
u + ( − u ) = − u + u = 0 \boldsymbol u + (\boldsymbol {-u}) = -\boldsymbol u + \boldsymbol u = \boldsymbol 0 u+(−u)=−u+u=0
c ( u + v ) = c u + c v c(\boldsymbol u +\boldsymbol v) = c\boldsymbol u + c\boldsymbol v c(u+v)=cu+cv
( c + d ) u = c u + d u (c + d)\boldsymbol u = c\boldsymbol u + d\boldsymbol u (c+d)u=cu+du
c ( d u ) = ( c d ) u c(d\boldsymbol u) = (cd)\boldsymbol u c(du)=(cd)u
1 u = u 1\boldsymbol u = \boldsymbol u 1u=u
线性组合
给定 R n \mathbb{R}^n Rn中向量 v 1 , v 2 , ⋯ , v p \boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p v1,v2,⋯,vp和标量 c 1 , c 2 , ⋯ , c p c_1, c_2,\cdots, c_p c1,c2,⋯,cp,向量
y = c v 1 + ⋯ + c p v p \boldsymbol y=c\boldsymbol v_1 + \cdots +c_p\boldsymbol v_p y=cv1+⋯+cpvp
称为向量以 c 1 , c 2 , ⋯ , c p c_1, c_2,\cdots, c_p c1,c2,⋯,cp为权的线性组合。
从几何上来说,线性组合可以认为是不同向量拉伸和压缩之后的和。
下面的例子把线性组合与前面几节(1.1节、1.2节)的存在性问题联系起来。
设 a 1 = [ 1 − 2 − 5 ] \boldsymbol a_1 = \begin{bmatrix}1 \\ -2 \\ -5\end{bmatrix} a1=⎣⎡1−2−5⎦⎤, a 2 = [ 2 5 6 ] \boldsymbol a_2 = \begin{bmatrix}2 \\ 5 \\ 6\end{bmatrix} a2=⎣⎡256⎦⎤, b = [ 7 4 − 3 ] \boldsymbol b = \begin{bmatrix}7 \\ 4 \\ -3\end{bmatrix} b=⎣⎡74−3⎦⎤,确定 b \boldsymbol b b能否写成 a 1 \boldsymbol a_1 a1和 a 2 \boldsymbol a_2 a2的线性组合,也就是说,确定是否存在 x 1 x_1 x1和 x 2 x_2 x2,使得
x 1 a 1 + x 2 a 2 = b x_1\boldsymbol a_1 + x_2\boldsymbol a_2 = \boldsymbol b x1a1+x2a2=b
若该向量方程有解,求它的解。
解:该向量方程可以写为:
[ x 1 + 2 x 2 − 2 x 1 + 5 x 2 − 5 x 1 + 6 x 2 ] = [ 7 4 − 3 ] \begin{bmatrix}x_1 + 2x_2 \\-2x_1 + 5x_2 \\-5x_1 + 6x_2\end{bmatrix} = \begin{bmatrix}7\\4 \\-3\end{bmatrix} ⎣⎡x1+2x2−2x1+5x2−5x1+6x2⎦⎤=⎣⎡74−3⎦⎤
写成矩阵形式为:
[ 1 2 7 − 2 5 4 − 5 6 − 3 ] \begin{bmatrix} 1 & 2 & 7 \\ -2 & 5 & 4 \\ -5 & 6 & -3 \end{bmatrix} ⎣⎡1−2−525674−3⎦⎤
化为简化阶梯形为:
[ 1 0 3 0 1 2 0 0 0 ] \begin{bmatrix} 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{bmatrix} ⎣⎡100010320⎦⎤
其解是 x 1 = 3 , x 2 = 2 x_1 = 3, x_2 = 2 x1=3,x2=2,因此 b \boldsymbol b b是 a 1 \boldsymbol a_1 a1与 a 2 \boldsymbol a_2 a2的线性组合,权为: x 1 = 3 x_1=3 x1=3和 x 2 = 2 x_2=2 x2=2。
由上例可以得到如下的结论:
向量方程:
x 1 a 1 + x 2 a 2 + ⋯ + x n a n = b x_1\boldsymbol a_1 + x_2\boldsymbol a_2 + \cdots + x_n\boldsymbol a_n = \boldsymbol b x1a1+x2a2+⋯+xnan=b
和增广矩阵为:
[ a 1 a 2 ⋯ a n b ] [\boldsymbol a_1\quad \boldsymbol a_2\quad \boldsymbol \cdots \quad \boldsymbol a_n \quad \boldsymbol b] [a1a2⋯anb]
的线性方程组有相同的解集。特别的, b \boldsymbol b b可表示为 a 1 , a 2 , ⋯ , a n \boldsymbol a_1, \boldsymbol a_2, \boldsymbol \cdots, \boldsymbol a_n a1,a2,⋯,an的线性组合当且仅当对应于上述线性方程组有解。
线性代数的一个主要思想是研究可以表示为某一固定向量集合 { v 1 , v 2 , ⋯ , v n } \{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_n\} {v1,v2,⋯,vn}的线性组合的所有向量。
张成的向量集合
定义:
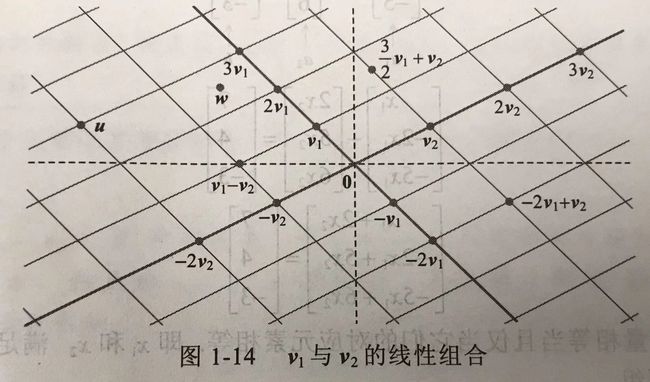
若 v 1 , v 2 , ⋯ , v n \boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_n v1,v2,⋯,vn是 R n \mathbb{R}^n Rn中的向量,则 v 1 , v 2 , ⋯ , v n \boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_n v1,v2,⋯,vn的所有线性组合所成的集合用记号 S p a n { v 1 , v 2 , ⋯ , v p } Span\{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p\} Span{v1,v2,⋯,vp}表示,称为由 v 1 , v 2 , ⋯ , v n \boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_n v1,v2,⋯,vn所生成(或张成)的 R n \mathbb{R}^n Rn的子集。也就是说, S p a n { v 1 , v 2 , ⋯ , v p } Span\{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p\} Span{v1,v2,⋯,vp}是所有形如
c 1 v 1 + c 2 v 2 + ⋯ + c p v P c_1\boldsymbol v_1 + c_2\boldsymbol v_2 + \cdots + c_p\boldsymbol v_P c1v1+c2v2+⋯+cpvP
的向量的集合,其中 c 1 , c 2 , ⋯ , c p c_1, c_2, \cdots, c_p c1,c2,⋯,cp为标量。
要判断向量 b \boldsymbol b b是否属于 S p a n { v 1 , v 2 , ⋯ , v p } Span\{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p\} Span{v1,v2,⋯,vp},就是判断方程
x 1 v 1 + x 2 v 2 + ⋯ + x p v p = b x_1\boldsymbol v_1 + x_2\boldsymbol v_2 + \cdots + x_p\boldsymbol v_p = \boldsymbol b x1v1+x2v2+⋯+xpvp=b
是否有解,或等价的,判断增广矩阵 [ v 1 v 2 ⋯ v p b ] \begin{bmatrix}\boldsymbol v_1 & \boldsymbol v_2 & \cdots & \boldsymbol v_p & \boldsymbol b\end{bmatrix} [v1v2⋯vpb]的线性方程组是否有解。
由以上定义,得出两个结论:
- S p a n { v 1 , v 2 , ⋯ , v p } Span\{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p\} Span{v1,v2,⋯,vp}包含 v 1 , v 2 , ⋯ , v p \boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p v1,v2,⋯,vp中任意一个向量的倍数。以 v 1 \boldsymbol v_1 v1为例,用 c v 1 c\boldsymbol v_1 cv1表示任意 v 1 \boldsymbol v_1 v1的倍数,那么因为 c v 1 = c v 1 + 0 v 2 + ⋯ + 0 v p c\boldsymbol v_1 = c\boldsymbol v_1 + 0\boldsymbol v_2 + \cdots + 0\boldsymbol v_p cv1=cv1+0v2+⋯+0vp,所以该结论成立。
- S p a n { v 1 , v 2 , ⋯ , v p } Span\{\boldsymbol v_1, \boldsymbol v_2, \cdots, \boldsymbol v_p\} Span{v1,v2,⋯,vp}一定包含 0 \boldsymbol 0 0向量。这时由于 0 = 0 v 1 + 0 v 2 + ⋯ + 0 v p \boldsymbol 0 = 0\boldsymbol v_1 + 0\boldsymbol v_2 + \cdots + 0\boldsymbol v_p 0=0v1+0v2+⋯+0vp。
S p a n { v } Span\{\boldsymbol v\} Span{v}与 S p a n { u , v } Span\{\boldsymbol u, \boldsymbol v\} Span{u,v}的几何解释
假设 v \boldsymbol v v是 R 3 \mathbb{R}^3 R3中的向量,那么 S p a n { v } Span\{\boldsymbol v\} Span{v}就是 v \boldsymbol v v的所有标量倍数的集合,也就是 R 3 \mathbb{R}^3 R3中通过 v \boldsymbol v v和 0 \boldsymbol 0 0的直线上所有点的集合。
若 u \boldsymbol u u和 v \boldsymbol v v是 R 3 \mathbb{R}^3 R3中的非零向量, v \boldsymbol v v不是 u \boldsymbol u u的倍数,则 S p a n { u , v } Span\{\boldsymbol u, \boldsymbol v\} Span{u,v}是 R 3 \mathbb{R}^3 R3中包含 u \boldsymbol u u, v \boldsymbol v v和 0 \boldsymbol 0 0的平面。特别的, S p a n { u , v } Span\{\boldsymbol u, \boldsymbol v\} Span{u,v}包含 R 3 \mathbb{R}^3 R3中通过 u \boldsymbol u u与 0 \boldsymbol 0 0的直线,也包含通过 v \boldsymbol v v与 0 \boldsymbol 0 0的直线(由上面的结论也可以得知这一点)。
思考:对于一个三行两列的线性方程组,其系数由 R 3 \mathbb R^3 R3中的两列向量组成,那么这两个向量的线性组合的集合最多只可能是一个平面(如果共线的话,可能只是一条直线),不可能扩张到整个 R 3 \mathbb R^3 R3。

还有一点需要注意的是,虽然 S p a n { v } Span\{\boldsymbol v\} Span{v}只是一条线, S p a n { u , v } Span\{\boldsymbol u, \boldsymbol v\} Span{u,v}只是一个平面,但并不是说 S p a n { v } Span\{\boldsymbol v\} Span{v}就属于 R 1 \mathbb{R}^1 R1, S p a n { u , v } Span\{\boldsymbol u, \boldsymbol v\} Span{u,v}就属于 R 2 \mathbb{R}^2 R2了,它们仍属于 R 3 \mathbb{R}^3 R3,是 R 3 \mathbb{R}^3 R3的一个子集而已。
在实际应用中向量和向量组合的意义
设公司生产两种产品,对于1美元价值的产品 B B B,公司需耗费0.45美元材料,0.25美元劳动,0.15美元管理费用。对1美元价值的产品 C C C,公司耗费0.40美元材料,0.30美元劳动,0.15美元管理费用。设:
b = [ 0.45 0.25 0.15 ] , c = [ 0.40 0.30 0.15 ] \boldsymbol b = \begin{bmatrix} 0.45 \\ 0.25 \\ 0.15 \end{bmatrix},\quad \boldsymbol c = \begin{bmatrix} 0.40 \\ 0.30 \\ 0.15 \end{bmatrix} b=⎣⎡0.450.250.15⎦⎤,c=⎣⎡0.400.300.15⎦⎤
则 b \boldsymbol b b和 c \boldsymbol c c称为两种产品的“单位美元产出成本”。
- 向量 100 b 100\boldsymbol b 100b的经济解释是生产100美元的产品 B B B需要的各种成本,即45美元材料、25美元劳动、15美元管理费用。
- 如果公司希望生产 x 1 x_1 x1美元产品 B B B和 x 2 x_2 x2美元产品 C C C,那么公司花费的总成本是 x 1 b 1 + x 2 b 2 x_1\boldsymbol b_1 + x_2\boldsymbol b_2 x1b1+x2b2
由这个例子,可以体悟到, R n \mathbb{R}^n Rn中的 n n n,也就是维度,可以代表现实中事物的不同方面(或者成分)。不同的向量可以代表做一件简单事情(或称基本事件,元事件)时,各个方面是如何配合的。而这些向量的组合(也是一个向量),又可以代表做一件复杂的事情时,如何由元事件搭配起来。