行列式相关定理《线性代数》学习笔记)
行列式相关定理
- 行列式的余子式
- 行列式的代数余子式
- 行列式的按行展开
- 异乘变零定理
- 拉普拉斯展开定理
- 行列式相乘定理
- 参考文献
行列式的余子式
行列式去掉某一元素 a i j a_{ij} aij的所在行和所在列,剩余的子集仍然是行列式。我们通常称这个行列式为:余子式,记作 M i j M_{ij} Mij。
以三阶行列式为例:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ \begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} ∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣
元素 a 11 a_{11} a11的余子式 M 11 M_{11} M11是去掉第一行、第一列后,剩余的子集:
M 11 = ∣ a 22 a 23 a 32 a 33 ∣ M_{11}=\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} M11=∣∣∣∣a22a32a23a33∣∣∣∣
小练习
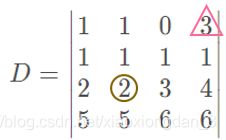
对于三角框中的元素“3”,其余子式可写作 M 14 = ∣ 1 1 1 2 2 3 5 5 6 ∣ M_{14}=\begin{vmatrix} 1 & 1&1 \\ 2 & 2& 3\\5&5&6 \end{vmatrix} M14=∣∣∣∣∣∣125125136∣∣∣∣∣∣
对于圆形框中的元素“2”,其余子式可写作 M 32 = ∣ 1 0 3 1 1 1 5 6 6 ∣ M_{32}=\begin{vmatrix} 1 & 0&3 \\ 1 & 1& 1\\5&6&6 \end{vmatrix} M32=∣∣∣∣∣∣115016316∣∣∣∣∣∣
行列式的代数余子式
简单来说,就是带符号的余子式。元素 a i j a_{ij} aij的代数余子式为 ( − 1 ) i + j × M i j (-1)^{i+j}×M_{ij} (−1)i+j×Mij,符号记作 A i j A_{ij} Aij。
以三阶行列式为例:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ \begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} ∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣
元素 a 11 a_{11} a11的代数余子式 A 11 A_{11} A11写作:
A 11 = ( − 1 ) 1 + 1 × M 11 = ( − 1 ) 1 + 1 × ∣ a 22 a 23 a 32 a 33 ∣ A_{11}=(-1)^{1+1}×M_{11}=(-1)^{1+1}×\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} A11=(−1)1+1×M11=(−1)1+1×∣∣∣∣a22a32a23a33∣∣∣∣
小练习
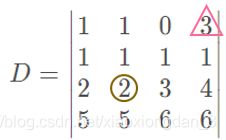
对于三角框中的元素“3”,其余子式可写作 A 14 = ( − 1 ) 1 + 4 × M 14 = ( − 1 ) 1 + 4 × ∣ 1 1 1 2 2 3 5 5 6 ∣ A_{14}=(-1)^{1+4}×M_{14}=(-1)^{1+4}×\begin{vmatrix} 1 & 1&1 \\ 2 & 2& 3\\5&5&6 \end{vmatrix} A14=(−1)1+4×M14=(−1)1+4×∣∣∣∣∣∣125125136∣∣∣∣∣∣
对于圆形框中的元素“2”,其余子式可写作 A 32 = ( − 1 ) 3 + 2 × M 32 = ( − 1 ) 3 + 2 × ∣ 1 0 3 1 1 1 5 6 6 ∣ A_{32}=(-1)^{3+2}×M_{32}=(-1)^{3+2}×\begin{vmatrix} 1 & 0&3 \\ 1 & 1& 1\\5&6&6 \end{vmatrix} A32=(−1)3+2×M32=(−1)3+2×∣∣∣∣∣∣115016316∣∣∣∣∣∣
行列式的按行展开
行列式任意一行的各元素和其对应的代数余子式的乘积之和。
D = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ D=\begin{vmatrix}a_{11} & a_{12}& \cdots&a_{1n}\\a_{21} & a_{22}&\cdots& a_{2n}\\\vdots &\vdots& \ddots&\vdots\\ a_{n1} & a_{n2}& \cdots&a_{nn}\end{vmatrix} D=∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣
对于 n n n阶行列式,其按第 i i i行展开为:

小练习
写出行列式 D = ∣ 1 1 2 0 1 0 2 3 5 ∣ D=\begin{vmatrix} 1 & 1&2 \\ 0 & 1& 0\\2&3&5 \end{vmatrix} D=∣∣∣∣∣∣102113205∣∣∣∣∣∣的按行展开。
-
答案 1:

按第1行展开: D = 1 × ( − 1 ) 1 + 1 × ∣ 1 0 3 5 ∣ + 1 × ( − 1 ) 1 + 2 × ∣ 0 0 2 5 ∣ + 1 × ( − 1 ) 1 + 3 × ∣ 0 1 2 3 ∣ D=1×(-1)^{1+1}×\begin{vmatrix} 1& 0\\3&5 \end{vmatrix}+1×(-1)^{1+2}×\begin{vmatrix} 0& 0\\2&5 \end{vmatrix}+1×(-1)^{1+3}×\begin{vmatrix} 0& 1\\2&3 \end{vmatrix} D=1×(−1)1+1×∣∣∣∣1305∣∣∣∣+1×(−1)1+2×∣∣∣∣0205∣∣∣∣+1×(−1)1+3×∣∣∣∣0213∣∣∣∣ -
答案 2:

按第2行展开: D = 1 × ( − 1 ) 2 + 2 × ∣ 1 2 2 5 ∣ D=1×(-1)^{2+2}×\begin{vmatrix} 1& 2\\2&5 \end{vmatrix} D=1×(−1)2+2×∣∣∣∣1225∣∣∣∣ -
答案 3:

按第3行展开: D = 1 × ( − 1 ) 1 + 1 × ∣ 1 0 3 5 ∣ + 1 × ( − 1 ) 1 + 2 × ∣ 0 0 2 5 ∣ + 1 × ( − 1 ) 1 + 3 × ∣ 0 1 2 3 ∣ D=1×(-1)^{1+1}×\begin{vmatrix} 1& 0\\3&5 \end{vmatrix}+1×(-1)^{1+2}×\begin{vmatrix} 0& 0\\2&5 \end{vmatrix}+1×(-1)^{1+3}×\begin{vmatrix} 0& 1\\2&3 \end{vmatrix} D=1×(−1)1+1×∣∣∣∣1305∣∣∣∣+1×(−1)1+2×∣∣∣∣0205∣∣∣∣+1×(−1)1+3×∣∣∣∣0213∣∣∣∣
通过上述例子,我们可以发现行列式按行展开的两大特点:1)按行展开有降阶的效果(例题中由三阶行列式变为了二阶行列式);2)在做行列式展开式,尽量选择“0”多的一行展开(例题中答案2中只需要一项即可写完,其余答案都得写多项)。
注:行列式的按列展开与按行展开类似:行列式任意一列的各元素和其对应的代数余子式的乘积之和。
对于 n n n阶行列式,其按第 i i i列展开为: D = a i 1 A i 1 + a i 2 A i 2 + … + a i n A i n D=a_{i1}A_{i1}+a_{i2}A_{i2}+…+a_{in}A_{in} D=ai1Ai1+ai2Ai2+…+ainAin
异乘变零定理
行列式某行元素与另一行元素的代数余子式乘积之和为零。
以三阶行列式为例进行证明: D = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ D=\begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} D=∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣求第3行元素与第1行元素的代数余子式的乘积之和: D = a 31 × A 11 + a 32 × A 12 + a 33 × A 13 ① D=a_{31} ×A_{11}+a_{32} ×A_{12}+a_{33} ×A_{13} \ \ \ \ \ ① D=a31×A11+a32×A12+a33×A13 ① 对于一个新的三阶行列式(第3行和第1行相等) D ′ = ∣ a 31 a 32 a 33 a 21 a 22 a 23 a 31 a 32 a 33 ∣ D'=\begin{vmatrix} a_{31} & a_{32} & a_{33} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} D′=∣∣∣∣∣∣a31a21a31a32a22a32a33a23a33∣∣∣∣∣∣求第3行元素与第1行元素的代数余子式的乘积之和: D ′ = a 31 × A 11 + a 32 × A 12 + a 33 × A 13 ② D'=a_{31} ×A_{11}+a_{32} ×A_{12}+a_{33}×A_{13} \ \ \ \ \ ② D′=a31×A11+a32×A12+a33×A13 ② 观察 ① 和 ②,他们的值其实是一样的,即 D = D ′ D=D' D=D′,又由行列式性质2的推论(见上一篇文章),可以知道 D ′ = 0 D'=0 D′=0,因此 D = 0 D=0 D=0,即证得该定理。
拉普拉斯展开定理
在看这个定理之前,我们先来学习一组概念。
- k k k阶子式:取定 k k k行、 k k k列,取出位于划线交叉位置处的元素组成的行列式。
- k k k阶子式的余子式:取定 k k k行、 k k k列,取出未被划线位置处的元素组成的行列式。
- - k k k阶子式的代数余子式:在余子式的概念上增加了符号(-1的指数为取出的所有的第几行、第几列数字之和)。
2阶子式:当 k = 2 k=2 k=2时,取定任意两行、两列取出位于划线交叉位置处的元素组成的行列式。
2阶子式的余子式:当 k = 2 k=2 k=2时,取定任意两行、两列取出未被划线位置处的元素组成的行列式。
2阶子式的代数余子式:当 k = 2 k=2 k=2时,在余子式的概念上增加了符号(-1的指数为取出的两个第几行、两个第几列数字之和)。
例如: 对于四阶行列式:
D = ∣ 1 1 0 3 1 1 1 1 2 2 3 4 5 5 6 6 ∣ D=\begin{vmatrix} 1 & 1 & 0 & 3 \\1 & 1 & 1 & 1 \\ 2 & 2 & 3 & 4 \\ 5 & 5 & 6 & 6 \end{vmatrix} D=∣∣∣∣∣∣∣∣1125112501363146∣∣∣∣∣∣∣∣
当取定1、2行和1、2列时,它的2阶子式是:
它的2阶子式的余子式是:
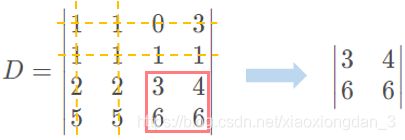
它的2阶子式的余子式是:

有了这样一些前序知识铺垫,我们再来看看什么是拉普拉斯展开定理。
拉普拉斯展开定理:取定 k k k行,由 k k k行元素组成的所有阶子式与代数余子式乘积之和等于行列式的值。
在一些特殊的行列式中,应用该定理展开行列式,会显得非常方便。
例如: 对于五阶行列式
D = ∣ 1 2 0 0 0 3 4 0 0 0 1 2 3 4 5 5 4 1 2 2 3 1 1 2 3 ∣ D=\begin{vmatrix} 1& 2& 0& 0& 0\\3&4& 0& 0& 0\\1&2& 3& 4& 5\\5&4& 1& 2& 2\\3&1& 1& 2& 3\end{vmatrix} D=∣∣∣∣∣∣∣∣∣∣1315324241003110042200523∣∣∣∣∣∣∣∣∣∣ 如果我们要将 D D D展开,运用通常的方式会相当复杂。我们观察到该行列式的第1、2行有很多“0”,我们可以使用拉普拉斯展开定理,选定第1、2行,再取出第1、2列(因为后面三列都是0,如果取后面三列的任意一列与其他列组合,得到的2阶子式的值都是0。所以为了方便运算,直接取前两列)。

因此,根据拉普拉斯定理, D D D的展开式写作:
D = ∣ 1 2 3 4 ∣ × ( − 1 ) 1 + 2 + 1 + 2 ∣ 3 4 5 1 1 1 8 3 1 ∣ D=\begin{vmatrix} 1& 2\\3&4 \end{vmatrix}×(-1)^{1+2+1+2}\begin{vmatrix} 3& 4&5\\1&1&1\\8&3&1 \end{vmatrix} D=∣∣∣∣1324∣∣∣∣×(−1)1+2+1+2∣∣∣∣∣∣318413511∣∣∣∣∣∣
行列式相乘定理
假设 D 1 D_1 D1、 D 2 D_2 D2是两个 n n n阶行列式,则它的乘积可以表示成一个 n n n阶行列式。
例如: D 1 = ∣ 1 2 3 2 0 0 0 1 3 ∣ D_1=\begin{vmatrix} 1& 2&3\\2&0&0\\0&1&3 \end{vmatrix} D1=∣∣∣∣∣∣120201303∣∣∣∣∣∣、 D 2 = ∣ 4 1 3 5 3 2 6 1 0 ∣ D_2=\begin{vmatrix} 4& 1&3\\5&3&2\\6&1&0 \end{vmatrix} D2=∣∣∣∣∣∣456131320∣∣∣∣∣∣,计算 D 1 × D 2 D_1×D_2 D1×D2。
计算原则: D 1 D_1 D1的第 i i i行和 D 2 D_2 D2的第 j j j列的对应元素相乘再相加,得到结果行列式的元素 a i j a_{ij} aij。
以计算 D 1 × D 2 D_1×D_2 D1×D2的元素 a 11 a_{11} a11为例: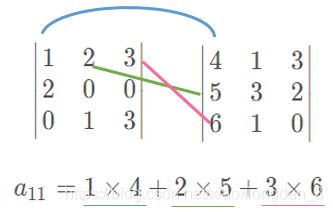
因此 D 1 × D 2 = ∣ 32 10 7 8 2 6 23 6 2 ∣ D_1×D_2=\begin{vmatrix} 32& 10&7\\8&2&6\\23&6&2 \end{vmatrix} D1×D2=∣∣∣∣∣∣328231026762∣∣∣∣∣∣
小思考
1)上面提到的两个行列式相乘,都是同阶的行列式相乘。那么对不同阶的行列式相乘,这种方法还使用吗?
当然不适用(原因自己想吧,码字真的好累啊,枯了)。
2)不同阶的行列式可以相乘吗?
当然可以!你可以将两个行列式的值分别求出,这样就变成了两个数相乘;也可以对高阶行列式降阶(前面提到的按行展开),这样就变成了同阶行列式相乘。
参考文献
[1]宋浩.《线性代数》高清教学视频 “惊叹号”系列 宋浩老师[EB/OL].https://www.bilibili.com/video/BV1aW411Q7x1?p=4,2019-06-12.
上篇笔记地址→ 行列式性质