csp刷题记录201312
零基础的算法小白要开始刷csp了,做一只不那么躺的咸鱼!
long long ago从第一套题开始
顺便吐槽一下,古早的csp题跟现在的csp套路完全不一样啊
第一题
201312-1 出现次数最多的数
问题描述
给定n个正整数,找出它们中出现次数最多的数。如果这样的数有多个,请输出其中最小的一个。
输入格式
输入的第一行只有一个正整数n(1 ≤ n ≤ 1000),表示数字的个数。
输入的第二行有n个整数s1, s2, …, sn (1 ≤ si ≤ 10000, 1 ≤ i ≤ n)。相邻的数用空格分隔。
输出格式
输出这n个次数中出现次数最多的数。如果这样的数有多个,输出其中最小的一个。
样例输入
6
10 1 10 20 30 20
样例输出
10
按照题意输出即可
造了一个结构体,结构体中储存了每个数的数值和出现的次数
然后sort一下就好
#include
using namespace std;
const int maxn=10005;
struct node
{
int num;
int cnt;
}Node[maxn];
bool cmp(node a,node b)
{
if(a.cnt==b.cnt)
{
return a.numb.cnt;
}
int main()
{
int n,temp;
cin>>n;
for(int i=0;i>temp;
Node[temp].cnt++;
Node[temp].num=temp;
}
sort(Node,Node+maxn,cmp);
cout< 第二题 ISBN号码
201312-2
问题描述
每一本正式出版的图书都有一个ISBN号码与之对应,ISBN码包括9位数字、1位识别码和3位分隔符,其规定格式如“x-xxx-xxxxx-x”,其中符号“-”是分隔符(键盘上的减号),最后一位是识别码,例如0-670-82162-4就是一个标准的ISBN码。ISBN码的首位数字表示书籍的出版语言,例如0代表英语;第一个分隔符“-”之后的三位数字代表出版社,例如670代表维京出版社;第二个分隔之后的五位数字代表该书在出版社的编号;最后一位为识别码。
识别码的计算方法如下:
首位数字乘以1加上次位数字乘以2……以此类推,用所得的结果mod 11,所得的余数即为识别码,如果余数为10,则识别码为大写字母X。例如ISBN号码0-670-82162-4中的识别码4是这样得到的:对067082162这9个数字,从左至右,分别乘以1,2,…,9,再求和,即0×1+6×2+……+2×9=158,然后取158 mod 11的结果4作为识别码。
编写程序判断输入的ISBN号码中识别码是否正确,如果正确,则仅输出“Right”;如果错误,则输出是正确的ISBN号码。输入格式 输入只有一行,是一个字符序列,表示一本书的ISBN号码(保证输入符合ISBN号码的格式要求)。输出格式 输出一行,假如输入的ISBN号码的识别码正确,那么输出“Right”,否则,按照规定的格式,输出正确的ISBN号码(包括分隔符“-”)。
样例输入
0-670-82162-4
样例输出
Right
样例输入
0-670-82162-0
样例输出
0-670-82162-4
简单的字符串模拟题,照题意模拟就行
#include
using namespace std;
char str[13];
int main()
{
cin>>str;
int cnt=0,result=0;
for(int i=0;i<=10;i++)
{
if(str[i]>='0'&&str[i]<='9')
{
cnt++;
result+=(cnt*(str[i]-'0'));
}
}
result=result%11;
if(result==(str[12]-'0')||(result==10 && str[12]=='X'))
{
cout<<"Right"< 第三题 最大的矩形
201312-3
问题描述
在横轴上放了n个相邻的矩形,每个矩形的宽度是1,而第i(1 ≤ i ≤ n)个矩形的高度是hi。这n个矩形构成了一个直方图。例如,下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。
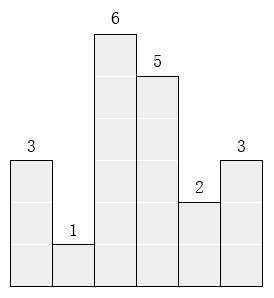
请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是10。
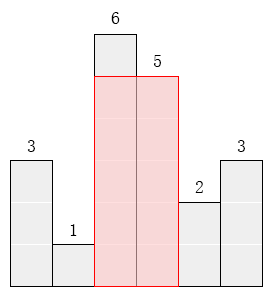
输入格式
第一行包含一个整数n,即矩形的数量(1 ≤ n ≤ 1000)。
第二行包含n 个整数h1, h2, … , hn,相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
输出一行,包含一个整数,即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10
这个题,第一反应是暴力,然后写了交上去,然后就过了orz
遍历所有的区间和,找出每一段区间和中最短的Min
Min乘以 每一段区间长
然后比较找出最大值即可
看了一下别人的解法,据说这是一道单调栈题的模板
过几天学一下单调栈并且把这个题的单调栈解法贴出来(flag立下
#include
using namespace std;
int a[1005];
int main()
{
int n;
cin>>n;
for(int i=0;i>a[i];
}
int ans=0;
for(int i=0;i 第四题 有趣的数
201312-4
问题描述
我们把一个数称为有趣的,当且仅当
- 它的数字只包含0, 1, 2, 3,且这四个数字都出现过至少一次。
- 所有的0都出现在所有的1之前,而所有的2都出现在所有的3之前。
- 最高位数字不为0。
因此,符合我们定义的最小的有趣的数是2013。除此以外,4位的有趣的数还有两个:2031和2301。
请计算恰好有n位的有趣的数的个数。由于答案可能非常大,只需要输出答案除1000000007的余数。
输入格式
输入只有一行,包括恰好一个正整数n (4 ≤ n ≤ 1000)。
输出格式
输出只有一行,包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。
样例输入
4
样例输出
3
一看到dp题就懵逼ing (抽空要练习数位dp
首先,一共有六种情况
1.只有2出现
2.只有2,0出现
3.只有2,3出现
4.只有2,0,1出现
5.只有2,0,3出现
6.所有的数2,0,1,3都出现(题目所要求的
分析可知
第一种情况
只有一种可能 dp[i][0]=1
第二种情况
有两种可能:
前i-1位中只有2出现+末尾0
前i-1位中2,0出现+末尾0或者2
所以 dp[i][1]=dp[i][0]+dp[i-1][1]*2
第三种情况
有两种可能:
前i-1位中只有2出现+末尾3
前i-1位中2,3出现+末尾3
所以 dp[i][2]=dp[i][0]+dp[i-1][2]
第四种情况
有两种可能:
前i-1位中有2,0出现+末尾1
前i-1位中有2,0,1出现+末尾2或1
所以dp[i][3]=dp[i-1][1]+dp[i-1][3]*2
第五种情况
有三种可能:
前i-1位中有2,0出现+末尾3
前i-1位中有2,3出现+末尾0
前i-1位中有2,0,3出现+末尾0或3
所以dp[i][4]=dp[i-1][1]+dp[i-1][2]+dp[i-1][4]*2
第六种情况
有三种可能:
前i-1位中有2,0,1出现+末尾3
前i-1位中有2,0,3出现+末尾1
前i-1位中有2,0,1,3出现+末尾1或3
所以dp[i][5]=dp[i-1][3]+dp[i-1][4]+dp[i-1][5]*2
以及取模运算的基本规律:
(a + b) % p = (a%p + b%p) %p
(a - b) % p = ((a%p - b%p) + p) %p
(a * b) % p = (a%p)*(b%p) %p
//dp[][0] 2
//dp[][1] 2 0
//dp[][2] 2,3
//dp[][3] 2,0,1
//dp[][4] 2,0,3
//dp[][5] 2,0,1,3
#include
using namespace std;
const int mod=1000000007;
long long dp[1005][6];
int main()
{
int n;
cin>>n;
dp[0][0]=1;
for(int i=1;i 第五题 I‘m stuck
201312-5
问题描述
给定一个R行C列的地图,地图的每一个方格可能是’#’, ‘+’, ‘-’, ‘|’, ‘.’, ‘S’, ‘T’七个字符中的一个,分别表示如下意思:
‘#’: 任何时候玩家都不能移动到此方格;
‘+’: 当玩家到达这一方格后,下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格;
‘-’: 当玩家到达这一方格后,下一步可以向左右两个方向相邻的一个非’#‘方格移动一格;
‘|’: 当玩家到达这一方格后,下一步可以向上下两个方向相邻的一个非’#‘方格移动一格;
‘.’: 当玩家到达这一方格后,下一步只能向下移动一格。如果下面相邻的方格为’#’,则玩家不能再移动;
‘S’: 玩家的初始位置,地图中只会有一个初始位置。玩家到达这一方格后,下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格;
‘T’: 玩家的目标位置,地图中只会有一个目标位置。玩家到达这一方格后,可以选择完成任务,也可以选择不完成任务继续移动。如果继续移动下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格。
此外,玩家不能移动出地图。
请找出满足下面两个性质的方格个数:
1. 玩家可以从初始位置移动到此方格;
2. 玩家不可以从此方格移动到目标位置。输入格式 输入的第一行包括两个整数R 和C,分别表示地图的行和列数。(1 ≤ R, C ≤ 50)。
接下来的R行每行都包含C个字符。它们表示地图的格子。地图上恰好有一个’S’和一个’T’。
输出格式
如果玩家在初始位置就已经不能到达终点了,就输出“I’m stuck!”(不含双引号)。
否则的话,输出满足性质的方格的个数。
样例输入
5 5
–±+
…|#.
…|##
S-±T
####.
样例输出
2
样例说明
如果把满足性质的方格在地图上用’X’标记出来的话,地图如下所示:
–±+
…|#X
…|##
S-±T
####X
开始觉得是个简单的dfs题,后来卡在反向dfs好久ing……
具体思路不难,
先正向dfs一遍,标记出所有S点能到的点
再反向dfs一遍标记处所有能到T点的点
#include
using namespace std;
int m,n;
char mp[55][55];
int svis[55][55],tvis[55][55];
void dfs(int x,int y)
{
if(x<0||x>=m||y<0||y>=n) return;
if(mp[x][y]=='#'||svis[x][y])
{
return;
}
svis[x][y]=1;
if(mp[x][y]=='+'||mp[x][y]=='S'||mp[x][y]=='T')
{
dfs(x+1,y);
dfs(x-1,y);
dfs(x,y+1);
dfs(x,y-1);
}
if(mp[x][y]=='-')
{
dfs(x,y+1);
dfs(x,y-1);
}
if(mp[x][y]=='|')
{
dfs(x+1,y);
dfs(x-1,y);
}
if(mp[x][y]=='.')
{
dfs(x+1,y);
}
}
void DDfs(int x,int y,int p1,int p2)//反向dfs
{
if(mp[x][y]=='#'|| tvis[x][y]==1 ) return;
if(mp[x][y]=='.'&&p1==x+1&&p2==y)
{
tvis[x][y]=1;
}
else if(mp[x][y]=='-'&&x==p1)
{
tvis[x][y]=1;
}
else if(mp[x][y]=='|'&&y==p2)
{
tvis[x][y]=1;
}
else if(mp[x][y]=='S'||mp[x][y]=='T'||mp[x][y]=='+')
{
tvis[x][y]=1;
}
if(tvis[x][y]==0) return;
if(x>0) DDfs(x-1,y,x,y);
if(y>0) DDfs(x,y-1,x,y);
if(x>m>>n;
int s1,s2,t1,t2;
for(int i=0;i>mp[i][j];
if(mp[i][j]=='S')
{
s1=i;
s2=j;
}
else if(mp[i][j]=='T')
{
t1=i;
t2=j;
}
}
}
dfs(s1,s2);
if(!svis[t1][t2])
{
cout<<"I'm stuck!"<