贝叶斯分类的基础——贝叶斯定理
贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
这个定理解决了现实生活里经常遇到的问题:已知某条件概率(概率密度函数),如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率:
![]() 表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:![]() 。
。
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
下面不加证明地直接给出贝叶斯定理:
![]()
朴素贝叶斯的推导:
朴素贝叶斯的三个常用模型:高斯、多项式、伯努利
1)多项式模型
举例:
2)高斯模型
3)伯努利模型
朴素贝叶斯分类的原理与流程:
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的正式定义如下:
1、设![]() 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合![]() 。
。
3、计算![]() 。
。
4、如果![]() ,则
,则![]() 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即![]() 。
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
![]()
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
![]()
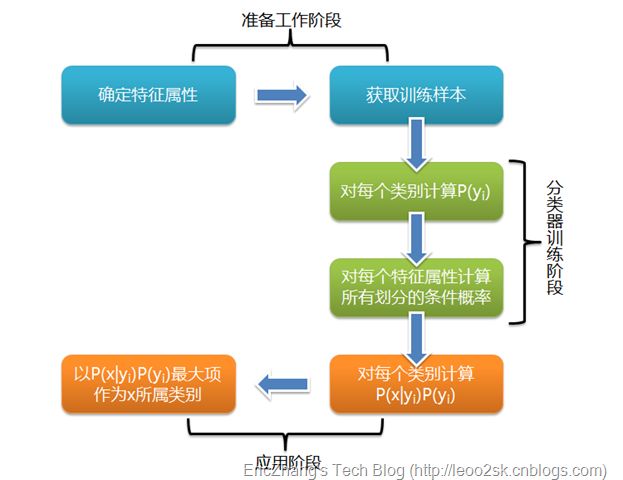
可以看到,整个朴素贝叶斯分类分为三个阶段:
第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
参考:
http://blog.csdn.net/u012162613/article/details/48323777
http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html