机器学习入门--朴素贝叶斯原理与实践
朴素贝叶斯算法
朴素贝叶斯是一种常用的分类算法,其基本思想是根据已有数据的特征和标签,学习出一个概率模型,并利用该模型对新样本进行分类。其优点在于简单快速、易于实现和解释,缺点在于对输入数据的分布做了严格的假设。
具体来说,朴素贝叶斯分类器首先根据训练数据计算出每个类别的先验概率P©,即样本中每个类别占比。然后,对于给定的待分类样本,计算出它属于每个类别的条件概率P(X|C),其中X表示样本的特征向量,C表示类别。根据贝叶斯定理,可以计算出样本属于每个类别的后验概率P(C|X),并选择后验概率最大的类别作为预测结果。
在实际应用中,朴素贝叶斯分类器常用于文本分类、垃圾邮件过滤、情感分析等任务。可以使用sklearn中的NaiveBayes对象进行实现,具体步骤包括导入数据、创建模型、训练模型、预测结果和评估模型性能。
朴素贝叶斯算法的数学原理
朴素贝叶斯算法基于贝叶斯定理,通过计算样本的后验概率来进行分类。其数学原理如下:
贝叶斯定理
贝叶斯定理是概率论中一个重要的定理,用于计算在给定一些观察数据的前提下,某个事件的概率。对于两个事件A和B,贝叶斯定理可以表示为:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A) P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
其中, P ( A ∣ B ) P(A|B) P(A∣B)是在观察到事件 B B B发生的情况下,事件 A A A发生的概率; P ( B ∣ A ) P(B|A) P(B∣A)是在事件 A A A发生的情况下,观察到事件 B B B发生的概率; P ( A ) P(A) P(A)和 P ( B ) P(B) P(B)分别是事件A和事件 B B B的独立概率。
朴素贝叶斯原理
朴素贝叶斯算法假设特征之间相互独立,并且每个特征对于分类结果具有相同的重要性。基于这些假设,我们可以将贝叶斯定理应用于分类问题。
假设有一个待分类样本 X X X,它包含 n n n个特征的特征向量 ( x 1 , x 2 , ⋯ , x n ) (x_{1}, x_{2}, \cdots, x_{n}) (x1,x2,⋯,xn)。我们将样本分为 k k k个不同的类别 c 1 , c 2 , ⋯ , c n c_{1}, c_{2}, \cdots, c_{n} c1,c2,⋯,cn。朴素贝叶斯算法要求特征之间相互独立。根据贝叶斯定理,我们可以计算样本 X X X属于每个类别 C i C_{i} Ci的后验概率 P ( C i ∣ X ) P(C_{i}|X) P(Ci∣X):
P ( C i ∣ X ) = P ( X ∣ C i ) P ( C i ) P ( X ) P(C_{i}|X) = \frac{P(X|C_{i})P(Ci)}{P(X)} P(Ci∣X)=P(X)P(X∣Ci)P(Ci)
其中, P ( C i ∣ X ) P(C_{i}|X) P(Ci∣X)表示给定样本 X X X后属于类别 C i C_{i} Ci的概率, P ( X ∣ C i ) P(X|C_{i}) P(X∣Ci)表示样本 X X X在类别 C i C_{i} Ci下的特征条件概率, P ( C i ) P(C_{i}) P(Ci)表示类别 C i C_{i} Ci的先验概率, P ( X ) P(X) P(X)表示样本 X X X的边缘概率。
高斯贝叶斯分类器(GaussianNB)
高斯贝叶斯分类器是朴素贝叶斯算法的一种常见变种,适用于连续特征的分类问题。
在高斯贝叶斯分类器中,假设样本特征的条件概率服从高斯分布。具体来说,对于每个特征 x i x_{i} xi和类别 C i C_{i} Ci,我们可以通过计算训练数据中对应类别 C i C_{i} Ci的特征 x i x_{i} xi的均值 μ \mu μ和方差 σ 2 \sigma^2 σ2来估计 P ( x i ∣ C i ) P(x_{i}|C_{i}) P(xi∣Ci)。
然后,利用这些条件概率进行分类预测。
伯努利贝叶斯分类器(BernoulliNB)
伯努利贝叶斯分类器也是朴素贝叶斯算法的一种常见变种,适用于二值特征的分类问题。在伯努利贝叶斯分类器中,假设样本特征的条件概率服从伯努利分布。对于每个特征 x i x_{i} xi和类别 C i C_{i} Ci,我们计算训练数据中对应类别 C i C_{i} Ci中特征 x i x_{i} xi为1的比例 P ( x i = 1 ∣ C i ) P(x_{i}=1|C_{i}) P(xi=1∣Ci)。然后,利用这些条件概率进行分类预测。
算法的优缺点
朴素贝叶斯算法的优点包括:
- 算法简单,实现容易。
- 对小规模数据表现良好,计算速度快。
- 在处理大量特征时仍然有效,因为它假设特征之间相互独立。
朴素贝叶斯算法的缺点包括:
- 假设特征之间相互独立,这在某些情况下可能不符合实际情况。
- 对输入数据的表达形式较为敏感,对于不同的表示形式可能得到不同的结果。
- 需要预先假设特征的概率分布,这在某些情况下可能不准确。
代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
# 加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target
# 创建朴素贝叶斯分类器
clf = GaussianNB()
# 训练分类器
clf.fit(X, y)
# 预测结果
y_pred = clf.predict(X)
# 绘制分类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis')
plt.xlabel('Sepal length (cm)')
plt.ylabel('Sepal width (cm)')
plt.title('Naive Bayes Classification on Iris Dataset')
plt.show()
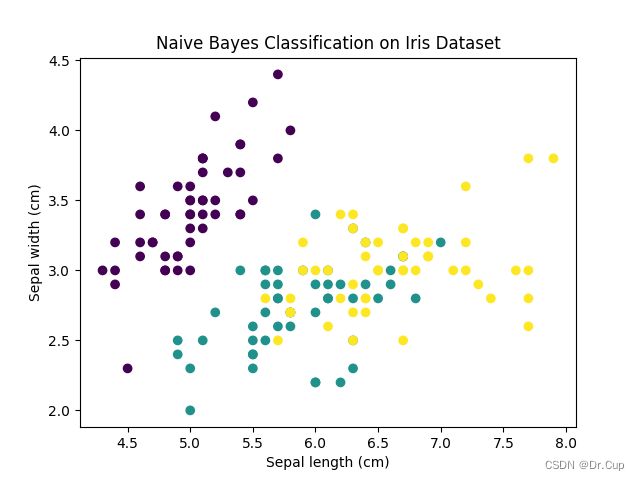
在上述代码中,我们首先使用load_iris函数加载iris数据集,然后将数据和标签存储在X和y变量中。接下来,我们创建了一个GaussianNB对象作为朴素贝叶斯分类器,并使用整个数据集进行训练。最后,我们使用分类器对数据集进行预测,并利用scatter函数将数据点按照预测结果进行可视化(如下图所示)。
总结
朴素贝叶斯算法是一种基于贝叶斯定理的分类算法,通过计算样本的后验概率来进行分类。该算法假设样本特征相互独立且重要性相同,适用于小规模数据和高效计算。总之,朴素贝叶斯算法是一种简单而强大的分类算法,适用于许多实际问题,并且具有广泛的应用前景。