Manacher算法(最长回文子串问题)
前言:
很久之前就听到shallwe大爷提到过一种叫马拉车的算法。。。
问题描述
最长回文子串问题:给定一个字符串,求它的最长回文子串长度
(注意,我们这里说的子串一定是连续的,要与子序列区分开)
如果一个字符串正着读和反着读是一样的,那它就是回文串。下面是一些回文串的实例:
12321 a aba abba aaaa tattarrattat(牛津英语词典中最长的回文单词)
暴力?
最简单粗暴的方法:我们可以找到所有子串,暴力判断是否回文
因为每一个子串是由起点和终点确定的,所有一共有n^2个子串
复杂度O(n^3)
改进一下?
回文,实际上就是中心对称
因此我们可以枚举每一个位置,作为回文子串的对称轴,每次从中心像两边扩展
这里要注意,回文串要分成两种情况:长度为奇数,长度为偶数
针对每一个位置,我们都要进行以上两种尝试
复杂度O(n^2)
好像还有n^2的方法
这么经典的问题,当然可以用dp解决啦
设f[i][j]表示从i到j的字符串是否是回文串(bool类型的)
这样我们就有转移方程:
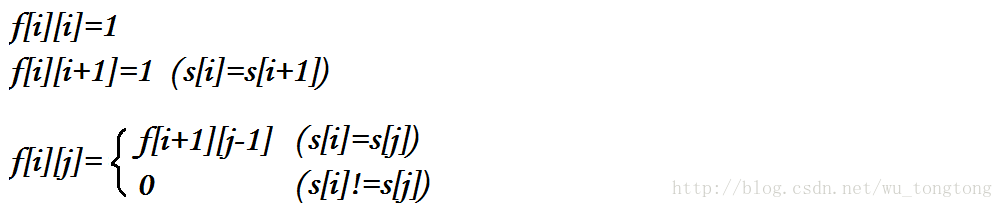
这里就不得不提一句:
最长回文子序列
经典解法就是dp,然而因为是子序列(不要求连续)
所以我们可以正反分别存储原串,做两个串的LCS即可
(LCS又可以视情况转化成LIS完成,但这就是后话了)
Manacher 算法
俗称:马拉车算法
为众位大神所青睐,是OI道路上的必备佳品
显然,对于过长的字符串,n^2的复杂度是无法承受的,所以我们需要一种更高效的算法
首先我们先研究一下n^2算法中我们都把时间浪费在了哪
- 由于回文串长度的奇偶性造成了不同性质的对称轴位置,要对两种情况分别处理;
很多子串被重复多次访问,造成较差的时间效率
简单解释一下缺陷二:char : a b a b a i : 0 1 2 3 4 //当i=1和i=2时,左边的子串aba分别被遍历了一次
如果我们能过通过某个扩展包修复这两个bug的话,就可以大大的提高效率了
(1) 解决长度奇偶性带来的对称轴位置问题
马拉车算法首先对字符串做一个预处理,
在每两个字符之间(包括首尾)插入一个相同无效字符(在原串中没有出现过),
这样就会使所有的串都是奇数长度的
aba ---> #a#b#a#
abba ---> #a#b#b#a#这样处理后,原串的回文性质不受影响
原来是回文的串仍是回文串,原来不是回文的串依然不是回文
(2) 解决重复访问的问题
我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径
Manacher定义了一个回文半径数组RL
用RL[i]表示以第i个字符为对称轴的回文串的回文半径
我们一般对字符串从左往右处理,因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离
char : # a # b # a #
RL : 1 2 1 4 1 2 1
RL-1 : 0 1 0 3 0 1 0
i : 0 1 2 3 4 5 6
char : # a # b # b # a #
RL : 1 2 1 2 5 2 1 2 1
RL-1 : 0 1 0 1 4 1 0 1 0
i : 0 1 2 3 4 5 6 7 8可以注意到,我们还写出了RL-1的值
观察一下可以发现,RL-1的值就是原串中以i为对称轴的回文串的长度
那么如果我们得到了RL数组,最长回文子串就知道了
于是现在问题变成了:如何求解RL数组(即以i为对称轴的回文串的最右端点)
原理:回文串的对称性
方法:分类讨论+暴力扩展
之前我们已经说过:对字符串一般从左往右处理
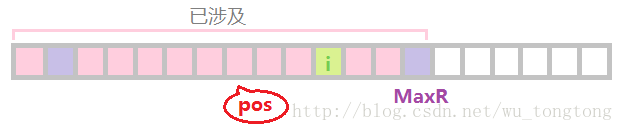
我们引入一个变量 MaxR ,表示当前访问到的所有回文子串中,涉及到的最右端点
同时记录一下该回文串的对称轴所在位置pos
因为我们是从左到右进行的
所以当前访问位置一定在pos右边
但我们更关注的是,i是在MaxRight的左边还是右边
我们分情况来讨论
1)当 i 在 MaxR 左边
两个紫色格之内的字符串是回文的,
这种情况下,以 i 为对称轴的回文串与 pos 的回文串是有一部分重合的
我们可以找到 i 关于 pos 的对称点 j
这个 j 的对应的 RL[j] 我们是计算过的
根据回文的性质,以i为对称轴的回文串和以j为对称轴的回文串会有一部分相同
这里我们又细分成两种情况:
以 j 为对称轴的回文串比较短,两端都没有超过 pos 代表的回文串
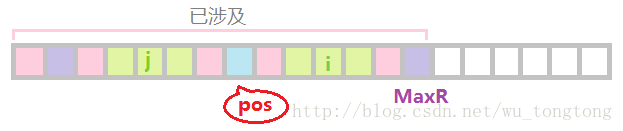
我们可以肯定,RL[i]不会小于RL[j]
并且已经知道了部分的以i为中心的回文串,于是可以令RL[i]=RL[j]
但是以i为对称轴的回文串可能实际上更长,因此我们试着以已经确定的区间为左右端点,继续往左右两边扩展,直到左右两边字符不同,或者到达边界-
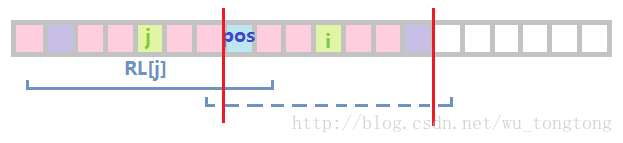
这时我们只能确定,两条红线之间的部分(即不超过MaxRight的部分)是回文的,
于是从这个长度开始,尝试向左右两边扩展,直到左右两边字符不同,或者到达边界
不论以上哪种情况,之后都要尝试更新MaxRight和pos,因为有可能得到更大的MaxRight。
1)当 i 在 MaxR 右边(包括在MarR上)
遇到这种情况,说明以i为对称轴的回文串还没有任何一个不烦被访问过
这是我们只能从i开始向左右暴力扩展了
直到两端的字符不同,或者到达字符串边界时停止
不要忘了更新 pos 和 MaxR
空间复杂度:插入分隔符形成新串,占用了线性的空间大小;RL数组也占用线性大小的空间,因此空间复杂度是线性的
时间复杂度:对于每一个字符而言,操作只会进行一次,因此时间复杂度是O(n)
Code
虽然在分析的时候我们分成了好几种情况
但是在代码中,我们可以把以上情况进行简单的合并
注意,为了防止数组越界,我们在最两端增加一个互异特殊字符,所以算法中字符串是从1开始的
const int N=100010;
char ch[N]; //原字符串
char s[N<<1]; //转换后的字符串
int RL[N<<1];
int init()
{
int len=strlen(ch);
s[0]='@'; //字符串开头增加一个特殊字符,防止越界
for (int i=1;i<=len*2;i+=2)
{
s[i]='#';
s[i+1]=ch[i/2];
}
s[2*len+1]='#';
s[2*len+2]='$';
return 2*len+1; //返回转换字符串的长度
}
int Manacher()
{
int len=init();
int MaxR=0,ans=0,pos=0;
for (int i=1;i<=len;i++)
{
int j=2*pos-i;
if (ielse RL[i]=1; //如果i>=MaxR,要从头开始匹配
while (s[i-RL[i]]==s[i+RL[i]]) RL[i]++;
if (RL[i]+i>MaxR) { //更新pos和MaxR的值
MaxR=i+RL[i];
pos=i;
}
ans=max(ans,RL[i]);
}
return ans-1; //返回Len[i]中的最大值-1即为原串的最长回文子串额长度
}