马尔可夫决策过程(MDP)

一、强化学习引入

• 强化学习的一个经典简化图：
  
• 在上图中Agent首先观察获取当前环境的状态$S_t$,然后根据$S_t$采取一个行动$A_t$与环境进行交互，在动作$A_t$作用下环境的状态由$S_t$转变为$S_{t+1}$,同时环境会给出立即给Agent一个回报$R_t$。如此循环下去，Agent与环境进行不断地交互从而产生很多数据。强化学习算法利用产生的数据修改Agent的动作策略，再与环境交互，产生新的数据，并利用新的数据进一步改善Agent的行为，经过数次迭代学习后，智能体能最终地学到完成相应任务的最优动作。
• 在强化学习中，马尔科夫决策过程（Markov decision process, MDP）是对完全可观测的环境进行描述的，也就是说观测到的状态内容完整地决定了决策的需要的特征。几乎所有的强化学习问题都可以转化为MDP。

二、马尔科夫决策过程

• 内容大纲:
  • 马尔科夫性
  • 马尔科夫过程
  • 马尔科夫决策过程

1、马尔科夫性

• 马尔科夫性：是指环境的下一个状态$s_{t+1}$仅与当前状态$s_t$有关，而与以前的状态无关,可用下面公式表达：$$P(s_{t+1}│s_t,\dots ,s_1)=P(s_{t+1}│s_t)$$
• 马尔科夫性描述的是环境的每个状态的性质
• 马尔科夫随机过程：数学中用来描述随机变量序列的学科叫随机过程。所谓随机过程就是指随机变量序列。若将满足马尔可夫性的环境状态$s_t$视为一个随机变量，那么随机变量序列（随机过程）：$[s_1,s_2\dots ,s_n]$被称为马尔科夫随机过程

2、马尔科夫过程

• 马尔科夫过程：又叫马尔科夫链(Markov Chain)，它是一个无记忆的随机过程，可以用一个二元组$[S,P]$表示，且满足：$S\in R^N$是有限状态集合，$P\in R^{n\times n}$是状态转移概率矩阵：
  
• 例子：学生马尔科夫链：
  
  • 上图是一个马尔科夫过程示例图，状态集合$S$={娱乐,课程1,课程2,课程3,考过,睡觉,论文},状态转移概率矩阵$P$的元素为图上边的权值。
  • 一个学生一天可能的状态序列有很多种可能，比如：课1->课2->课3->考过->睡觉。这种状态序列称为马尔科夫链。当给定状态转移概率矩阵，从某个状态出发存在多条马尔科夫链。
• 但是马尔科夫过程中不存在动作(action)和奖励(reward),所有马尔科夫过程不足以描述图1所示的强化学习过程。将动作(action)和奖励(reward)考虑到马尔科夫过程中去就得到了马尔科夫决策过程。

3、马尔科夫决策过程

• 马尔科夫决策过程由元组$(S,A,P,R,\gamma )$描述其中：

  • $S\in R^n$为有限的状态集
  • $A\in R^m$为有限的动作集
  • $P\in R^{n\times m\times n}$为状态转移概率矩阵
  • $R$为回报函数
  • $\gamma$为折扣因子，用来计算累积回报。

• 跟马尔科夫过程不同的是，马尔科夫决策过程的状态转移概率是包含动作的即:$$P_{s{s}^{\prime }}^a=P[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$$表示在状态$s$下执行行为$a$下一个状态为$s^{\prime }$的概率，

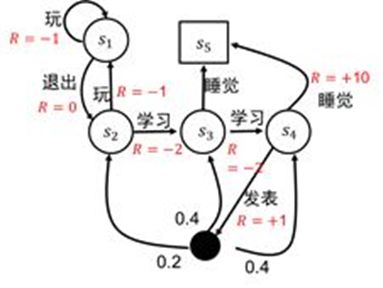
• 例子：学生马尔科夫决策过程：

  
  其中黑色源点是起点，方块为终点。
  • 该图在上图的基础上加入了行为集合$A$={完、学习、退出、睡觉、发表}和立即奖励函数$R$

• 强化学习的目标是给定一个马尔科夫决策过程，寻找最优策略。所谓策略是指状态到动作的映射，策略常用符号$\pi$表示，它是指给定状态$s$时，动作集上的一个分布，即：$$\pi (a│s)=P(A_t|S_t=s)$$

• 累计回报$G_t$:是指从$t$时刻所能带来的所有打折后的奖励总和:$$G_t=R_{t+1}+\gamma R_t+\cdots =\sum _{k=1}^{\infty }{r}^k{R}_{t+k+1}$$

  • 当给定策略$\pi$时，假设从状态$s_1$出发，学生状态序列有很多的可能：$$\begin{gathered} s_1\to s_2\to s_3\to s_4\to s_5 \\ {s}_1\to s_2\to s_3\to s_5 \\ \dots \dots \dots \dots \end{gathered}$$
  • 为了评价状态$s_1$的价值，我们需要定义一个确定量来描述状态$s_1$的价值，很自然的想法是利用累积回报来衡量状态$s_1$的价值。然而，由于策略$\pi$是随机的，因此累积回报$G_1$是个随机变量，不是一个确定值，因此无法进行描述。但其期望是个确定值，可以作为状态$s_1$的价值。每个状态的价值又被称为状态值函数。

• 状态值函数：

  • 当Agent采用策略$\pi$时，累积回报$G$服从一个分布，累积回报在状态$s$处的期望值定义为状态值函数：$$v_{\pi }(s)=E_{\pi }[\sum _k^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s]$$该式子是所有以状态$s$为起点的状态序列的累计回报的期望(概率加权和)。
  • 状态值函数是与策略$\pi$是相对应的，这是因为策略$\pi$决定了累积回报$G$的状态分布。
  • 例子：学生马尔科夫链的状态值函数示意图：
    
    节点的数字就是状态值函数

• 状态-行为值函数： $$q_{\pi }(s,a)=E_{\pi }[\sum _k^{\infty }{\gamma }^k{R}_{(}t+k+1)|S_t=s,A_t=a]$$

  • 由表示可以看出状态-行为值函数$q_{\pi }(s,a)$是在状态值函数$v_{\pi }(s)$的基础上选定一个动作$a$而得到的。

• 上面两个式子分别给出了状态值函数和状态-行为值函数的定义计算式，但在实际真正计算和编程的时候并不会按照定义式去编程。

• 状态值函数与状态-行为值函数的贝尔曼方程：

  • 状态值函数的贝尔曼方程 ：$$\begin{gathered} v(s)=E[G_t│S_t=s] \\ =E[R_{t+1}+\gamma R_{t+2}+\cdots │S_t=s] \\ =E[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+\cdots )│S_t=s] \\ =E[R_{t+1}+\gamma G_{t+1}│S_t=s] \\ =E[R_{t+1}+\gamma v(S_{t+1})|S_t=s] \end{gathered}$$最后一个等式的证明：$$\begin{gathered} v(s)=E_{s,S_{t+1}\dots }[R_{t+1}+\gamma G_{t+1}] \\ =E_{s,S_{t+1}}[R_{t+1}+\gamma E_{S_{t+1}\dots }[G_{t+1}]] \\ =E_{s,S_{t+1}}[R_{t+1}+\gamma v(S_{t+1})] \end{gathered}$$其中：$s,S_{t+1}\dots$是枚举所有的以状态$s$为起点的状态序列。$s,S_{t+1}$表示状态s到状态$S_{t+1}$的概率分布(可以直接连接为概率)。
  • 状态-动作值函数的贝尔曼方程：$$q_{\pi }(s,a)=E_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s,A_t=a]$$

• 状态值函数与状态-行为值函数的分解公式：

  • 状态值函数的计算分解示意图：
    
    其中空心点表示状态，实心点表示行为
  • 由B图可以得到：$$v_{\pi }(s)=\sum _{a\in A}\pi (a│s)q_{\pi }(s,a)$$
  • 由C图可以得到：$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })$$$R_s^a$是在状态s采取行为$a$获得的收益，$P_{s{s}^{\prime }}^a$在状态$s$采取行为$a$后状态转变为$s^{\prime }$的概率。
  • 最终状态值函数变为：$$v_{\pi }(s)=\sum _{a\in A}\pi (a│s)(R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$$
  • 状态-行为值函数的计算分解示意图:
    
  • 由图C可以得到：$$v_{\pi }(s^{\prime })=\sum _{a\in A}\pi (a^{\prime }│s^{\prime })q_{\pi }(s^{\prime },a^{\prime })$$
  • 最终得到行为状态-行为值函数：$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\sum _{a\in A}\pi (a^{\prime }│s^{\prime })q_{\pi }(s^{\prime },a^{\prime })$$

• 计算状态值函数的目的是为了构建学习算法从数据中得到最优策略。每个策略对应着一个状态值函数，最优策略自然对应着最优状态值函数;

  • 最优状态值函数$v^{\ast }(s)$为:在所有策略中值最大的状态值函数即: $$v^{\ast }(s)=ma{x}_{\pi }{v}_{\pi }(s)$$
  • 最优状态-行为值函数$q^{\ast }(s,a)$为:在所有策略中最大的状态-行为值函数，即：$$q^{\ast }(s,a)=ma{x}_{\pi }{q}_{\pi }(s,a)$$

• 最优状态值函数和最优状态-行动值函数的贝尔曼最优方程：

  • 最优状态值函数: $$v^{\ast }(s)=ma{x}_{\pi }{v}_{\pi }(s)=ma{x}_{\pi }(\sum _{a\in A}\pi (a│s)q_{\pi }(s,a))$$假设最优决策为${\pi }^{\ast }$,假设$a^{\ast }=argma{x}_a{q}_{{\pi }^{\ast }}(s,a)=argma{x}_a{q}^{\ast }(s,a)$,则要想 $v^{\ast }(s)$最大必须有：$${\pi }^{\ast }(a│s)=\{\begin{array}{ll}1& \text{if }a=a^{\ast }\\ 1& \text{if }a\ne a^{\ast }\end{array}$$这样就有：$$v^{\ast }(s)=ma{x}_a{q}^{\ast }(s,a)$$由此可知：最优状态值函数为与其相连的最优状态-行动值函数的最大值决定

  • 最优状态-行动值函数：$$\begin{gathered} q^{\ast }(s,a)=ma{x}_{\pi }{q}_{\pi }(s,a) \\ =ma{x}_{\pi }(R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })) \\ =R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^{a}ma{x}_{\pi }{v}_{\pi }(s^{\prime })=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}^{\ast }(s^{\prime }) \end{gathered}$$由此可知：最优状态-行动值函数为与其相连的最优状态值函数的概率加权和。由于：$$v^{\ast }(s^{\prime })=ma{x}_{a^{\prime }}{q}^{\ast }(s^{\prime },a^{\prime })$$所以最终最优状态-行动值函数为：$$q^{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^{a}ma{x}_a^{\prime }{q}^{\ast }(s^{\prime },a^{\prime })$$

  • 所以最终最优状态值函数为：$$\begin{gathered} v^{\ast }(s)=ma{x}_a{q}^{\ast }(s,a)=ma{x}_a(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^{a}ma{x}_{\pi }{v}_{\pi }(s^{\prime })) \\ =ma{x}_a(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}^{\ast }(s^{\prime })) \end{gathered}$$

• 例子：学生马尔科决策过程的最优值函数和最优策略如下图：

  

4、马尔可夫决策过程的形式化描述：

• 定义一个马尔科夫决策过程：$M=(S,A,P,r,{\rho }_0,\gamma ,T)$其中：
  • $S$为状态集
  • $A$为动作集
  • $P\in R^{|S|\times |A|\times |S|}$为状态概率转移矩阵
  • $r\in R^{|S|\times |A|}$为回报函数
  • $\gamma \in [0,1]$为折扣因子
  • $T$为水平范围（其实就是步数）
• 令$\tau =(s_0,a_0,s_1,a_2,\dots ,s_T,a_T)$为一个决策轨迹
• 令一个决策轨迹的累积回报为：$$R=\sum _{t=0}^T{\gamma }^t{r}_t$$
• 强化学习的目标是：找到最优策略$\pi$，使得该策略下的累积回报期望最大,即：$$ma{x}_{\pi }\sum _{\tau }R(\tau )P_{\pi }(\tau )$$

5、强化学习算法分类：

• 强化学习算法根据以策略为中心还是以值函数最优为中心可以分为两大类：
  • 策略优化方法：又分为进化算法和策略梯度方法
  • 动态规划方法：又分为策略迭代算法和值迭代算法
• 强化学习算法根据策略是否是随机的：
  • 确定性策略强化学习
  • 随机性策略强化学习
• 强化学习算法根据转移概率是否已知可以分为：
  • 基于模型的强化学习算法
  • 无模型的强化学习算法
• 根据回报函数$r∈R^{|S|×|A|}是否已知可以分为：
  • 强化学习
  • 逆向强化学习：逆向强化学习是根据专家实例将回报函数学出来

参考连接https://zhuanlan.zhihu.com/p/25498081