替罪羊树ScapeGoatTree&&(【luogu3369&&bzoj3324】普通平衡树)
先放一份代码,之后补一下。。
=====================我是萌萌哒分割线========================
扯淡
NOIP已经过去,接下来将是省选的季节,于是想要学点数据结构啊啥的涨一涨自己的姿势水平,然后忽然看到一种数据结构叫替罪羊树,感觉非常有趣,于是就点进去学了学。参考来源戳这
正文
前言
我们知道,对于一颗二叉搜索树,最重要的就是要维护他的平衡,以保证对于每次删除,插入,查询等操作均摊下来都是 O(logN) 的复杂度,不然他也就成为一颗废树了。
而对于如何维护一棵树的平衡,各种数据结构就各显神通用了各种不同的方法,但很多都是用旋转的方法来进行维护的,像Splay,Treap树等等,然而这些树都太高端了(应该是我太菜了并不会)。而这颗替罪羊树,则不需要通过旋转操作就可以维护它的平衡,在各种数据结构中非常不一样,它的思想非常简单,不平衡直接重构嘛,哪要旋转来旋转去的(233)。
重构
对于替罪羊树的重构,它的重构可以重构一整颗树,也可以重构其中的一颗子树。而对于要重构的那颗树,我们将它拍扁成一个序列,就是从小到大回收节点,就是中序遍历回收,然后重构就将最中间那个节点拿来当这个重构子树的根,然后左右分别递归下去一样做,这样就可以基本做到平衡,而一颗二叉平衡树的性质也是很显然地保证了的。
For Example:
对于这样一颗树,虽然我们还暂时不知道重构的条件是什么,但是很显然,这样的树一看就需要重构。
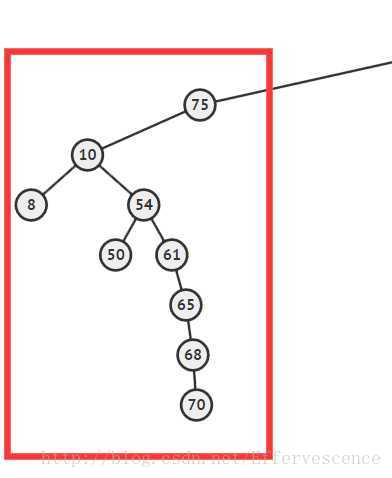
对于重构的方式,我们先 O(n) 中序遍历这颗子树,然后将所有节点回收,就成了下面这样一个序列:

然后我们用二分的方法进行递归重构,这颗子树就成了下面这样的一颗树:
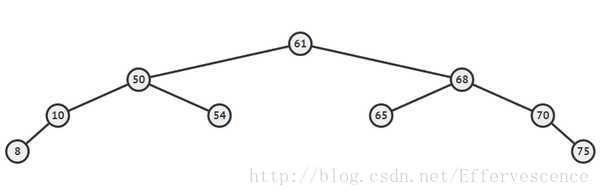
这样,我们就将这颗树重构完了,是不是看起来非常暴力啊233?没错!他就是暴力!
插入
插入部分的话,刚开始的操作跟普通平衡树差不多,直接插入就行了,只不过插入完之后需要一层一层回溯上去,查询是否有不平衡的节点,对于这里的平衡指的是对于一个节点x,定义一个 alpha(0.5<=alpha<=1) ,如果满足 size(lson(x)<=size(x)∗alpha && size(rson(x))<=size(x)∗alpha , 即两个子树的size都不超过以该节点为根的子树的size,那就称这个节点或这个子树是平衡的。我们需要向上找到第一个不平衡的点,将这整颗子树进行重构就行了,复杂度是 O(logN) 的。这里有人就有疑问了,重构复杂度不应该是 O(N) 么,怎么就是 O(logN) 的复杂度了。因为我们一次插入操作的复杂度是 O(logN) ,而我们并不是每次都要重构一棵树,且我们重构也不一定每次都是重构整颗树,所以均摊下来还是 O(logN) 的。
删除
对于删除操作,这与普通的一些平衡树不一样,我们通过找到它的左子树的最后一个节点来顶替这个被删除的节点或者它的右子树的第一个节点来顶替,这样才不会将这颗树平衡性质给破坏掉,而对于删除掉的这个节点,我们并不需要将他真正删除,只是相当于给它打一个删除标记,在查询的时候不经过它就行了。显然我们也很容易证明复杂度是 O(logN) 。
查询
而查询操作则就是普通的二叉平衡树的各种查询就行了,而这些操作的复杂度也依旧是 O(logN) 的,详细做法在代码里有解释。
例题
LuoguP3369
Bzoj3324
这两个是同一题。
/*
替罪羊树模板,题目是bzoj3324。
对于一颗不平衡的树,我们进行暴力重构将它压扁成一个序列,然后暴力重构成一颗平衡的树
这里平衡指的是对于一个节点x,定义一个alpha(0.5<=alpha<=1),
如果满足size(lson(x)<=size(x)*alpha && size(rson(x))<=size(x)*alpha,
即两个子树的size都不超过以该节点为根的子树的size,那就称这个节点或这个子树是平衡的。
P.S. alpha选太大太小都不好,最好可以选在0.75左右。
Complexity: 均摊为O(logn)。
*/
#pragma GCC optimize(3)
#include//如果现在的节点值比查询的小,那就往左走,不然往右走
}
}
inline void erase(int id) { //对一个节点进行删除操作
if(t[id].son[0]&&t[id].son[1]) {
int current=t[id].son[0];
while(t[current].son[1])
current=t[current].son[1];
t[id].num=t[current].num;
id=current;
} //删除操作需要找到左子树的最后一个节点或右子树的第一个节点来顶替,优先找左子树
int child=t[id].son[0]?t[id].son[0]:t[id].son[1],k=t[t[id].fa].son[1]==id;
t[t[t[id].fa].son[k]=child].fa=t[id].fa;
for(int i=t[id].fa;i;i=t[i].fa) //对于被删除的节点的祖先需要将它们的size减1
t[i].siz--;
if(id==root) //如果删掉的是根,则需要更新根
root=child;
}
inline int get_rank(int x) { //查询x的排名
int now=root,ans=0;
while(now) {
if(t[now].num//如果x大于现在节点的值,则需要将该节点的左子树的size与该节点加到ans里,因为左子树里的值<该节点值
ans+=t[t[now].son[0]].siz+1;
now=t[now].son[1];
}
else
now=t[now].son[0];
}
return ans;
}
inline int get_kth(int x) { //查询树中第k个数
int now=root;
while(1) {
if(t[t[now].son[0]].siz==x-1)
return now;
else if(t[t[now].son[0]].siz>=x)
now=t[now].son[0];
else { //与get_rank的这个地方差不多同一个道理(就是x的值大于当前左子树的size+1)时往右走并且减掉左子树的size+1
x-=t[t[now].son[0]].siz+1;
now=t[now].son[1];
}
}
return now;
}
inline int prev(int x) { //找前驱,即左子树中的最后一个点
int now=root,ans=-oo;
while(now) {
if(t[now].num1];
}
else
now=t[now].son[0];
}
return ans;
}
inline int succ(int x) { //找后继,即右子树中的第一个点
int now=root,ans=oo;
while(now) {
if(t[now].num>x) {
ans=min(ans,t[now].num);
now=t[now].son[0];
}
else
now=t[now].son[1];
}
return ans;
}
inline void init() { //初始化
cntx=2;root=1;
t[1].num=-oo,t[1].siz=2,t[1].son[1]=2;
t[2].num=oo,t[2].siz=1,t[2].fa=1;
}
inline void main() {
init();
read(n);
while(n--) {
int op,x;
read(op);read(x);
if(op==1)
insert(x);
if(op==2)
erase(get_num(x));
if(op==3)
writeln(get_rank(x));
if(op==4)
writeln(t[get_kth(x+1)].num);
if(op==5)
writeln(prev(x));
if(op==6)
writeln(succ(x));
}
}
}SGT;
int main() {
SGT.main();
return 0;
}