LeetCode 785. 判断二分图

目录结构

1.题目

2.题解

2.1DFS

2.2BFS

---

1.题目

给定一个无向图graph，当这个图为二分图时返回true。

如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合，一个来自B集合，我们就将这个图称为二分图。

graph将会以邻接表方式给出，graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边： graph[i] 中不存在i，并且graph[i]中没有重复的值。

示例：

输入: [[1,3], [0,2], [1,3], [0,2]]
输出: true
解释: 
无向图如下:
0----1
|    |
|    |
3----2
我们可以将节点分成两组: {0, 2} 和 {1, 3}。



入: [[1,2,3], [0,2], [0,1,3], [0,2]]
输出: false
解释: 
无向图如下:
0----1
| \  |
|  \ |
3----2
我们不能将节点分割成两个独立的子集。

注意:

• graph 的长度范围为 [1, 100]。
• graph[i] 中的元素的范围为 [0, graph.length - 1]。
• graph[i] 不会包含 i 或者有重复的值。
• 图是无向的: 如果j 在 graph[i]里边, 那么 i 也会在 graph[j]里边。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/is-graph-bipartite
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.题解

2.1DFS

• 对节点进行DFS，并交替标记：0、1、2分别表示未访问、属于集合1、属于集合2。
• 一旦不满足条件则返回false，否则遍历结束返回true。

public class Solution785 {

    @Test
    public void test785() {
        int[][] graph = {{1, 2, 3}, {0, 2}, {0, 1, 3}, {0, 2}};
        System.out.println(isBipartite(graph));
    }

    //0、1、2分别表示未访问、属于集合1、属于集合2
    public int[] visFlag;
    public boolean flag;

    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        visFlag = new int[n];
        flag = true;
        for (int i = 0; i < n && flag; i++) {
            if (visFlag[i] == 0) {
                dfs(i, 1, graph);
            }
        }
        return flag;
    }

    public void dfs(int node, int sign, int[][] graph) {
        visFlag[node] = sign;
        sign = sign == 1 ? 2 : 1;
        for (int neighbor : graph[node]) {
            if (visFlag[neighbor] == 0) {
                dfs(neighbor,sign,graph);
                if (!flag){
                    return;
                }
            } else if(visFlag[neighbor] != sign){
                flag = false;
                return;
            }
        }
    }
}

• 时间复杂度：
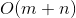
• 空间复杂度：

2.2BFS

• 对节点进行BFS，并交替标记：0、1、2分别表示未访问、属于集合1、属于集合2。
• 一旦不满足条件则返回false，否则遍历结束返回true。

public class Solution785 {

    @Test
    public void test785() {
        int[][] graph = {{1, 2, 3}, {0, 2}, {0, 1, 3}, {0, 2}};
        System.out.println(isBipartite(graph));
    }

    //0、1、2分别表示未访问、属于集合1、属于集合2
    public int[] visFlag;
    public boolean flag;

    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        visFlag = new int[n];
        flag = true;
        bfs(n,graph);
        return flag;
    }

    public void bfs(int n,int[][] graph){
        for (int i = 0; i < n; ++i) {
            if (visFlag[i] == 0) {
                Queue queue = new LinkedList<>();
                queue.offer(i);
                visFlag[i] = 1;
                while (!queue.isEmpty()) {
                    int node = queue.poll();
                    int sign = visFlag[node] == 1 ? 2 : 1;
                    for (int neighbor : graph[node]) {
                        if (visFlag[neighbor] == 0) {
                            queue.offer(neighbor);
                            visFlag[neighbor] = sign;
                        } else if (visFlag[neighbor] != sign) {
                            flag = false;
                            return;
                        }
                    }
                }
            }
        }
    }
}

• 时间复杂度：
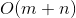
• 空间复杂度：