各种背包问题原理，例题，代码实现

1. 0/1背包

1.1 问题描述

一个旅行者有一个容量为V的背包，现在有N件物品，它们的价值分别是 W1 ，W2 ，… , Wn ,它们所要占用的容量分别为 C1，C2 ，… ，Cn 。若每种物品只有一件求旅行者能获得最大总价值。

1.2 基本思路

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。
用子问题定义状态：即 F [i; j] 表示前 i 件物品恰放入一个容量为 j 的背包可以获得的最大价值。则其状态转移方程便是：

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：“将前 i 件物品放入容量为 v 的背包中”这个子问题，若只考虑第 i 件物品的策略（放或不放），那么就可以转化为一个只和前 i − 1 件物品相关的问题。如果不放第 i 件物品，那么问题就转化为“前 i − 1 件物品放入容量为 v 的背包中”，价值为 F [i − 1; v]；如果放第 i 件物品，那么问题就转化为“前 i − 1 件物品放入剩下的容量为v − Ci的背包中”，此时能获得的最大价值就是 F [i − 1; v − Ci] 再加上通过放入第 i 件物品获得的价值 Wi。

1.3 例题

设包的容量为8， 物品数量为4，每件物品的体积和价值如下所示：

编号	1	2	3	4
体积	2	3	4	5
价值	3	4	5	6

求所能获取的最大价值。
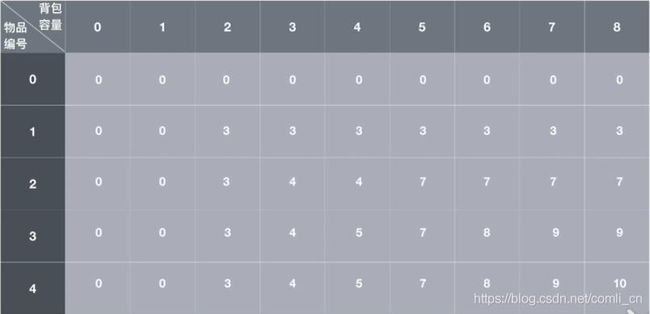（1）表格里填的数字是在当前背包容量为$j$的情况下有选择地放前$i$个物品所能得到的最大价值。

（2）先给第0行和第0列填上0，因为第0行代表放前0个物品，最大价值必然为0；第0列代表背包容量为0，最大价值也必然为0

（3）剩余的空格按照如下规则进行计算：
a.两层循环，先对物品数量进行遍历，然后对背包容量进行遍历
b.在背包容量为$j$的情况下能否将第$i$个物品放进去；
c.如果能的话将第$i$个物品的价值加到这个空格里面，然后计算剩余背包容量，看一下剩余背包容量在前$i-1$个物品存放时能获取的最大值与第$i$个物品的价值相加放入空格里面；
d.如果不能的话将背包容量为$j-1$的情况下放前$i-1$个物品所能获得的最大价值填在$j,i$这个空格里面
e.当背包容量可以将当前物品全部放进去时，在当前物品数量的情况下对背包容量的后续遍历所能填的值将不会再改变了；

举例

我们假设用F来代表这个表格：

则F[1][2]=3,这是因为背包容量为2的情况下只能把第一个物品放进去，价值为3；

F[2][3]=4，这是因为容量为3的情况下首先考虑能否把编号为2的物品放进去，可以放进去，但因为编号为2的物品体积为3，故只能放它一个，此时价值为4，如果不放编号为2的物品则最大值为F[1][3]=3,两相比较选择把编号为2的物品放进去；

F[3][6]=8,这是因为在容量为6的情况下先考虑能否把编号为3的物品放进去，可以，且因为编号为3的物品体积为4，故6-4=2，还有2的容量可以放其他东西，这个时候跳到F[2][2]，即在剩余容量为2的情况下放前两个物品最多可以获取多少价值，F[2][2]=3，故F[3][6]=5+F[2][2]=8 (编号为3的物品价值为5)。

以上所举几个例子就可以印证式子：

1.4 代码

def packetProblem(V, N, volume_list, value_list):
    F = [[0 for i in range(V+1)] for j in range(N+1)]
    for i in range(1, N+1):
        for j in range(1, V+1):
            if j >= volume_list[i-1]:  # 当前背包容量能否装下编号为i的物品
                F[i][j] = max(F[i-1][j], F[i-1][j-volume_list[i-1]]+value_list[i-1])
            else:
                F[i][j] = F[i-1][j]
    return F[-1][-1]


V = 8
N = 4
volume_list = [2, 3, 4, 5]
value_list = [3, 4, 5, 6]
result = packetProblem(V, N, volume_list, value_list)
print(result)

结果：

10

1.5 算法改进

因为从0/1背包问题的动态规划式子中可以看到F[i][j]的值只与上一行的F[i]的值有关，所以可以使用滚动数组的方式，只定义一个一维的F数组然后每次对这个数组进行更新。即可将下面的式子：

改为：

1.6 改进后的代码

第二个循环一定要从后往前推

def packetProblem(V, N, volume_list, value_list):
    F = [0 for i in range(V+1)]
    for i in range(1, N+1):
        for j in range(V, 0, -1):  ## 这里要从后往前推
            if j >= volume_list[i-1]:  # 当前背包容量能否装下编号为i的物品
                F[j] = max(F[j], F[j-volume_list[i-1]]+value_list[i-1])
    return F[-1]

1.7. 0/1背包回溯

1.7.1 问题描述

一个旅行者有一个容量为V的背包，现在有N件物品，它们的价值分别是 W1 ，W2 ，… , Wn ,它们所要占用的容量分别为 C1，C2 ，… ，Cn 。若每种物品只有一件求旅行者怎样选择物品才能获得最大总价值。

1.7.2 基本思路

在已经求出0/1背包问题的前提下，我们已经得到了一个如下的表格，接下来就从这个表格的右下角开始往回推理：

编号	1	2	3	4
体积	2	3	4	5
价值	3	4	5	6

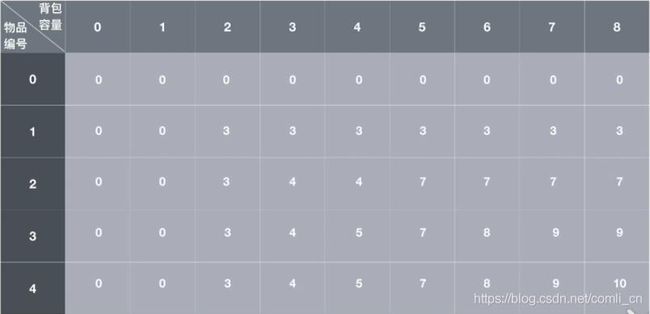
当背包容量为8，装4个物品的时候最优，即F[4][8]=10，然后看到背包容量为8装3个物品的时候F[3][8]最优为9，说明最终编号为4的物品是放进了背包里面的，所以用现在的容量减去编号为4的物体的体积8-5=3，剩余容量为3,看前3个物品；F[3][3]=4， F[2][3]=4,说明编号为3的物品没有放进背包里；然后看F[2][3] =4,F[1][3]=3说明编号为2的物品放进了背包里,剩余容量为3-3=0；综上背包里放的是编号为2和4的两个物品。

2. 完全背包问题

1.1 问题描述

一个旅行者有一个容量为V的背包，现在有N件物品，它们的价值分别是 W1 ，W2 ，… , Wn ,它们所要占用的容量分别为 C1，C2 ，… ，Cn 。若每种物品可以取任意件求旅行者能获得最大总价值。

1.2 一个朴素的思路

可以在0/1背包问题的基础上加上一层代表选取了k个相同物品的循环，而k的最大值由背包容量除以每件物品的体积来求得。

代码：

### 完全背包问题

def packetProblem(V, N, volume_list, value_list):
    F = [0 for i in range(V+1)]
    for i in range(1, N+1):
        for j in range(V, 0, -1):
            for k in range(0, j//volume_list[i-1]+1):
                if j >= volume_list[i-1]:  # 当前背包容量能否装下编号为i的物品
                    F[j] = max(F[j], F[j-k*volume_list[i-1]]+k*value_list[i-1])
    return F[-1]


V = 8
N = 4
volume_list = [2, 3, 4, 5]
value_list = [3, 4, 5, 6]
result = packetProblem(V, N, volume_list, value_list)
print(result)

结果为：

12

1.3 终极解法

0/1背包问题的表格及动态规划方程(w是物品的体积，C是物品的价值)：

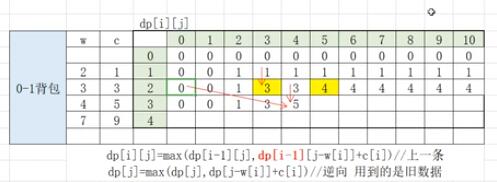
完全背包问题的表格及动态规划方程：

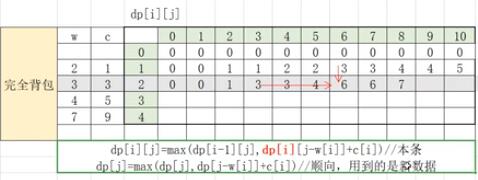
可以看到dp[1][4]=2,这是因为此时可以放两个编号为1的物品；再看dp[2][6]=6,过程是先往容量为6的背包里放体积为3的物品，因为可以放任意个，所以dp[2][6]-3=dp[2][3],也就是说不再往它的前一行看了，而是往本行的前面看。两个问题进行一维简化后的式子是一样的，唯一不同在于第二个循环0/1背包问题是逆向的，而完全背包问题是顺向的。

def packetProblem(V, N, volume_list, value_list):
    F = [0 for i in range(V+1)]
    for i in range(1, N+1):
        for j in range(volume_list[i-1], V+1):
            F[j] = max(F[j], F[j-volume_list[i-1]]+value_list[i-1])
    return F[-1]


V = 8
N = 4
volume_list = [2, 3, 4, 5]
value_list = [3, 4, 5, 6]
result = packetProblem(V, N, volume_list, value_list)
print(result)

3. 完全背包问题的变种

3.1 问题描述

给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。(结果可能会很大，你需要将结果模上1000000007)。

3.2 示例

示例1:

输入: n = 5
输出：2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1

示例2:

输入: n = 10
输出：4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1

来源：力扣（LeetCode）

3.3 思路

在每一步只要考虑要不要将当前这个币值的硬币放进去，要放几个，放进去之后剩余的空间和前面一个币值可以组成的方式是已知的，故只要相加即可。

3.4 过程

初始设置：

计算之后的：

如上表所示，这里关键是设第0行为0和第0列为1，这是因为n=0的话不管前几个币值都只有这一种组成方法，然后每一行只要考虑要不要将当前这个币值的硬币放进去，要放几个，放进去之后剩余的空间和前面一个币值可以组成的方式是已知的，故只要相加即可。
比如dp[2][10],如果将里面放入0个币值为5的硬币则这个空格里面的组成种类和dp[1][10]相同，如果放入1个5分，则与dp[1][5]相同，如果放入2个5分则与dp[1][0]相同。

故dp[2][10]=dp[1][10]+dp[1][5]+dp[1][0]

从而

"[]"为取整符。

代码：

def waysToChange(n):
    c = [0, 25, 10, 5, 1]
    dp = [[0]*(n+1) for _ in range(5)]
    for i in range(5):
        dp[i][0] = 1
    for i in range(1, 5):
        for j in range(1, n+1):
            for k in range(j//c[i]+1):
                dp[i][j] += dp[i-1][j-k*c[i]]
    print(dp)
    return dp[-1][-1]


result = waysToChange(11)
print(result)

结果：

4

3.5 改进

（1）优化时间复杂度

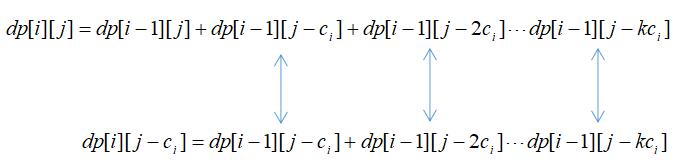
箭头两端是一样的，故动态规划式子可以转换为：

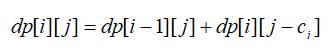
（2）优化空间复杂度
将二维列表变为一维列表：

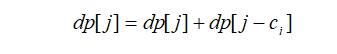
代码：

def waysToChange(n):
    c = [0, 25, 10, 5, 1]
    dp = [1] + [0]*n
    for i in range(1, 5):
        for j in range(c[i], n+1):
            dp[j] += dp[j-c[i]]
    return dp[-1]

result = waysToChange(11)
print(result)

结果：

4