深度学习论文笔记(增量学习)——CVPR2020:Mnemonics Training: Multi-Class Incremental Learning without Forgetting
文章目录
- 前言
- 工作流程
- exemplar level
前言
目前也写了较多增量学习的文章了,我的目的是在写的过程中对方法的细节进行梳理,帮助自己理解,其中难免有表述不当的地方,请各位辩证看待我文章中的观点与描述,如有错误,还望指出。
本篇文章发表于2020年CVPR,论文代码地址
作者从一个非常有趣的点出发,从而让模型抵抗灾难性遗忘,但是这篇文章细节部分写的不是很好。现有的增量学习算法多数都会存储部分旧图片,作者将旧图片作为优化参数,通过优化旧图片从而让旧图片尽可能反映旧类别的特性,最终让模型尽可能较少的遗忘。作者通过让保存的旧图片训练出的模型,在全部训练图片上计算出的loss值尽可能小,从而让旧图片尽可能反映旧类别的特性。上述方法称为Mnemonics
从exemplar level抵抗灾难性遗忘的做法,NIPS2019上也有一篇文章:Online Continual Learning with Maximally Interfered Retrieval。
先上一张简单的效果图:
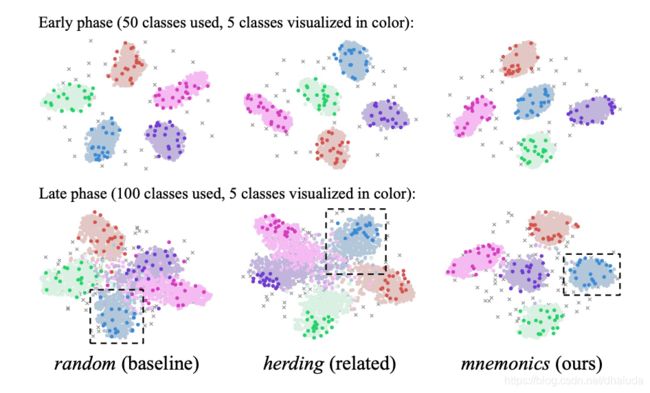
通过t-SNE技术,将高维特征映射到低维度进行可视化,结果如上,深色的点表示exemplar。可以看到,利用Mnemonics训练的model,会将类别分的更开,并且利用Mnemonics得到的旧图片,会更位于类别边缘(这个特性不知道可以说明什么)。
工作流程

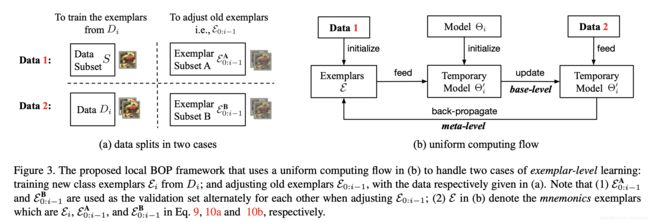
一次增量学习分为model-level与exemplar-level两个层级。model level利用蒸馏loss,结合存储的exemplar,对model进行训练,由于是增量学习的常见方法,故在此不做过多介绍。 exemplar level将对旧图片进行优化。
exemplar level
设第 i i i次增量学习后,模型的参数为 θ i \theta_i θi,对于第 i i i次增量学习的数据,作者会将其分为验证集与训练集两类,设训练集中待优化的图片为 ϵ i \epsilon_i ϵi,对应的验证集中的图片为 D i D_i Di, L c L_c Lc为交叉熵损失函数,则优化目标为
min ϵ i L c ( θ i ′ ( ϵ i ) ; D i ) s . t . θ i ′ ( ϵ i ) = arg min θ i L c ( θ i ; ϵ i ) (式1.0) \begin{aligned} &\min_{\epsilon_i}L_c(\theta'_i(\epsilon_i);D_i)\\ &s.t. \theta'_i(\epsilon_i)=\argmin_{\theta_i}L_c(\theta_i;\epsilon_i) \end{aligned}\tag{式1.0} ϵiminLc(θi′(ϵi);Di)s.t.θi′(ϵi)=θiargminLc(θi;ϵi)(式1.0)
exemplar level分为两个阶段,首先利用 θ i \theta_i θi初始化另外一个model,接着利用 ϵ i \epsilon_i ϵi训练该model,使得 L c L_c Lc取值最小,得到模型 θ i ′ ( ϵ i ) \theta'_i(\epsilon_i) θi′(ϵi),梯度更新的式子如2.0所示:
θ i ′ = θ i ′ − α Δ θ i ′ L c ( θ i ; ϵ i ) (式2.0) \theta_i'=\theta_i'-\alpha\Delta_{\theta_i'}L_c(\theta_i;\epsilon_i)\tag{式2.0} θi′=θi′−αΔθi′Lc(θi;ϵi)(式2.0)
接着固定 θ i ′ ( ϵ i ) \theta'_i(\epsilon_i) θi′(ϵi),将 ϵ i \epsilon_i ϵi作为参数进行优化,梯度更新的式子如3.0所示:
ϵ i = ϵ i − β Δ ϵ L c ( θ i ′ ( ϵ i ) ; D i ) (式3.0) \epsilon_i=\epsilon_i-\beta \Delta_{\epsilon} L_c(\theta'_i(\epsilon_i);D_i)\tag{式3.0} ϵi=ϵi−βΔϵLc(θi′(ϵi);Di)(式3.0)
L c ( θ i ′ ( ϵ i ) ; D i ) L_c(\theta'_i(\epsilon_i);D_i) Lc(θi′(ϵi);Di)表示模型 θ i ′ ( ϵ i ) \theta'_i(\epsilon_i) θi′(ϵi)在数据集 D i D_i Di上的交叉熵损失函数,模型的输入是数据集 D i D_i Di,那如何将误差反向传播至 ϵ i \epsilon_i ϵi?关于如何更新 ϵ \epsilon ϵ,作者写的不是很清楚,我这边给出自己的理解,可能是联合式2.0与式1.0进行更新,梯度反向传播至参数 θ i ′ \theta_i' θi′上后,依据式1.0,将梯度传播至 ϵ i \epsilon_i ϵi
对于旧数据,设旧数据为 ϵ 0 : i − 1 \epsilon_{0:i-1} ϵ0:i−1,作者也将其分为不相交的两部分: ϵ 0 : i − 1 A \epsilon_{0:i-1}^A ϵ0:i−1A、 ϵ 0 : i − 1 B \epsilon_{0:i-1}^B ϵ0:i−1B,将其中一部分作为验证集,优化另外一部分,通过交替优化,使得 ϵ 0 : i − 1 A \epsilon_{0:i-1}^A ϵ0:i−1A、 ϵ 0 : i − 1 B \epsilon_{0:i-1}^B ϵ0:i−1B都可以得到优化。
比如首先将 ϵ 0 : i − 1 A \epsilon_{0:i-1}^A ϵ0:i−1A作为训练集, ϵ 0 : i − 1 B \epsilon_{0:i-1}^B ϵ0:i−1B作为验证集,利用下式对 ϵ 0 : i − 1 A \epsilon_{0:i-1}^A ϵ0:i−1A进行优化
ϵ 0 : i − 1 A = ϵ 0 : i − 1 A − β Δ ϵ 0 : i − 1 A L c ( θ i ′ ( ϵ 0 : i − 1 A ) ; ϵ 0 : i − 1 B ) \epsilon_{0:i-1}^A=\epsilon_{0:i-1}^A-\beta\Delta_{\epsilon_{0:i-1}^A}L_c(\theta_i'(\epsilon_{0:i-1}^A);\epsilon_{0:i-1}^B) ϵ0:i−1A=ϵ0:i−1A−βΔϵ0:i−1ALc(θi′(ϵ0:i−1A);ϵ0:i−1B)
接着将 ϵ 0 : i − 1 B \epsilon_{0:i-1}^B ϵ0:i−1B作为训练集, ϵ 0 : i − 1 A \epsilon_{0:i-1}^A ϵ0:i−1A作为验证集,利用下式对 ϵ 0 : i − 1 B \epsilon_{0:i-1}^B ϵ0:i−1B进行优化
ϵ 0 : i − 1 B = ϵ 0 : i − 1 B − β Δ ϵ 0 : i − 1 B L c ( θ i ′ ( ϵ 0 : i − 1 B ) ; ϵ 0 : i − 1 A ) \epsilon_{0:i-1}^B=\epsilon_{0:i-1}^B-\beta\Delta_{\epsilon_{0:i-1}^B}L_c(\theta_i'(\epsilon_{0:i-1}^B);\epsilon_{0:i-1}^A) ϵ0:i−1B=ϵ0:i−1B−βΔϵ0:i−1BLc(θi′(ϵ0:i−1B);ϵ0:i−1A)
重复上述过程。
我们可以看到,式1.0的优化分为两个部分,优化模型时,图像 ϵ \epsilon ϵ固定,优化图像 ϵ \epsilon ϵ时,模型固定,这就相当于坐标下降法。优化的最终目的是使使用图像 ϵ \epsilon ϵ训练出来的model,在全部训练数据上的loss最小,即拟合全部训练数据,这样,我们在存储图像上训练出的model,和使用全部训练数据训练得到的model,性能将尽可能接近。