深度学习系列4:深度神经网络(DNN),夜空中最亮的星
引言
深度学习(DNN) 功能之强、应用之广,可以说是机器学习里最亮的星。
其实深度学习就是深度神经网络(Deep Neural Networks),也就是层次比较多的神经网络,今天我们一起来会会它。
一、深度神经网络概述
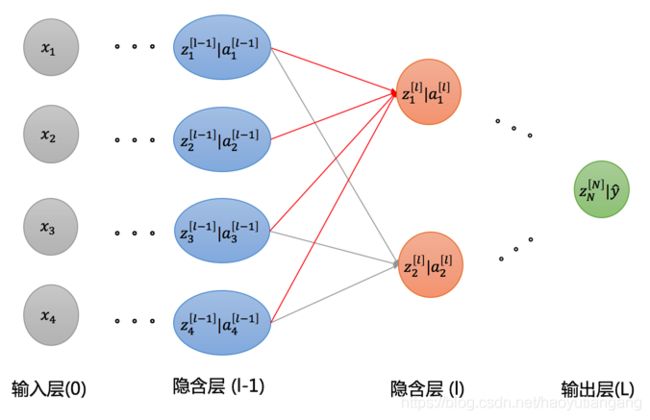
深度神经网络包括输入层、多个隐含层和输出层,每层含有多个节点。
每个节点都是一个算法神经元,从上层接收多个输入,按权重加和再用激活函数生成输出,而这个输出又作为下一层的输入。
层次多了网络就更复杂,也就可以学习到更复杂的函数关系。实验表明,只要有足够数量和维度的样本,深度学习总能学习到比较好的结果。
下面我们详细认识一下。
二、深度神经网络的表示
一般说 N 层神经网络,这里的 N 不包括输入层,仅包含隐含层和输出层。
2.1 深度神经网络的索引符号
在深度神经网络中,因为涉及到第几层第几个节点第几个样本,所以要用不同的索引来区分。拿第 l 层的第 i 个节点举例:
z i [ l ] = w [ l ] a [ l − 1 ] + b l a i [ l ] = r e l u ( z i [ l ] ) \begin{aligned} z_i^{[l]} &= w^{[l]}a^{[l-1]} + b^{{l}} \\ a_i^{[l]} &= relu(z_i^{[l]}) \end{aligned} zi[l]ai[l]=w[l]a[l−1]+bl=relu(zi[l])
- 上标中括号表示第几层: a [ 1 ] a^{[1]} a[1], a [ 2 ] a^{[2]} a[2]
- a [ l ] a^{[l]} a[l] 表示第 l 层的输出,同时也是第 l+1 层的输入
- 输入层也称为第0层,可以写成 a [ 0 ] a^{[0]} a[0]
- 输出层 y ^ \hat y y^ : 也就是最后一层的输出,表示为 a [ L ] a^{[L]} a[L]
- 上标小括号表示第几个样本: a ( 1 ) a^{(1)} a(1), a ( 2 ) a^{(2)} a(2)
- 下标表示当前层第几个节点(维度): a 1 a_1 a1, a 2 a_2 a2
2.2 深度神经网络矩阵化
如图所示,不失一般性,我们推导一下如何从 [l-1] 层 到达 [l] 层
- 第 l-1 层有四个节点(维度)
- ( a 1 [ l − 1 ] , a 2 [ l − 1 ] , a 3 [ l − 1 ] , a 4 [ l − 1 ] ) (a^{[l-1]}_1,a^{[l-1]}_2,a^{[l-1]}_3,a^{[l-1]}_4) (a1[l−1],a2[l−1],a3[l−1],a4[l−1])
- 第 l 层的有两个节点(维度)
- ( a 1 [ l ] , a 2 [ l ] (a^{[l]}_1,a^{[l]}_2 (a1[l],a2[l])
先考虑一个样本的情况
z 1 [ l ] = [ w 11 [ l ] w 12 [ l ] w 13 [ l ] w 14 [ l ] ] [ a 1 [ l − 1 ] a 2 [ l − 1 ] a 3 [ l − 1 ] a 4 [ l − 1 ] ] + b 1 [ l ] z^{[l]}_1 = \begin{bmatrix}w^{[l]}_{11}\;w^{[l]}_{12}\;w^{[l]}_{13}\;w^{[l]}_{14}\end{bmatrix} \begin{bmatrix}a^{[l-1]}_{1} \\ a^{[l-1]}_{2} \\ a^{[l-1]}_{3} \\ a^{[l-1]}_{4}\end{bmatrix} + b^{[l]}_1 z1[l]=[w11[l]w12[l]w13[l]w14[l]]⎣⎢⎢⎢⎡a1[l−1]a2[l−1]a3[l−1]a4[l−1]⎦⎥⎥⎥⎤+b1[l]
z 2 [ l ] = [ w 21 [ l ] w 22 [ l ] w 23 [ l ] w 24 [ l ] ] [ a 1 [ l − 1 ] a 2 [ l − 1 ] a 3 [ l − 1 ] a 4 [ l − 1 ] ] + b 2 [ l ] z^{[l]}_2 = \begin{bmatrix}w^{[l]}_{21}\;w^{[l]}_{22}\;w^{[l]}_{23}\;w^{[l]}_{24}\end{bmatrix} \begin{bmatrix}a^{[l-1]}_{1} \\ a^{[l-1]}_{2} \\ a^{[l-1]}_{3} \\ a^{[l-1]}_{4}\end{bmatrix} + b^{[l]}_2 z2[l]=[w21[l]w22[l]w23[l]w24[l]]⎣⎢⎢⎢⎡a1[l−1]a2[l−1]a3[l−1]a4[l−1]⎦⎥⎥⎥⎤+b2[l]
将两个公式合为矩阵:
[ z 1 [ l ] z 2 [ l ] ] = [ w 11 [ l ] w 12 [ l ] w 13 [ l ] w 14 [ l ] w 21 [ l ] w 22 [ l ] w 23 [ l ] w 24 [ l ] ] [ a 1 [ l − 1 ] a 2 [ l − 1 ] a 3 [ l − 1 ] a 4 [ l − 1 ] ] + [ b 1 [ l ] b 2 [ l ] ] \begin{bmatrix}z^{[l]}_1 \\ z^{[l]}_2\end{bmatrix}= \begin{bmatrix}w^{[l]}_{11}\;w^{[l]}_{12}\;w^{[l]}_{13}\;w^{[l]}_{14} \\ w^{[l]}_{21}\;w^{[l]}_{22}\;w^{[l]}_{23}\;w^{[l]}_{24}\end{bmatrix} \begin{bmatrix}a^{[l-1]}_{1} \\ a^{[l-1]}_{2} \\ a^{[l-1]}_{3} \\ a^{[l-1]}_{4}\end{bmatrix} + \begin{bmatrix} b^{[l]}_1 \\ b^{[l]}_2 \end{bmatrix} [z1[l]z2[l]]=[w11[l]w12[l]w13[l]w14[l]w21[l]w22[l]w23[l]w24[l]]⎣⎢⎢⎢⎡a1[l−1]a2[l−1]a3[l−1]a4[l−1]⎦⎥⎥⎥⎤+[b1[l]b2[l]]
再考虑 m 个样本的情况:
[ z 11 [ l ] … z 1 m [ l ] z 21 [ l ] … z 2 m [ l ] ] = [ w 11 [ l ] w 12 [ l ] w 13 [ l ] w 14 [ l ] w 21 [ l ] w 22 [ l ] w 23 [ l ] w 24 [ l ] ] [ a 11 [ l − 1 ] … a 1 m [ l − 1 ] a 21 [ l − 1 ] … a 2 m [ l − 1 ] a 31 [ l − 1 ] … a 3 m [ l − 1 ] a 41 [ l − 1 ] … a 4 m [ l − 1 ] ] + [ b 1 [ l ] b 2 [ l ] ] \begin{bmatrix}z^{[l]}_{11} \dots z^{[l]}_{1m}\\ z^{[l]}_{21} \dots z^{[l]}_{2m}\end{bmatrix}= \begin{bmatrix}w^{[l]}_{11}\;w^{[l]}_{12}\;w^{[l]}_{13}\;w^{[l]}_{14} \\ w^{[l]}_{21}\;w^{[l]}_{22}\;w^{[l]}_{23}\;w^{[l]}_{24}\end{bmatrix} \begin{bmatrix}a^{[l-1]}_{11} \dots a^{[l-1]}_{1m}\\ a^{[l-1]}_{21} \dots a^{[l-1]}_{2m} \\ a^{[l-1]}_{31} \dots a^{[l-1]}_{3m} \\ a^{[l-1]}_{41} \dots a^{[l-1]}_{4m}\end{bmatrix} + \begin{bmatrix} b^{[l]}_1 \\ b^{[l]}_2 \end{bmatrix} [z11[l]…z1m[l]z21[l]…z2m[l]]=[w11[l]w12[l]w13[l]w14[l]w21[l]w22[l]w23[l]w24[l]]⎣⎢⎢⎢⎡a11[l−1]…a1m[l−1]a21[l−1]…a2m[l−1]a31[l−1]…a3m[l−1]a41[l−1]…a4m[l−1]⎦⎥⎥⎥⎤+[b1[l]b2[l]]
矩阵简化为
Z 2 ∗ m [ l ] = W 2 ∗ 4 [ l ] ∗ A 4 ∗ m [ l − 1 ] + b 2 ∗ 1 [ l ] Z^{[l]}_{2*m} = W^{[l]}_{2*4} * A^{[l-1]}_{4*m} + b^{[l]}_{2*1} Z2∗m[l]=W2∗4[l]∗A4∗m[l−1]+b2∗1[l]
最后一般化,把 [l-1] 层的维度由 4 改成 l-1,[l] 层的维度由 2 改成 l, 矩阵为
Z l ∗ m [ l ] = W l ∗ l − 1 [ l ] ∗ A l − 1 ∗ m [ l − 1 ] + b l ∗ 1 [ l ] A l ∗ m [ l ] = Z l ∗ m [ l ] \begin{aligned} Z^{[l]}_{l*m} &= W^{[l]}_{l*l-1} * A^{[l-1]}_{l-1*m} + b^{[l]}_{l*1} \\ A^{[l]}_{l*m} &= Z^{[l]}_{l*m} \end{aligned} Zl∗m[l]Al∗m[l]=Wl∗l−1[l]∗Al−1∗m[l−1]+bl∗1[l]=Zl∗m[l]
总结一下:
- 输入矩阵 A l − 1 ∗ m [ l − 1 ] A^{[l-1]}_{l-1*m} Al−1∗m[l−1]: l-1 行表示第 [l-1] 层的节点(维度)数,m 列表示样本个数
- 参数矩阵 W l ∗ l − 1 [ l ] W^{[l]}_{l*l-1} Wl∗l−1[l]: l 行表示第 [l] 层的节点(维度)数,l-1 列表示第 [l-1] 层的节点(维度)数
- 参数向量 b l ∗ 1 [ l ] b^{[l]}_{l*1} bl∗1[l]: l 行表示第 [l] 层的节点(维度)数,1 列表示列向量,计算时维度自适应
- 输出矩阵 Z l ∗ m [ l ] Z^{[l]}_{l*m} Zl∗m[l]: l 行表示第 [l] 层的节点(维度)数,m 列表示样本个数
- 激活矩阵 A l ∗ m [ l ] A^{[l]}_{l*m} Al∗m[l]: 维度与 Z 一致。既是上一层的输出,同时也是下一层的输入
三、求解深度神经网络
神经网络的求解仍然采用梯度下降的方法。
3.1 正向传播
层次:{1, …, l-1, l, …, L}
- 隐含层
Z [ 1 ] = W [ 1 ] ∗ X + b [ 1 ] A [ 1 ] = g [ 1 ] ( Z [ 1 ] ) \begin{aligned} Z^{[1]} &= W^{[1]} * X + b^{[1]} \\ A^{[1]} &= g^{[1]}(Z^{[1]}) \end{aligned} Z[1]A[1]=W[1]∗X+b[1]=g[1](Z[1])
。。。
Z [ l ] = W [ l ] ∗ A [ l − 1 ] + b [ l ] A [ l ] = g [ l ] ( Z [ l ] ) \begin{aligned} Z^{[l]} &= W^{[l]} * A^{[l-1]} + b^{[l]} \\ A^{[l]} &= g^{[l]}(Z^{[l]}) \end{aligned} Z[l]A[l]=W[l]∗A[l−1]+b[l]=g[l](Z[l])
。。。 - 输出层
Z [ L ] = W [ L ] ∗ A [ L − 1 ] + b [ L ] Y ^ = A [ L ] = g [ L ] ( Z [ L ] ) \begin{aligned} Z^{[L]} &= W^{[L]} * A^{[L-1]} + b^{[L]} \\ \hat Y &= A^{[L]} = g^{[L]}(Z^{[L]}) \end{aligned} Z[L]Y^=W[L]∗A[L−1]+b[L]=A[L]=g[L](Z[L]) - 损失函数
a. 回归时
L o s s = 1 2 ( A − Y ) 2 Loss = \frac12(A - Y)^2 Loss=21(A−Y)2
b. 二分类时
L o s s = − ( Y ln A + ( 1 − Y ) ln ( 1 − A ) ) Loss = -(Y\,\ln A + (1-Y)\,\ln (1-A) ) Loss=−(YlnA+(1−Y)ln(1−A))
c. 多分类时
L o s s = − ∑ j Y j ln A j Loss = -\sum_j Y_j \ln A_j Loss=−j∑YjlnAj
其中 g [ l ] g^{[l]} g[l] 表示第 l 层的激活函数,通常隐含层采用relu,输出层采用sigmoid(二分类)或者softmax(多分类)。
3.2 反向传播
反向传播中主要利用链式求导法则,即 ∂ z ∂ x = ∂ z ∂ y ∂ y ∂ x \frac{\partial z}{\partial x} = \frac{\partial z}{\partial y}\,\frac{\partial y}{\partial x} ∂x∂z=∂y∂z∂x∂y
-
输出层
d Z [ L ] = A [ L ] − Y d W [ L ] = 1 m d Z [ L ] A [ L − 1 ] T d b [ L ] = 1 m s u m ( d Z [ L ] ) \begin{aligned} dZ^{[L]} &= A^{[L]}-Y \\ dW^{[L]} &= \frac 1m dZ^{[L]}A^{[L-1]T} \\ db^{[L]} &= \frac 1m \,sum(dZ^{[L]}) \end{aligned} dZ[L]dW[L]db[L]=A[L]−Y=m1dZ[L]A[L−1]T=m1sum(dZ[L]) -
隐含层
d A [ l ] = W [ l + 1 ] T d Z [ l + 1 ] d Z [ l ] = d A [ l ] g ′ [ l ] ( Z [ l ] ) d W [ l ] = 1 m d Z [ l ] A [ l − 1 ] T d b [ l ] = 1 m s u m ( d Z [ l ] ) \begin{aligned} dA^{[l]} &= W^{[l+1]T}dZ^{[l+1]} \\ dZ^{[l]} &= dA^{[l]}g^{'[l]}(Z^{[l]}) \\ dW^{[l]} &= \frac 1m dZ^{[l]}A^{[l-1]T} \\ db^{[l]} &= \frac 1m \,sum(dZ^{[l]}) \end{aligned} dA[l]dZ[l]dW[l]db[l]=W[l+1]TdZ[l+1]=dA[l]g′[l](Z[l])=m1dZ[l]A[l−1]T=m1sum(dZ[l])
。。。
d A [ 1 ] = W [ 2 ] T d Z [ 2 ] d Z [ 1 ] = d A [ 1 ] g ′ [ 1 ] ( Z [ 1 ] ) d W [ 1 ] = 1 m d Z [ 1 ] X T d b [ 1 ] = 1 m s u m ( d Z [ 1 ] ) \begin{aligned} dA^{[1]} &= W^{[2]T}dZ^{[2]} \\ dZ^{[1]} &= dA^{[1]}g^{'[1]}(Z^{[1]}) \\ dW^{[1]} &= \frac 1m dZ^{[1]}X^T \\ db^{[1]} &= \frac 1m \,sum(dZ^{[1]}) \end{aligned} dA[1]dZ[1]dW[1]db[1]=W[2]TdZ[2]=dA[1]g′[1](Z[1])=m1dZ[1]XT=m1sum(dZ[1])
g ′ [ l ] g^{'[l]} g′[l] 表示第 l 层激活函数的导数,通常隐含层采用relu,输出层采用sigmoid(二分类)或者softmax(多分类)。
在 dW 和 db 中都有一个 1 m \frac 1m m1, 这是因为正向计算时有 m 个样本,所以这里需要除以 m
3.3 更新参数
W [ 1 ] : = W [ 1 ] − α d W [ 1 ] b [ 1 ] : = b [ 1 ] − α d b [ 1 ] \begin{aligned} W^{[1]}:&=W^{[1]} - \alpha\,dW^{[1]} \\ b^{[1]}:&=b^{[1]} - \alpha\,db^{[1]} \\ \end{aligned} W[1]:b[1]:=W[1]−αdW[1]=b[1]−αdb[1]
。。。
W [ l ] : = W [ l ] − α d W [ l ] b [ l ] : = b [ l ] − α d b [ l ] \begin{aligned} W^{[l]}:&=W^{[l]} - \alpha\,dW^{[l]} \\ b^{[l]}:&=b^{[l]} - \alpha\,db^{[l]} \\ \end{aligned} W[l]:b[l]:=W[l]−αdW[l]=b[l]−αdb[l]
。。。
W [ L ] : = W [ L ] − α d W [ L ] b [ L ] : = b [ L ] − α d b [ L ] \begin{aligned} W^{[L]}:&=W^{[L]} - \alpha\,dW^{[L]} \\ b^{[L]}:&=b^{[L]} - \alpha\,db^{[L]} \\ \end{aligned} W[L]:b[L]:=W[L]−αdW[L]=b[L]−αdb[L]
其中 α \alpha α 为学习率
经过多轮迭代即可得到最优的(W,b)。
四、输出层 dZ 探究
大家是否注意到,反向传播中
d Z [ L ] = A [ L ] − Y dZ^{[L]} = A^{[L]}-Y dZ[L]=A[L]−Y
理论上来说输出层的dZ
d Z = ∂ L o s s ∂ A ∂ A ∂ Z = ∂ L o s s ∂ A g ′ ( Z ) dZ = \frac{\partial Loss}{\partial A}\frac{\partial A}{\partial Z} = \frac{\partial Loss}{\partial A} \,g'(Z) dZ=∂A∂Loss∂Z∂A=∂A∂Lossg′(Z)
也就是当 Loss 或激活函数不同时,dZ 应该不同,这里为啥都是 dZ = A - Y 呢?
下面我们推导一下。
4.1 回归问题: 没有激活函数
回归问题:没有激活函数,即 A = Z。
损失函数 Loss 为样本误差的平方和
L o s s = 1 2 ∑ i = 1 m ( y ^ i − y i ) 2 = 1 2 ( A − Y ) 2 \begin{aligned} Loss &= \frac12\sum_{i=1}^m (\hat y_i - y_i)^2 \\ &= \frac12(A - Y)^2 \end{aligned} Loss=21i=1∑m(y^i−yi)2=21(A−Y)2
A 的偏导数为
∂ L o s s ∂ A = A − Y \frac{\partial Loss}{\partial A} = A - Y ∂A∂Loss=A−Y
因为 A = Z A = Z A=Z,所以 d Z = A − Y dZ = A - Y dZ=A−Y
4.2 二分类问题:激活函数为 sigmoid
二分类问题激活函数为 sigmoid,损失函数Loss为交叉熵
L o s s = − ( Y ln A + ( 1 − Y ) ln ( 1 − A ) ) Loss = -(Y\,\ln A + (1-Y)\,\ln (1-A)) Loss=−(YlnA+(1−Y)ln(1−A))
A 的偏导数为
∂ L ∂ A = − Y A + 1 − Y 1 − A \frac{\partial L}{\partial A} = -\frac{Y}{A} + \frac{1-Y}{1-A} ∂A∂L=−AY+1−A1−Y
Z 的偏导数为
d Z = ∂ L ∂ A ∂ A ∂ Z = ( − Y A + 1 − Y 1 − A ) ⋅ A ( 1 − A ) = A − Y \begin{aligned} dZ &= \frac{\partial L}{\partial A}\; \frac{\partial A}{\partial Z} \\ &= (-\frac{Y}{A} + \frac{1-Y}{1-A})\cdot A(1-A) \\ &= A-Y \end{aligned} dZ=∂A∂L∂Z∂A=(−AY+1−A1−Y)⋅A(1−A)=A−Y
sigmoid 导数 A’(Z) = A(1-A)
4.3 多分类问题:激活函数为 softmax
4.3.1 多分类与 One Hot
在多分类任务中, 比如手势识别中,真实的手势可能是 (0, 1,2,3,4,5), 在输入计算机的时候,Y 需要进行 one hot 编码,比如手势有 6 个类别,需要把 y 编码成长度为6的向量,向量的每个值代表这个类别是否命中,命中为 1,不命中为 0。因为手势只能属于一个类别,所以每个向量中仅有一个 1,其他都为 0,1 的位置好像一个热点,所以称为 “One Hot”。
4.3.2 关于 softmax
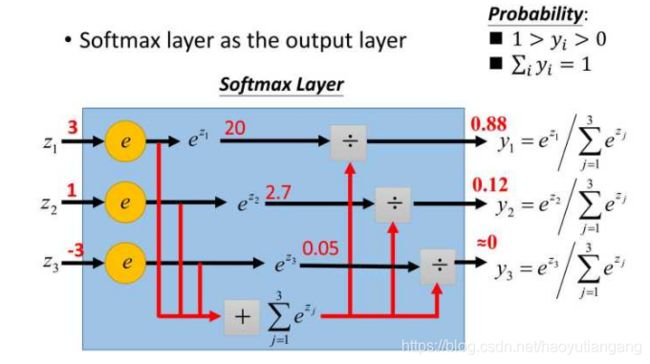
s o f t m a x ( Z ) = A = e Z j ∑ k e Z k softmax(Z) = A = \frac{e^{Z_j}}{\sum_{k} e^{Z_k}} softmax(Z)=A=∑keZkeZj
在多分类任务中,输出层 Z 的节点(维度)数等于分类个数,图中三分类的任务Z = {z1, z2, z3}。而 softmax 的任务是放大各项的比例关系,使最大的占比尽量接近 1,其他的占比尽量接近 0,这样才方便和经过“One Hot” 编码的真实的 Y 去比较。
softmax 分母是为了保证向量各项的和为 1。
4.3.3 多分类 softmax 中 dZ 的求解
多分类任务中使用 softmax 作为激活函数,损失函数Loss为交叉熵。
L o s s = − Y ln A = − ∑ j Y j ln A j Loss = -Y\ln A = -\sum_j Y_j \ln A_j Loss=−YlnA=−j∑YjlnAj
因为 d Z = ∂ L ∂ A ∂ A ∂ Z dZ = \frac{\partial L}{\partial A}\; \frac{\partial A}{\partial Z} dZ=∂A∂L∂Z∂A, 下面我们分布来求解:
- 求解 ∂ L ∂ A \frac{\partial L}{\partial A} ∂A∂L
∂ L ∂ A = − ∑ j Y j A j \frac{\partial L}{\partial A} =-\sum_j \frac{Y_j}{A_j} ∂A∂L=−j∑AjYj
- 求解 ∂ A ∂ Z \frac{\partial A}{\partial Z} ∂Z∂A
∂ A ∂ Z = ∂ e Z j ∑ k e Z k ∂ Z i \begin{aligned} \frac{\partial A}{\partial Z} = \frac{\partial \frac{e^{Z_j}}{\sum_{k} e^{Z_k}}}{\partial Z_i} \end{aligned} ∂Z∂A=∂Zi∂∑keZkeZj
下面分别讨论 i = j i=j i=j 和 i ≠ j i \ne j i=j 的情况:
切记 s o f t m a x ( Z ) = A = e Z j ∑ k e Z k softmax(Z) = A = \frac{e^{Z_j}}{\sum_{k} e^{Z_k}} softmax(Z)=A=∑keZkeZj
当 i = j i = j i=j 时:
∂ e Z i ∑ k e Z k ∂ Z i = ∑ k e Z k e Z i − ( e Z i ) 2 ( ∑ k e Z k ) 2 = ( e Z i ∑ k e Z k ) ( 1 − e Z i ∑ k e Z k ) = A i ( 1 − A i ) \begin{aligned} &\frac{\partial \frac{e^{Z_i}}{\sum_{k} e^{Z_k}}}{\partial Z_i} \\ &= \frac{\sum_{k} e^{Z_k}e^{Z_i} - (e^{Z_i})^2}{(\sum_{k} e^{Z_k})^2} \\ &= (\frac{e^{Z_i}}{\sum_{k} e^{Z_k}})(1-\frac{e^{Z_i}}{\sum_{k} e^{Z_k}}) \\ &= A_i(1-A_i) \end{aligned} ∂Zi∂∑keZkeZi=(∑keZk)2∑keZkeZi−(eZi)2=(∑keZkeZi)(1−∑keZkeZi)=Ai(1−Ai)
当 i ≠ j i \ne j i=j 时:
∂ e Z j ∑ k e Z k ∂ Z i = − e Z j ( 1 ∑ k e Z k ) 2 e Z i = − ( e Z i ∑ k e Z k ) ( e Z j ∑ k e Z k ) = − A i A j \begin{aligned} &\frac{\partial \frac{e^{Z_j}}{\sum_{k} e^{Z_k}}}{\partial Z_i} \\ &= - e^{Z_j} (\frac 1 {\sum_{k} e^{Z_k}})^2e^{Z_i} \\ &= -(\frac{e^{Z_i}}{\sum_{k} e^{Z_k}})(\frac{e^{Z_j}}{\sum_{k} e^{Z_k}}) \\ &= -A_iA_j \end{aligned} ∂Zi∂∑keZkeZj=−eZj(∑keZk1)2eZi=−(∑keZkeZi)(∑keZkeZj)=−AiAj
- 求解 d Z = ∂ L ∂ A ∂ A ∂ Z dZ = \frac{\partial L}{\partial A}\; \frac{\partial A}{\partial Z} dZ=∂A∂L∂Z∂A
d Z = ∂ L ∂ A ∂ A ∂ Z = ∑ j ∂ L j ∂ A j ∂ A j ∂ Z i = ∑ i = j ∂ L i ∂ A i ∂ A i ∂ Z i + ∑ i ≠ j ∂ L j ∂ A j ∂ A j ∂ Z i = ( − Y i A i ) ( A i ( 1 − A i ) ) + ∑ i ≠ j ( − Y j A j ) ( − A i A j ) = − Y i + Y i A i + ∑ i ≠ j Y j A i = A i ∑ i ≠ j Y j − Y i \begin{aligned} dZ &= \frac{\partial L}{\partial A}\; \frac{\partial A}{\partial Z} \\ &= \sum_j \frac{\partial L_j}{\partial A_j}\; \frac{\partial A_j}{\partial Z_i} \\ &= \sum_{i=j} \frac{\partial L_i}{\partial A_i}\; \frac{\partial A_i}{\partial Z_i} + \sum_{i \ne j} \frac{\partial L_j}{\partial A_j}\; \frac{\partial A_j}{\partial Z_i} \\ &= (-\frac{Y_i}{A_i})(A_i(1-A_i)) + \sum_{i \ne j}(-\frac{Y_j}{A_j})(-A_iA_j) \\ &= -Y_i+Y_iA_i + \sum_{i \ne j}Y_jA_i \\ &= A_i\sum_{i \ne j}Y_j - Y_i \end{aligned} dZ=∂A∂L∂Z∂A=j∑∂Aj∂Lj∂Zi∂Aj=i=j∑∂Ai∂Li∂Zi∂Ai+i=j∑∂Aj∂Lj∂Zi∂Aj=(−AiYi)(Ai(1−Ai))+i=j∑(−AjYj)(−AiAj)=−Yi+YiAi+i=j∑YjAi=Aii=j∑Yj−Yi
而多分类问题中 Y 向量中只有一个是 1,其他都为0 。
- 当 Y i = 1 Y_i = 1 Yi=1 时, ∑ i ≠ j Y j = 0 \sum_{i \ne j}Y_j = 0 ∑i=jYj=0 所以 d Z = A i − 1 dZ = A_i - 1 dZ=Ai−1
- 当 Y i = 0 Y_i = 0 Yi=0 时, ∑ i ≠ j Y j = 1 \sum_{i \ne j}Y_j = 1 ∑i=jYj=1 所以 d Z = A i − 0 dZ = A_i - 0 dZ=Ai−0
以上两种情况统一为:
d Z i = A i − Y i dZ_i = Ai - Y_i dZi=Ai−Yi
所以
d Z = A − Y dZ = A - Y dZ=A−Y
4.4 总结
从推导过程可以看出,无论输出层是无激活函数的回归问题,还是 sigmoid 的二分类问题,又或者是 softmax 的多分类问题,dZ 推导出来的形式都一样。
d Z = A − Y dZ = A - Y dZ=A−Y
世界就是这么奇妙。
后记
深度神经网络先聊到这里,下次我们聊聊图片识别领域的神器–卷积神经网络(CNN)。
欢迎关注本人公众号《大数据茶馆》,用大白话畅聊大数据。
来的都是客,欢迎您常来坐坐~
![]()