OpenGL - 光照模型以及OpenGL中的设置
文章目录
- 1.1 Phong 光照明模型
- 1. 光照模型拆分
- 1. Ambient light
- 2. Diffuse reflection
- 3. Specular reflection
- 1.2 完整Phong模型
- 1.2 Blinn光照明模型
- 1.3 光亮度表达
- 1. 三色学说
- 2. 多分量计算
- 3. 多光源计算
- 1.4 简单模型的局限性
- 全局光照
- 1.5 OpenGL中光照设置
- 1. 设置好物体的法向
- 2. 打开光照开关
- 3. 设置光照参数
- 4. 设置材质参数
- 5. 设置聚光灯
- 6. 光照的衰减
- 7. 光照下物体的颜色
- 8. 光照明设置
- 1.6 几种光照模式
- 1. 方向性光源
- 2. 位置性光源
- 3. OpenGL中的设置
- 4. 本地和无限远视点
- 5. 光照模式设置
- 1.7 让光源运动
- 1.8 常数和Gouraud明暗处理
- 1. 常数明暗处理
- 2. Gouraud明暗处理
- 1.9 Phong 明暗处理
景物表面任一点被光照射后投向观察者眼中的光亮度的大小,实际上计算光照就是计算投向观察者眼中的光亮度以及颜色,将计算过程表达成一个数学公式就是所谓的光照明模型,这种模型不容易直接构建,因此把光分钟三种成分再去分别计算每种成分所独有的特性
- Ambient light(环境光)
- Diffuse reflection(漫反射)
- Specular reflection(镜面反射)
环境光是光源发出的光在场景中经过多次反射、折射后还会对物体产生的影响,环境光就是反映周围环境对物体的光照影响,因此环境光是最难模拟的
1.1 Phong 光照明模型
1. 光照模型拆分
1. Ambient light
环境光非常复杂,在Phong模型中只是采用了一个常数来表示 I e = K a I a I_e = K_aI_a Ie=KaIa
I a I_a Ia:环境光的亮度,因为很难计算,所以就用一个常数来表示
k a k_a ka:物体表面的环境光反射系数( K a ∈ [ 0 , 1 ] Ka \in [0, 1] Ka∈[0,1])
2. Diffuse reflection
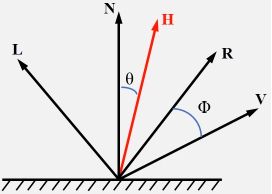
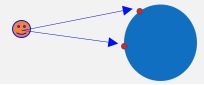
漫射光,(粗糙)凹凸不平的表面的光会向四周均匀反射,这种光与视点的位置是无关的
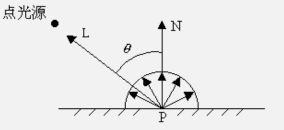
漫射光与入射光的角度的关系:入射光相对于物体表面越斜,反射光越弱,也即是入射光与法向夹角越大,反射越弱
Lamert 漫射光简单计算公式: I = K d I l cos θ I = K_dI_l\cos\theta I=KdIlcosθ,其中$\cos\theta = \vec{N}\cdot\vec{L} ( ( (\vec{N} 和 和 和\vec{L}$是单位向量)
-
I l I_l Il:表示 light 光
-
K d K_d Kd:表示 diffuse光的反射率或反射系数( K d ∈ [ 0 , 1 ] K_d\in[0,1] Kd∈[0,1])
使用 cos θ \cos\theta cosθ函数,是因为当入射光与法线的夹角 θ \theta θ是 0 时值最大,当角度是 π 2 \frac{\pi}{2} 2π的时候值最小,正好是一个曲线递减
3. Specular reflection
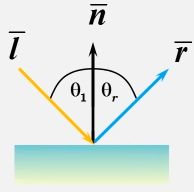
镜面反射入射角和反射角是一样的
其中入射光是 L ⃗ \vec{L} L反射光是 R ⃗ \vec{R} R, θ l = θ r \theta_l = \theta_r θl=θr,但是现实生活中并不存在绝对的镜面
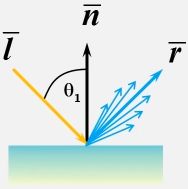
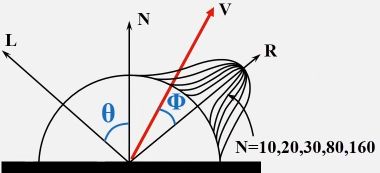
1973年,Phong BuiTuong 提出了计算高光的经验公式: I = K s I l cos n ϕ I = K_sI_l\cos^n\phi I=KsIlcosnϕ
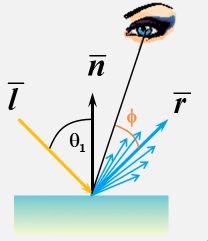
- K s K_s Ks:高光的反射系数( K s ∈ [ 0 , 1 ] K_s\in[0,1] Ks∈[0,1])
- I l I_l Il:光亮度
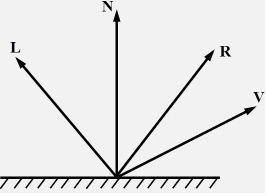
- cos ϕ \cos\phi cosϕ = R ⃗ ⋅ V ⃗ \vec{R} \cdot\vec{V} R⋅V( V ⃗ \vec{V} V是视线方向)
- n n n:高光指数,用来控制物体表面的光滑程度
其中 n n n越大,表明反射光反射区域越集中因此越光滑,越小表示反射区域比较大不是很光滑
1.2 完整Phong模型
将上面三者加起来之后就是完整的Phong Illumination Model(Phong光照明模型)
- A m b i e n t = K a I a Ambient = K_aI_a Ambient=KaIa
- D i f f u s e = K d I l cos θ Diffuse = K_dI_l\cos\theta Diffuse=KdIlcosθ
- S p e c u l a r = K s I l cos n ϕ Specular = K_sI_l\cos^n\phi Specular=KsIlcosnϕ
最后公式:
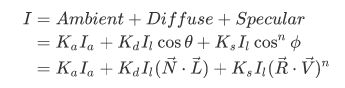
这种光照明模型是第一个得到广泛使用的照明模型,因为计算效率非常高并且效果还可以
1.2 Blinn光照明模型
从Phong模型中可以看到与视点位置无关的参数以及有关的参数
-
与 视 点 位 置 无 关 { K a I a K d I l ( N ⃗ ⋅ L ⃗ ) 与视点位置无关\begin{cases} K_aI_a\\ K_dI_l(\vec{N}\cdot\vec{L}) \end{cases} 与视点位置无关{KaIaKdIl(N⋅L)
-
与 视 点 位 置 有 关 { K s I l ( R ⃗ ⋅ V ⃗ ) n 与视点位置有关\begin{cases} K_sI_l(\vec{R}\cdot\vec{V})^n \end{cases} 与视点位置有关{KsIl(R⋅V)n
与视点的无关的参数比较好计算,因为不需要考虑视点的位置就能计算光亮度,与视点相关的参数就要在视点变化的时候重新计算
- 与光照有关的参数: I a , I l , L ⃗ I_a,I_l,\vec{L} Ia,Il,L( I a I_a Ia环境光, I l I_l Il光亮度, L ⃗ \vec{L} L光照方向)
- 与材质有关的参数: K a , K d , K s , n , N ⃗ K_a,K_d,K_s,n,\vec{N} Ka,Kd,Ks,n,N(反射系数,高光指数和法向量)
Phong模型中比较难计算的是 R ⃗ = 2 N ⃗ ( N ⃗ ⋅ L ⃗ ) − L ⃗ \vec{R} = 2\vec{N}(\vec{N}\cdot\vec{L})-\vec{L} R=2N(N⋅L)−L它是反射光方向
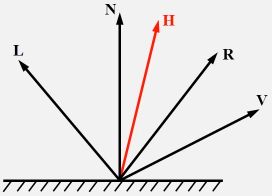
这个参数计算比较繁琐,会影响计算的效率,因此在实际应用中,常常使用 ( N ⃗ ⋅ H ⃗ ) (\vec{N}\cdot\vec{H}) (N⋅H)来代替 ( R ⃗ ⋅ V ⃗ ) (\vec{R}\cdot\vec{V}) (R⋅V)
H ⃗ \vec{H} H是沿 L ⃗ \vec{L} L和 V ⃗ \vec{V} V的角平分线的单位向量,即: H ⃗ = n o r m a l i z e ( L ⃗ + V ⃗ ) \vec{H} = normalize(\vec{L} + \vec{V}) H=normalize(L+V), H ⃗ \vec{H} H的计算就是简单的加分和单位化
- R ⃗ ⋅ V ⃗ = cos ϕ \vec{R}\cdot\vec{V} = \cos\phi R⋅V=cosϕ
- N ⃗ ⋅ H ⃗ = cos θ \vec{N}\cdot\vec{H} = \cos\theta N⋅H=cosθ
θ \theta θ是 ϕ \phi ϕ的一半,并且 θ \theta θ会随着 ϕ \phi ϕ的变化而变化,两者的变化趋势是一致的,因为本身Phong的 cos ϕ \cos\phi cosϕ就是纯经验式的计算,因此可以用 cos θ \cos\theta cosθ来代替 cos ϕ \cos\phi cosϕ;
Blinn 在1977年对Phong模型进行了改进,以 ( N ⃗ ⋅ H ⃗ ) (\vec{N}\cdot\vec{H}) (N⋅H)代替了 ( R ⃗ ⋅ V ⃗ ) (\vec{R}\cdot\vec{V}) (R⋅V)
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( N ⃗ ⋅ H ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{N}\cdot\vec{H})^n I=KaIa+KdIl(N⋅L)+KsIl(N⋅H)n
此模型即称为Phong-Blinn Model,这个因为计算效率较高,所以得到广泛的应用
1.3 光亮度表达
1. 三色学说
十九世纪初,Yaung提出某种波长的光可以通过三种不同波长的光混合而复现出来的假说,即红®、绿(G)和蓝(B)三原色,把三种原色按照不同的比例混合就能复现其他任何波长的光
通过Phong-Blinn Model得出一个值 I I I,这个值是物理上光亮度值,在计算机中采用 R , G , B R,G,B R,G,B三种颜色来表示,因此计算 I I I的时候,需要对 r g b rgb rgb三个分量分别进行计算,得出这个三个分量的值
2. 多分量计算

而且也可以分别对每一个反射系数的每一个分量设置不同的值,来表示更加丰富的材质效果
3. 多光源计算
但是上面的公式计算的单光源效果,那么如果有多盏灯的话应该如何计算光亮度,其实只要把每盏灯的计算结果加起来就可以了,假设有 M M M盏灯,那么计算公式如下,环境光 K a I a K_aI_a KaIa是唯一的
I = K a I a + ∑ i = 1 M [ K d I l i ( N ⃗ ⋅ L i ⃗ ) + K s I l i ( R ⃗ ⋅ V ⃗ ) n ] I = K_aI_a + \sum_{i = 1}^M [K_dI_{li}(\vec{N}\cdot\vec{L_i}) + K_sI_{li}(\vec{R}\cdot\vec{V})^n] I=KaIa+∑i=1M[KdIli(N⋅Li)+KsIli(R⋅V)n]
1.4 简单模型的局限性
- 仅考虑光源直接照射的效果 – (Direct Illumination)直接光照
- 并没有考虑非光源直接照射的效果 – (Interreflections Illumination)间接光照
全局光照
Global Illumination(全局光照模拟) = 直接光照 + 间接光照
- Ray tracing (光线跟踪,1980),考虑了光滑表面对环境光的反射和折射
- Radiosity (辐射度,1984),能够模拟漫射表面的颜色辉映的效果
- Photon Mapping(光子映射,1994),可以更有效的模拟镜面反射以及漫反射效果
1.5 OpenGL中光照设置
步骤如下:
1. 设置好物体的法向
glNormal3f(Nx,Ny,Nz);//计算法向量
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( N ⃗ ⋅ H ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{N}\cdot\vec{H})^n I=KaIa+KdIl(N⋅L)+KsIl(N⋅H)n
2. 打开光照开关
glEnable(GL_LIGHTING);//打开光照
glEnable(GL_LIGHT0);//打开第一盏灯
具体如何计算物体的法向,法向就是和物体表面垂直的方向
物体是由多边形面片组成,那么可以计算面片的法向
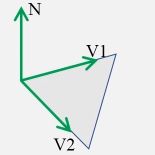
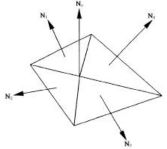
例如: v 1 ⃗ \vec{v_1} v1和 v 2 ⃗ \vec{v_2} v2的法向就是 N ⃗ \vec{N} N,也即是 N ⃗ = v 1 ⃗ v 2 ⃗ \vec{N} = \vec{v_1}\vec{v_2} N=v1v2,但是物体表面不只有平面,因此常计算的是点的法向
把点周围的三角面的法向都计算出来,然后求一个平均值既可
3. 设置光照参数
通过函数glLightfv()来设置光照参数
glLightfv(GL_LIGHT0, GL_AMBIENT, vLitAmbient); // Ia
glLightfv(GL_LIGHT0, GL_DIFFUSE, vLitDiffuse); // Il
glLightfv(GL_LIGHT0, GL_SPECULAR, vLitSpecular);// Il
还需要设置光源的位置
glLightfv(GL_LIGHT0, GL_POSITION, vLitPosition)
4. 设置材质参数
通过函数glMaterialfv()来设置材质参数
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( N ⃗ ⋅ H ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{N}\cdot\vec{H})^n I=KaIa+KdIl(N⋅L)+KsIl(N⋅H)n
glMaterialfv(GL_FRONT, GL_AMBIENT, vMatAmb); // vMatAmb对应光照方程中 ka 反射系数
glMaterialfv(GL_FRONT, GL_DIFFUSE, vMatDif); // vMatDif对应光照方程中 kd 反射系数
glMaterialfv(GL_FRONT, GL_SPECULAR, vMatSpe);// vMatSpe对应光照方程中 ks 反射系数
glMaterialfv(GL_FRONT, GL_SHININESS, vShininess);// 对应光照方程中 n 高光指数
glMaterialfv(GL_FRONT, GL_EMISSION, vEmission);// vEmission 自发光
GL_FRONT/GL_BACK/GL_FRONT_AND_BACK
分别是物体的前向面、后向面和前后相面,对应于法向的朝向是前向面
5. 设置聚光灯
glLightfv(GL_LIGHT0, GL_SPOT_DIRECTION, vSpotDir);// 聚光灯的方向
glLightfv(GL_LIGHT0, GL_SPOT_CUTOFF, vLitCutoff); // 聚光灯的角度
glLightfv(GL_LIGHT0, GL_SPOT_EXPONENT, vSpotExp); // 聚光灯的衰减
6. 光照的衰减
在OpenGL中可以设置光随着距离衰减的相关参数
glLightfv(GL_LIGHT0, GL_CONSTANT_ATTENUATION, kc);// kc 常数衰减
glLightfv(GL_LIGHT0, GL_LINEAR_ATTENUATION, kl);// kl 线性衰减
glLightfv(GL_LIGHT0, GL_QUADRATIC_ATTENUATION , kq); // kq 指数衰减
衰减因子: 1 k c + k l d + k q d 2 \frac{1}{k_c + k_ld + k_qd^2} kc+kld+kqd21
- d d d:光源到顶点的间的距离,d越大光线越暗,衰减因子越小
k c k_c kc的默认值是 1 1 1, k l k_l kl和 k 1 k_1 k1的默认值是 0 0 0,默认情况下无衰减,所有OpenGL的状态参数都有一个默认值
7. 光照下物体的颜色
光照下物体的颜色由谁来决定的,可以通过下面两个函数来设置
- 光的颜色:
glLightfv()函数 - 物体的材质:
glMaterialfv()
那么 glColor*()是否还起到设置颜色的作用,实际上一旦设置了光照,那么glColor*()设置的颜色就会自动失效,因为在计算物体的颜色的时候不再考虑glColor*()中设置的颜色,但是也可以通过设置来让glColor*()中的颜色作为材质与灯光产生计算
glEnable(GL_COLOR_MATERIAL);// 作为颜色材质
glColorMaterial(GL_FRONT_AND_BACK, GL_AMBIENT);// 赋值为环境光,此时不再需要赋值环境光
8. 光照明设置
- OpenGL中的光照明模型
- 设置物体的法向
- 设置光照参数的语句
- 设置材质参数的语句
- 聚光灯参数
- 光照衰减参数
- 方向光源与位置光源
- 本地视点、无限远视点
- 双面光照
1.6 几种光照模式
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( N ⃗ ⋅ H ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{N}\cdot\vec{H})^n I=KaIa+KdIl(N⋅L)+KsIl(N⋅H)n
在计算光照的时候,光照的位置比较中,在方程中是向量 L ⃗ \vec{L} L,点到光源连成的向量就是 L ⃗ \vec{L} L,但实际上又分为两种,方向性光源和位置性光源
1. 方向性光源
所谓方向性光源就是模拟太阳和月亮光的效果,从太阳发出的光线,到物体的表面与所有点连成的向量 L ⃗ \vec{L} L方向都是一样也就是平行光
2. 位置性光源
当模拟的是室内的灯,此时光源与物体表面的点组成的向量就不是平行的了,对每一个点都要计算不同的光照方向
3. OpenGL中的设置
Glfloat vLitPosition[] = {1.0, 1.0, 1.0, 0.0};
glLightfv(GL_LIGHT0, GL_POSITION, vLitPosition);
若vLitPosition的第四个分量w为0.0,则为方向性光源,否则是位置性光源
4. 本地和无限远视点
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( R ⃗ ⋅ V ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{R}\cdot\vec{V})^n I=KaIa+KdIl(N⋅L)+KsIl(R⋅V)n
视点在光照明方程中的决定值是 V ⃗ \vec{V} V或者是 H ⃗ \vec{H} H
如果视点距离物体比较近的话,需要依次计算视点到物体顶点的方向,这就是本地视点
如果视点距离物体很远的话,可以采用一种简化策略,大概视线方向是平行的,这个就是无限远视点
OpenGL中通过函数glLightModelf()来设置
glLightModelf(GL_LIGHT_MODEL_LOCAL_VIEWER, GL_TRUE);//最后一个参数为 true时是本地视点,否则是无限远视点
5. 光照模式设置
双面光照就是,物体的正向面面和被向面都进行光照计算,如果把双面光照关闭的话,物体内表面的光照就是常数计算,如果是一个封闭的物体,可以采用非双面光照计算,可以节省计算量
I = K a I a + K d I l ( N ⃗ ⋅ L ⃗ ) + K s I l ( R ⃗ ⋅ V ⃗ ) n I = K_aI_a + K_dI_l(\vec{N}\cdot\vec{L}) + K_sI_l(\vec{R}\cdot\vec{V})^n I=KaIa+KdIl(N⋅L)+KsIl(R⋅V)n
依据光照明方程,正向面用参数 N ⃗ \vec{N} N,背向面就需要用 − N ⃗ - \vec{N} −N来计算光照
1.7 让光源运动
在OpenGL中设置光源的函数是glLightfv()
glLightfv(GL_LIGHT0, GL_POSITION, vLitPosition);// 可以直接变化 vLitPosition,来使光源运动
更常用的方法是,把光源看成一个几何物体,可以通过几何的矩阵变换的方法来影响光源的位置,例如下面的代码
GLfloat pos[4] = {1.50, 1.00, 1.00, 0.00}; //光源位置
glLightfv(GL_LIGHT0, GL_POSITION, pos);// 设置光源
gluLookAt(0.00, 0.00, 2.00, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00);//可以通过修改视点的参数,来影响光源位置的变换
1.8 常数和Gouraud明暗处理
在顶点处理阶段,计算出了三角形每个顶点的光照,三角形所覆盖的每个像素的光照值在光栅化阶段可以得到,所谓明暗处理就是着色,也就是计算三角形内每个像素颜色的过程
1. 常数明暗处理
在默认的图形流水线中,由于效率的原因,光照计算是为每个顶点进行的,所谓常数明暗处理就是对每个多边形只计算一个光照强度值,然后用此值作为整个多边形平面的明暗强度值,然后用此值作为整个多边形平面的明暗值赋给多边形的每个像素,使多边形的每个点都具有相同的明暗度
上面就是常数明暗处理球体的效果,面片的颜色可能是来自于三角形的某一个顶点,显示的有棱角的效果
2. Gouraud明暗处理
Gouraud 采用双线性差值的方式计算面片内的像素的颜色,步骤大概如下
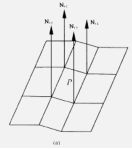
- 首先计算出多边形各定点的法向,方法是对周围面片的法向进行平均求得此定点的法向
- 计算出多边形各定点处的光亮度值
- 然后再对多边形定点的光亮度值进行“双线性差值”计算出多边形内任一片元的光亮度
首先,对求出顶点周围面片的法向(三角面片的法向就是两个边长向量的叉积的单位化),然后对这些法向进行平均之后就求得此定点的法向
双线性差值
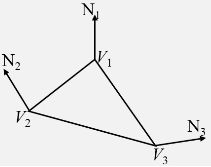
在光栅化过程中会对多边形进行扫描转换,所以沿当前三角面扫描线,先差值计算出a和b两点的光亮度

I a = u × I 1 + ( 1 − u ) × I 2 , u = a V 2 ÷ V 1 V 2 I_a = u \times I_1 + (1 - u) \times I_2,u = aV_2 \div V_1V_2 Ia=u×I1+(1−u)×I2,u=aV2÷V1V2
I b = v × I 1 + ( 1 − v ) × I 3 , v = b V 3 ÷ V 1 V 3 I_b = v \times I_1 + (1 - v) \times I_3,v = bV_3 \div V_1V_3 Ib=v×I1+(1−v)×I3,v=bV3÷V1V3
然后再由a,b两点的光亮度差值计算出P点的光亮度值
I p = t × I a + ( 1 − t ) × I b , t = P b ÷ a b I_p = t\times I_a + (1 - t)\times I_b,t = P_b \div ab Ip=t×Ia+(1−t)×Ib,t=Pb÷ab
I p = ( t u + v − t v ) × I 1 + ( t − t u ) × I 2 + ( 1 − t − v + t v ) × I 3 I_p = (tu + v - tv) \times I_1 + (t - tu) \times I_2 + (1 - t - v + tv) \times I_3 Ip=(tu+v−tv)×I1+(t−tu)×I2+(1−t−v+tv)×I3
光照计算三个步骤的发生阶段
- 计算多边形各定点的法向 – CPU
- 计算多边形各定点处的光亮度值 – vertex operation
- 对多边形定点的光亮度值进行双线性差值,计算出多边形内任一片元的光亮度 – rasterization
OpenGL中的 Flat Shading对应的就是常数明暗处理,Smooth Shading对应的是Gourand明暗处理
1.9 Phong 明暗处理
Grouraud 明暗处理的弊端
- 曲面分割过粗可能产生错误效果
- 高光的丢失
- 马赫带效应(即光亮程度变化率不连续的便捷呈现亮带或黑带)
平面不连续时产生的错误,可以提供过曲面细分来补救,但是效率会变慢
Phong 明暗处理思想
不是差值光亮度颜色,而是差值法向量,因此也称为 法向量差值明暗处理,就是对多边形定点处法向量做双线性差值,将插值计算得到的多边形内个片元的法向量带入光亮度计算公式,得到个片元的光亮度,主要步骤如下
- 计算出多边形各顶点的法向
- 对多边形中的某个片元,双线性插值计算其法向量,对法向量进行双线性插值
- 计算出多边形内该片元的光亮度
Gouraud 是计算出顶点光亮度,然后对光亮度进行插值,Phong 是先插值计算出法向量,Phong 模拟了光滑表面的法向的变化,因此效果更好,高光区域更加集中
三种明暗处理方法
- 三种方法效果越来越好,但是计算量也越来越大
- 常数和Gouraud明暗处理是顶点级别的光照计算,而Phong 是Shading 是像素级别的光照计算