CVPR2020-HRank：Filter Pruning using High-Rank Feature Map

1. 介绍

滤波器修剪的核心在于滤波器的选择，滤波器的选择应以最高的压缩比和最低的精度折衷。基于过滤器评价函数的设计，作者根据经验将过滤器剪枝分为两种大类。
属性的重要性(Property Importance)：基于CNNs的固有属性对滤波器进行修剪。这些修剪方法不会弥补网络训练损失。剪枝后，通过微调提高模型性能。在这些方法中:

1. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures利用大型网络中输出的稀疏性，去除零激活率较高的滤波器（APOZ方法）。
2. Pruning filters for efficient convnets.基于“1-范数”的剪枝，假设具有较小范数的参数或特征信息量较少，因此应首先剪枝。
3. Pruning convolutional neural networks for resource efficient inference提出考虑了一阶梯度来评价滤波器的重要性，去掉了最不重要的滤波器。
4. Nisp: Pruning networks using neuron importance score propagation 对最终响应的重要性评分被传播到网络中的每个过滤器，并通过删除重要性最低的一个来修剪CNNs。
5. Filter pruning via geometric median for deep convolutional neural networks acceleration.计算图层中的几何中值，并修剪最接近该中值的过滤器。

大多数滤波器评价函数的设计都是自设计的，这带来了时间复杂度低的优点，但也限制了加速比和压缩比。
适应性属性：方法将剪枝要求嵌入到网络训练损失中，通过联合再训练优化生成自适应剪枝决策。

• Learning efficient convolutional networks through network slimming.和Variational convolutional neural network pruning.对BN层的尺度因子施加了稀疏约束，使得具有较低尺度因子的通道被认为是不重要的。
• Data-driven sparse structure selection for deep neural networks.和Towards optimal structured cnn pruning via generative adversarial learning引入了新的比例因子参数(也称为掩码)来学习稀疏结构修剪，其中删除了与比例因子为零对应的过滤器。

与基于属性重要性的滤波剪枝方法相比，基于自适应重要性的方法由于其联合优化，通常可以获得更好的压缩和加速效果。然而，由于损失发生了变化，所需的再培训步骤在机器时间和人力上都很繁重，通常需要另一轮超参数调整。
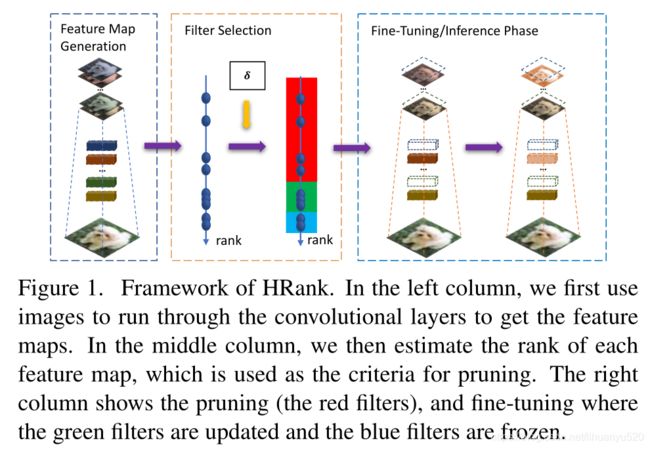
在这个论文中，提出了一种有效且高效的滤波器剪枝方法，该方法探索每一层特征图的高矩阵秩(HRank)。它是一种基于属性的修剪方法（不用重重新训练，简化了剪枝的复杂性）。作者通过观察发现，无论CNN看到多少数据，单个过滤器生成的feature map的平均秩总是相同的。这表明，只使用输入图像的一小部分就可以准确地估计深度cnn中特征图的秩，从而达到高效的目的。基于这一思想，用数学方法证明了秩越低的特征映射对精度的贡献越小。因此，可以首先删除生成这些特征映射的过滤器。

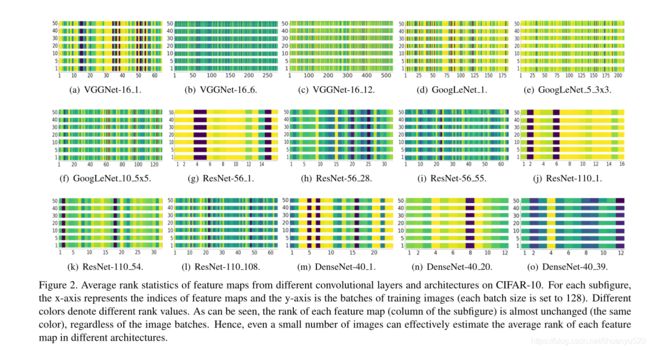
作者使用VGGNet、GoogLeNet、ResNet和DenseNet等许多具有代表性的大型CNN模型，在CIFAR-10和ImageNet这两个基准测试上进行了广泛的实验。结果表明HRank的性能优于现有的过滤剪枝方法，包括基于属性重要性的方法和最新的基于自适应重要性的模型。实验还表明，即使在剪枝后的微调过程中冻结了一部分高阶特征映射的滤波器，模型仍然保持了较高的精度，验证了我们的假设。
贡献有：

• 在大量统计验证的基础上，证明了单个滤波器生成的特征图的平均秩几乎没有变化。
• 从数学上证明，具有较低秩特征图的过滤器信息量较小，因此对保持准确性不太重要，可以首先删除这些准确性。
• 广泛的实验证明了HRank模型压缩和加速在各种最新技术状态下的效率和效果。

2. 方法

一个预先训练的模型有K层，$C^i$是第$i$个卷积层，滤波器可以用${\mathcal{W}}_{{\mathcal{C}}^i}=\left\{{\mathbf{w}}_1^i,{\mathbf{w}}_2^i,\dots ,{\mathbf{w}}_n^i\right\}\in {\mathbb{R}}^{n_i\times n_{i-1}\times k_i\times k_i}$表示，其中第$j$个滤波器为${\mathbf{w}}_j^i\in {\mathbb{R}}^{n_{i-1}\times k_i\times k_i}$。对于特征图我们定义为${\mathcal{O}}^i=\left\{{\mathbf{o}}_1^i,{\mathbf{o}}_2^i,\dots ,{\mathbf{o}}_{n_i}^i\right\}\in {\mathbb{R}}^{n_i\times g\times h_i\times w_i}$，其中第$j$个特征图${\mathbf{o}}_j^i\in {\mathbb{R}}^{g\times h_i\times w_i}$是由${\mathbf{w}}_j^i$生成。g是特征图的大小，$h_i$和$w_i$是特征图的高和宽。过滤器的剪枝可以将分为${\mathcal{W}}_{C^i}$分为两组，保留的子集${\mathcal{I}}_{{\mathcal{C}}^i}=\left\{{\mathbf{w}}_{{\mathcal{I}}_1^i}^i,{\mathbf{w}}_{{\mathcal{I}}_2^i}^i,\dots ,{\mathbf{w}}_{{\mathcal{I}}_{n_{i}1}^i}^i\right\}$和一个不重要将要被裁剪的子集${\mathcal{U}}_{{\mathcal{C}}^i}=\left\{{\mathbf{w}}_{{\mathcal{U}}_1^i}^i,{\mathbf{w}}_{{\mathcal{U}}_2^i}^i,\dots ,{\mathbf{w}}_{{\mathcal{U}}_{ni}^i}^i\right\}$，其中${\mathcal{I}}_j^i$ and ${\mathcal{U}}_j^i$分别是第$j$个重要的过滤器个不重要的过滤器。$n_{i1}$ and $n_{i2}$是重要和不重要滤波器的数量，于是有：${\mathcal{I}}_{{\mathcal{C}}^i}\cap {\mathcal{U}}_{{\mathcal{C}}^i}=\varnothing ,{\mathcal{I}}_{{\mathcal{C}}^i}\cup {\mathcal{U}}_{{\mathcal{C}}^i}={\mathcal{W}}_{{\mathcal{C}}^i}$ and $n_{i1}+n_{i2}=n_i$。
滤波器修剪的目的是找到不重要的滤波器并删除他们，这可以表示为一个优化问题。
$$\begin{array}{l}{\min }_{{\delta }_{ij}}{\sum }_{i=1}^K{\sum }_{j=1}^{n_i}{\delta }_{ij}\mathcal{L}\left({\mathbf{w}}_j^i\right)\\ \text{ s.t. }{\sum }_{j=1}^{n_i}{\delta }_{ij}=n_{i2}\end{array}$$
其中${\delta }_{ij}$，如果${\mathbf{w}}_j^i$被分组到${\mathcal{U}}_{C^i}$，则${\delta }_{ij}$是指示符1，或者如果${\mathbf{w}}_j^i$被分组到${\mathcal{I}}_{C^i}$，则为0。L(·)衡量过滤输入对CNN的重要性。因此，最小化上公式等于移除$C^i$中的$n_{i2}$个最不重要的滤波器。

作者认为，$L$在滤波器上的特别设计忽略了输入图像和输出标签的分布，这可能是基于属性重要性的方法表现出次优性能的原因。相反，在本文中，作者建议在特征映射上定义$L$。其基本原理在于，特征映射是既能反映滤波器属性又能反映输入图像的中间步骤,所以
$$\begin{array}{c}{\min }_{{\delta }_{ij}}{\sum }_{i=1}^K{\sum }_{j=1}^{n_i}{\delta }_{ij}{\mathbb{E}}_{I\sim P(I)}\left[\hat{\mathcal{L}}\left({\mathbf{o}}_j^i(I,:,:)\right)\right]\\ \text{ s.t. }{\sum }_{j=1}^{n_i}{\delta }_{ij}=n_{i2}\end{array}$$
其中$\hat{\mathcal{L}}(\cdot )$用于评估由${\mathbf{w}}_j^i$生成的特征图${\mathbf{o}}_j^i(I,:,:)$信息。特征图包含的信息越多，相应的滤波器就也越重要。作者利用了特征图的秩，它不仅被证明是一种有效的信息度量，而且在P(I)上也是一种稳定的表示。首先将我们的信息度量定义为：
$$\hat{L}\left({\mathbf{o}}_j^i(I,:,:)\right)=\mathbf{R}\mathrm{ank}\left({\mathbf{o}}_j^i(I,:,;)\right)$$
其中其中$Rank(\cdot )$是输入图像$I$的featre map的秩。我们对${\mathbf{o}}_j^i(I,:,:)$进行奇异值分解(SVD)：
$$\begin{array}{rl}{\mathbf{o}}_j^i(I,:,:)& =\sum _{i=1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T=\sum _{i=1}^{r^{\prime }}{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T+\sum _{i=r^{\prime }+1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T\end{array}$$
在其中$r=\mathrm{Rank}\left({\mathbf{o}}_j^i(I,:,;)\right)$，$r^{\prime }$<$r$，它可以看做将一个秩为$r$的feature map可以分解为一个低秩($r^{\prime }$)的特征图，即${\sum }_{i=1}^{r^{\prime }}{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T$；和一些额外的信息，即${\sum }_{i=r^{\prime }+1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T$，因此High-rank的特征图比Low-rank的特征图包含由更多的信息，因此rank可以作为信息丰富的度量。

使用小批量的输入图像来精确地估计特征图秩的期望
$${\mathbb{E}}_{I\sim P(I)}\left[\hat{\mathcal{L}}\left({\mathbf{o}}_j^i(I,:,:)\right)\right]\approx \sum _{t=1}^g\mathbf{R}\mathrm{ank}\left({\mathbf{o}}_j^i(t,:;;)\right)$$
最终：
$$\begin{array}{c}{\min }_{{\delta }_{ij}}{\sum }_{i=1}^K{\sum }_{j=1}^{n_i}{\delta }_{ij}\left({\mathbf{w}}_j^i\right){\sum }_{t=1}^g\mathbf{R}\mathrm{ank}\left({\mathbf{o}}_j^i(t,:,:)\right)\\ s.t.{\sum }_{j=1}^{n_i}{\delta }_{ij}=n_{i2}\end{array}$$

剪枝

举例说明输出的特征图为$32\ast 128\ast 128$，滤波器为$32\ast 16\ast 3\ast 3$

1. 我们计算16个通道对应特征图秩，并进行从大到小排序。
2. 我们决定要保存的滤波器个数$a$和不重要的的滤波器个数$b$,$a+b=32$
3. 然后我们通过索引值删除不重要的过滤器。
4. 最终我们在对网络进行微调。
   

实验

文章在小数据集和大数据集上进行了实验，即CIFAR-10和ImageNet。研究了不同算法在主流CNN模型上的性能，包括VGGNet、GoogLeNet、ResNet和DenseNet。对于所有基准和架构，随机抽样500张图像来估计每个特征图的平均秩。我们将以参数数量和所需浮点运算(表示为FLOP)，评估模型大小和计算要求。

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200622151607369.png?x-oss-process=image/w

• atermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2xpaHVhbnl1NTIw,size_16,color_FFFFFF,t_70)

Ablation study 消融实验

为了说明所提方案的合理性，作者又做了Ablation study。
**Variants of HRank.**为了证明high-rank特征图滤波器保存的适当性，提出了三种变体，包括：

• Edge：生成的high-rank和low-rank特征图的滤波器同时被修剪。
• Random：滤波器随意被修剪。
• Reverse：只修剪生成low-rank特征图的滤波器

：
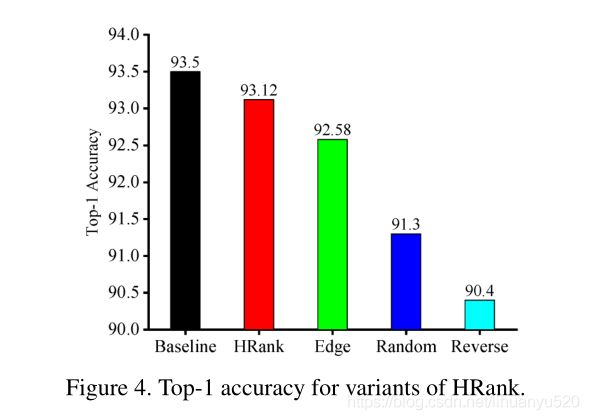
实验结果表明：low-rank特征映射包含的信息量较少，相应的滤波器可以安全地去除。
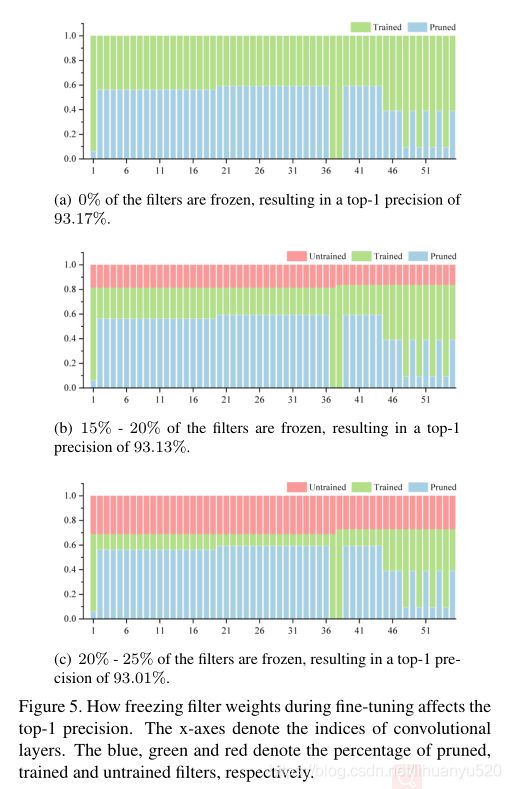
Freezing Filters during Fine-tuning 实验表明：不用High-rank特征映射更新滤波器对模型性能的影响不大。