求解最长公共子序列（Longest Common Subsequence,LCS）

    两个序列X和Y的公共子序列中，长度最长的那个，就是X和Y的最长公共子序列。最长公共子序列不要求连续，二最长公共子串要求连续。

思路：

  字符串X，长度为m；字符串Y，长度为n。Xi=即X序列的前i个字符，Yj=即Y序列的前j个字符，LCS（X,Y）为字符串X和Y的最长公共子序列，即Z=。

    假设xm，yn分别为X和Y的最后一个字符，而且xm=yn，那么Xm与Yn的最长公共子序列Zk的最后一个字符比定位xm(yn)。

即：

zk=xm=yn；LCS(Xm，Yn）=LCS(X(m-1)，Y(n-1)）+xm

如果xm!=yn，则：

要么：LCS(Xm,Yn)=LCS(X(m-1),Yn)

要么：LCS(Xm,Yn)=LCS(Xm,Y(n-1)) 

 即LCS(Xm,Yn)=max{LCS(X(m-1),Yn),LCS(Xm,Y(n-1))}

显然，这是动态规划问题

如何实现该算法：用到了长度数组，二维数组C[m,n],c[i,j]记录序列Xi和Yj的最长公共子序列的长度。

当i=0或j=0时，空序列是Xi和Yj 的最长公共子序列，所以c[i,j]=0。代码中该数组为ch

举例：X= Y=，LCS为BCBA

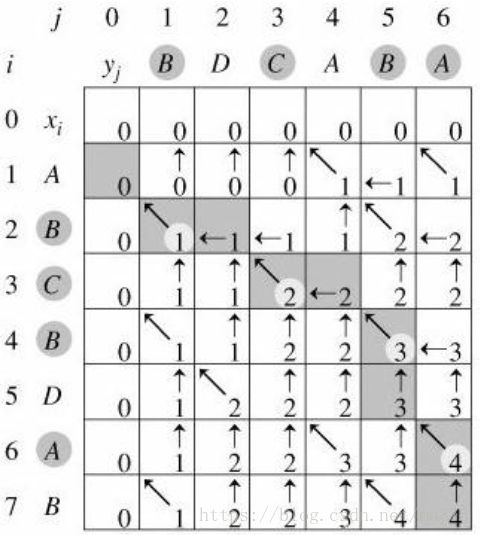
距离数组为：

注：箭头为求解LCS时回溯的方向，可以看出LCS的解并不唯一

import java.util.Scanner;
import java.util.Stack;

public class getLCS {
 
	public static void  main(String[] args)
	{
		@SuppressWarnings("resource")
		Scanner scan=new Scanner(System.in);
		System.out.println("请输入第一个字符串：");
		String str1=scan.nextLine();
		System.out.println("请输入第二个字符串：");
		String str2=scan.nextLine();
		int length=getLCSlength(str1, str2);
		System.out.println("最长公共子序列的长度为："+length);
		System.out.println("最长公共子序列为："+getLCS(str1, str2));
		
	}
	//构造cheese二维数组
	public static int[][] getCheese(String str1,String str2)
	{
		int size1=str1.length();
		int size2=str2.length();
		//int length1,length2=0;
		int[][] cheese=new int[size1+1][size2+1];
		for(int i=0;i str=new Stack();
		String result="";
		int size1=str1.length();
		int size2=str2.length();
		int[][] cheese=getCheese(str1, str2);
		int i=size1;
		int j=size2;
		while((i!=0)&&(j!=0))
		{
			if(str1.charAt(i-1)==str2.charAt(j-1))
				{
					str.push(str1.charAt(i-1));
					i--;
					j--;
				}
			else{
				if(cheese[i-1][j]>cheese[i][j-1])
					i--;
				else
					j--;
			}
		}
		while(!str.isEmpty())
		{
			result=result+str.pop();
		}
		return result;
	}