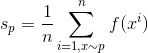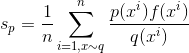随机采样知识点整理(Monte Carlo、接受-拒绝采样、重要性采样、MCMC)
蒙特卡洛法(Monte Carlo Method)
常用于计算一些非常复杂无法直接求解的函数期望。即按一定的概率分布中获取大量样本,用于计算函数在样本的概率分布上的期望。比如,抛硬币,做N次实验,统计正面朝上的次数,期望为正面朝上的次数/总次数。
其中最关键的步骤是:如何按照指定的概率分布![]() 进行样本采样
进行样本采样
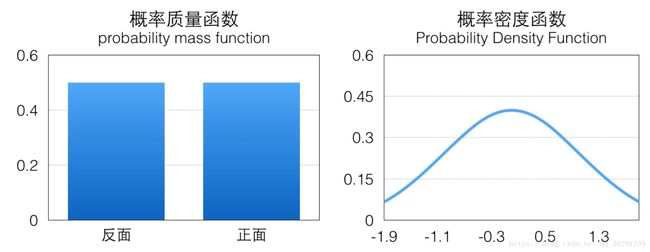
离散的概率分布用概率质量函数(pmf)表示
连续的概率分布用概率密度函数(pdf)表示
接受-拒绝采样(Acceptance-Rejection Sampling)
很多实际问题中,![]() 是很难直接采样的,因此,需要借助其他手段来采样。既然
是很难直接采样的,因此,需要借助其他手段来采样。既然![]() 太复杂在程序中没法直接采样,那么我设定一个程序可抽样的分布q(z)比如高斯分布,然后按照一定的方法拒绝某些样本,达到接近
太复杂在程序中没法直接采样,那么我设定一个程序可抽样的分布q(z)比如高斯分布,然后按照一定的方法拒绝某些样本,达到接近![]() 分布的目的,其中q(z)叫做建议分布(proposal distribution)。
分布的目的,其中q(z)叫做建议分布(proposal distribution)。
具体操作如下,设定一个方便抽样的函数q(z),以及一个常量k,使得![]() 总在kq(z)的下方,如上图所示。
总在kq(z)的下方,如上图所示。
- 给定目标分布密度
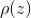
- 建议密度q(z)和常数k,使得
- 对q(z)采样比较容易
- q(z)的形状接近
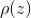 ,且有
,且有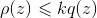
- 通过对q(z)的采样实现对
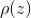 的采样
的采样 - 采样过程为:
- 产生样本
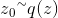 ,和
,和![U\sim Uniform[0,1]](http://img.e-com-net.com/image/info8/4a89a99ea45c4f01a2b6a22c8cc0e1f5.gif)
- 若
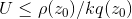 ,则接收
,则接收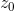
- 产生样本
- 接受的样本服从分布
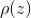 ,等价于
,等价于
- 产生样本
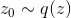 ,和
,和![U\sim Uniform[0,1]](http://img.e-com-net.com/image/info8/4a89a99ea45c4f01a2b6a22c8cc0e1f5.gif)
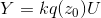 ,若
,若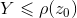 ,则接收
,则接收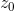
- 产生样本
虽然接受-拒绝采样比较简单,但是在高维的情况下会出现两个问题:第一是适合的q(.)分布难以找到,第二是很难确定一个合理的k值。这两个问题会导致高拒绝率,增加无用计算。
重要性采样 (Importance Sampling)
重要性采样的主要思想是通过尺度变换(Change of Measure,CM)来修改决定仿真输出结果的概率测度,使本来发生概率很小的稀有事件频繁发生,从而加快仿真速度,能够在较短时间内得到稀有事件。
用一个现有的例子说明:
一个工厂里面,工资有低,中,高三档,分别是100块,200块,300块。其中拿低档工资的工人占60%,拿中档工资的工人占30%,拿高档工资的工人占10%。求该工厂工资的期望。
一个解决方法是蒙特卡罗估计。即随机对该厂工人构造采样,求均值,结果随着采样数量增加会收敛该式
接下来,问题改变了。该工厂有一个车间,工人的收入分布有所不同:低档50%,中档30%,高档20%。假设只能从该车间工人中采样,如何得到该厂的工人工资期望。
如果我们直接从该车间工人中采样取均值,结果是错误的,因为车间工人工资分布与工厂工资分布不同,从车间工人中采样的结果应该收敛到该式
因此,我们在用来自车间的工人采样时,只需要在工人工资数额前乘上一个权重![]() ,如对于低档次工资的工人,权重为
,如对于低档次工资的工人,权重为![]() ,中档
,中档![]() ,高档
,高档![]() ,把所采工人的工资按权重求均值,就是工厂工人工资的期望值。
,把所采工人的工资按权重求均值,就是工厂工人工资的期望值。
对比两种估计:
公式一:蒙特卡罗估计,即第一种情况,从x服从p分布中采样求均值
公式二:重要性估计,即第二种情况,从x服从q分布中采样,求x服从p分布的均值
上面描述了两种从另一个分布获取指定分布的采样样本的算法,对于1)在实际工作中,一般来说我们需要sample的分布都及其复杂,不太可能求解出它的反函数,但它的值也许可以计算。对于2.找到一个适合的q往往很困难,接受概率有可能会很低。
【疑问】:对于重要性采样,我有个疑问,既然是采样,为何最后没有得到样本,反而去求均值了?
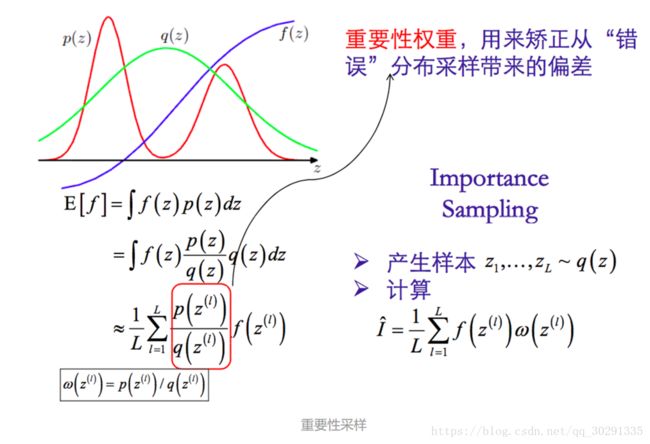
重要性采样与接受-拒绝采样有异曲同工之妙,接受-拒绝采样时通过接受拒绝方式对通过q(x)得到的样本进行筛选,使得最后的到的样本服从p(x)分布,每个接受的样本没有高低贵贱之分,一视同仁。而重要性采样的思想是,对于通过q(x)得到的样本,我全部接受!全部接受的话会有一个问题,那就是最后样本点分布不能服从p(x)分布,为了校正这个样本全部接受带来的偏差,我们给每个样本附一个重要性权重,比如,对于![]() 的样本,给的权重大一些,
的样本,给的权重大一些,![]() 的样本,给的权重小一点。
的样本,给的权重小一点。
应当注意的是,图中p(z)与f(z)的关系,p(x)是一种分布,是相对于z轴的采样点而言的,比如在红色的两个驼峰处,z的取点比较多,在其他地方z的取点比较少,这叫样本分布服从于p(z)。对于f(z)是一种映射关系,将z值映射到其他维度。比如我们熟悉的y=f(x),将x映射到y,我们所说的求均值就是求f(z)得均值。
马尔可夫链(Markov Chain)
马尔可夫链的数学定义:![]()
写不完了,日后再更