树状数组浅析
转自:http://www.cnblogs.com/frankchenfu/p/7132445.html
树状数组
动态连续和查询问题。给定一个n个元素的数组a1、a2、……,an,设计一个数据结构,支持以下两种操作:1、add(x,d):让ax增加d;2、query(l,r):计算al+al+1+…+ar
如何让query和add都能快速完成呢?方法有很多,这里介绍的便是树状数组。为此我们先介绍lowbit。
对于正整数x,我们定义lowbit(x)为x的二进制表达式中最右边的1所对应的值(而不是这个比特的序号)。比如,38288的二进制1001010110010000,所以lowbit(38288)=16(二进制是10000)。在程序中,lowbit(x)=x&-x,计算机里的整数采用补码表示,因此-x实际上是x按位取反后末尾加1的结果如下:
38288=1001010110010000
-38288=0110101001110000
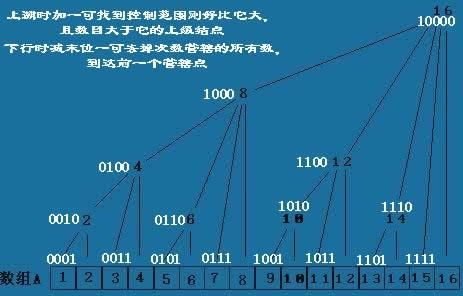
二者按位取与后,前面的部分全部变为0,之后lowbit保持不变。接下来看一张图
对于节点i,如果它是左子节点,那么他的父节点编号为i+lowbit(i);如果它是右子节点,那么父节点的编号为i-lowbit(i)。我们设辅助数组C[k]存储的是从k开始lowbit(k)个元素的和,即C[i]=A[i]+A[i-1]+…+A[i-2^k+1]。
有了以上预备知识做铺垫我们就能进行一下操作了!!
一、单点修改+区间查询
思路:假设修改第i个数即A[i],增量为num,则只需从C[i]开始往右走,沿途修改所有节点对应的C[i](即包含A[i]的区间);而求和sum(i)=A[1]+A[2]+…+A[i],则i到j的和为sum(j)-sum(i-1);
模板题:https://www.luogu.org/problem/show?pid=3374
#include
#include
#define maxn 500005
using namespace std;
int a[maxn],b[maxn],n,m; //a为原数组,b为辅助数组
inline int getint() //读入优化
{
int a=0;char x=getchar();bool f=0;
while((x<'0'||x>'9')&&x!='-')x=getchar();
if(x=='-')f=1,x=getchar();
while(x>='0'&&x<='9'){a=a*10+x-'0';x=getchar();}
return f?-a:a;
}
void update1(int k,int num) //k为需要修改第几个数,num为增量
{
while(k<=n)
{
b[k]+=num;
k+=k&-k;
}
}
int read(int k) //求和
{
int sum=0;
while(k){sum+=b[k];k-=k&-k;}
return sum;
};
int main()
{
n=getint(),m=getint();
for(int i=1;i<=n;i++){a[i]=getint();update1(i,a[i]);} //初始化b数组
while(m--)
{
int x,y,z=getint();
if(z==2){x=getint();y=getint();printf("%d\n",read(y)-read(x-1));} //区间求和
else {x=getint();y=getint();update1(x,y);} //单点修改
}
return 0;
} 二、区间修改+单点查询
思路:我们设置辅助数组C[i]=A[i]-A[i-1],容易得出第i个数为sum(i)=C[1]+C[2]+…C[i];至于区间修改,假设修改区间为[i,j]、增量k,我们只需将C[i]+k的同时C[j+1]-k即可
模板题:https://www.luogu.org/problem/show?pid=3368
#include
#include
#define maxn 500005
using namespace std;
int a[maxn],b[maxn],n,m;
inline int getint() //读入优化
{
int a=0;char x=getchar();bool f=0;
while((x<'0'||x>'9')&&x!='-')x=getchar();
if(x=='-')f=1,x=getchar();
while(x>='0'&&x<='9'){a=a*10+x-'0';x=getchar();}
return f?-a:a;
}
void update1(int k,int num) //不想多说了下面都同上一个代码的注释,主要是思路不同
{
while(k<=n)
{
b[k]+=num;
k+=k&-k;
}
}
int read(int k)
{
int sum=0;
while(k){sum+=b[k];k-=k&-k;}
return sum;
};
int main()
{
n=getint(),m=getint();
for(int i=1;i<=n;i++){a[i]=getint();update1(i,a[i]-a[i-1]);}
while(m--)
{
int x,y,z=getint(),q;
if(z==2){x=getint();printf("%d\n",read(x));}
else {x=getint();y=getint();q=getint();update1(x,q);update1(y+1,-q);}
}
return 0;
} 三、区间修改+区间查询
思路:(很有趣的数学呵呵~)设置b[i]=a[i]-a[i-1],则有等式:
a[1]+a[2]+...+a[n]
= (b[1]) + (b[1]+b[2]) + ... + (b[1]+b[2]+...+b[n])
= n*b[1] + (n-1)*b[2] +... +b[n]
= n * (b[1]+b[2]+...+b[n]) - (0*b[1]+1*b[2]+...+(n-1)*b[n])
所以我们就维护一个数组c[n],其中c[i] = (i-1)*b[i],每当修改b的时候,就同步修改一下c,这样复杂度就不会改变那么原式=n*sigma(b,n) - sigma(c,n)//sigma(b,n)表示b数组前n个数的和(时间复杂度为log2n)
模板:自己找一个(区间修改+区间查询)线段树的模板题吧!~~
#include
#include
#define maxn 100005
using namespace std;
int a[maxn],b[maxn],c[maxn],n,m;
inline int getint()
{
int a=0;char x=getchar();bool f=0;
while((x<'0'||x>'9')&&x!='-')x=getchar();
if(x=='-')f=1,x=getchar();
while(x>='0'&&x<='9'){a=a*10+x-'0';x=getchar();}
return f?-a:a;
}
void update(int *x,int k,int num)
{
while(k<=n)
{
x[k]+=num;
k+=k&-k;
}
}
int read(int *x,int k)
{
int sum=0;
while(k){sum+=x[k];k-=k&-k;}
return sum;
}
int main()
{
n=getint(),m=getint();
for(int i=1;i<=n;i++){a[i]=getint();update(b,i,a[i]-a[i-1]);update(c,i,(i-1)*(a[i]-a[i-1]));}
while(m--)
{
int x,y,z=getint(),q;
if(z==2){x=getint();y=getint();printf("%d\n",y*read(b,y)-read(c,y)-(x-1)*read(b,x-1)+read(c,x-1));}
else {x=getint();y=getint();q=getint();update(b,x,q);update(b,y+1,-q);update(c,x,q*(x-1));update(c,y+1,-q*y);}
}
return 0;
} 四、求逆序数对
思路:了解离散化,它是一种常用的技巧,有时数据范围太大,可以用来放缩到我们能处理的范围,必要的是建立一个结构体a[n],v表示输入的值,order表示原i值,再用一个数组aa[n]存储离散化后的值
例如:
i:1 2 3 4 5
v: 9 0 1 5 4
排序后:0 1 4 5 9
order:2 3 5 4 1 如果建立映射:aa[a[i].order]=i;
aa:5 1 2 4 3
即原本的9经过排序应该在第5位,现在aa[1]=5,对应原来的9,大小次序不变,只是将9缩小到了5 那么离散化之后怎么求逆序对呢?说实在的我这里想了很久,首先是通过update函数插入一个数,比如update(2,1),一开始都c[n]为0,插入后+1
,现在其余的为0,c[2],c[4]=1,这就说明前面下标为2出有一个数2,这里是关键,c[4]=1不代表下标为4时有一个数4,它的意思是在4之前的区间内所有元素之和是1,即有一个数2,具体的可以看看树状图
然后只有用getsum实时求出插入一个数的前面有几个数,就可以算出当前小于这个数的数的个数,再通过下标i-getsum(aa[i]),得到大于它的数目,即为逆序数。
模板:POJ2299
#include
#include
#include
#include
#include
using namespace std;
const int maxn= 500005;
int aa[maxn];//离散化后的数组
int c[maxn]; //树状数组
int n;
struct Node
{
int v;
int order;
}a[maxn];
bool cmp(Node a, Node b)
{
return a.v < b.v;
}
int lowbit(int k)
{
return k&(-k); //基本的lowbit函数
}
void update(int t, int value)
{ //即一开始都为0,一个个往上加(+1),
int i;
for (i = t; i <= n; i += lowbit(i))
c[i] += value;
}
int getsum(int t)
{ //即就是求和函数,求前面和多少就是小于它的个数
int i, sum = 0;
for (i = t; i >= 1; i -= lowbit(i))
sum += c[i];
return sum;
}
int main()
{
int i;
while (scanf("%d", &n), n)
{
for (i = 1; i <= n; i++) //离散化
{
scanf("%d", &a[i].v);
a[i].order = i;
}
sort(a + 1, a + n + 1,cmp);//从1到n排序,cmp容易忘
memset(c, 0, sizeof(c));
for (i = 1; i <= n; i++)
aa[a[i].order] = i;
long long ans = 0;
for (i = 1; i <= n; i++)
{
update(aa[i], 1);
ans += i - getsum(aa[i]); //减去小于的数即为大于的数即为逆序数
}
printf("%lld\n", ans);
}
return 0;
} 五、区间最大值
思路:自己yy吧,有点像倍增~~
inline void init()
{
CLR(arr,0);
for(int i=1;i<=N;++i)
for(int j=i;j<=N&&arr[j]=L){res=max(res,arr[R]);R-=lowbit(R);}
else{res=max(res,num[R]);--R;}
}
return res;
}
inline void update(int x,int val)
{
int ori=num[x];
num[x]=val;
if(val>=ori)
for(int i=x;i<=N&&arr[i]>1;j;j>>=1)
arr[i]=max(arr[i],arr[i-j]);
}
}
}