机器学习:贝叶斯公式的理解及运用—图书分类
一、贝叶斯公式
贝叶斯定理是关于随机事件A和事件B的条件概率的一个定理。
解决问题:已知B1,B2,…,Bn互斥且构成一个完全事件且已知它们的概率P(B1),P(B2)…P(Bn)。现观察到某事件A与B1,B2…Bn相伴出现,且已知条件概率P(A|Bi)求P(Bi|A)。
条件概率公式
P(A|B) : 指事件A在事件B发生的条件下发生的概率,读作“A在B发生的条件下发生的概率”。
若只有 A/B两个事件,那么P(A|B)=P(AB)/P(B)
联合概率
P(AB):指两个时间共同发生的概率
表示方式:P(A|B)/P(A,B)/P(A∩B)
边缘概率
P(A)/P(B) :指某个事件发生的概率,与其他事件无关。
边缘化:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率)。
A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
全概率公式
定义:完备事件组/样本空间的划分
设B1,B2…Bn是一组事件,若
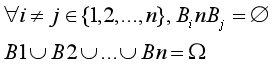
称B1,B2,…Bn是样本空间Ω的一个划分或称为样本空间Ω的一个完备事件组。
公式:满足如上条件且P(Bi)>0( i=1,2,…,n)
则对任一事件B,有
![]()
贝叶斯公式
设B1,B2,…Bn是一完备事件组,则对任一事件A, P(A)>0,有
![]()
源自百度百科
二、实例运用
1.吸毒者检测:
- 假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(+)的概率为99%。而被检者不吸毒时,每次检测呈阴性(-)的概率为99%。
- 假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。
- 解决的问题是:每位医学检测呈阳性的雇员吸毒概率有多高?令‘A’为雇员吸毒事件,‘B’为雇员不吸毒事件,‘+’为检测呈阳性事件
依题意得:
P(A)=0.005 (雇员吸毒)
P(B)=0.995 (雇员不吸毒,也就是1-P(A))
P(+|A)=0.99 (吸毒者阳性检出率,准确率为99%)
P(+|B)=0.01 (不吸毒者阳性检出率,1-P(+|A))
P(+)为不考虑其他因素的阳性检出率
P(+)=P(+A)+P(+B)=P(A)P(+|A)+P(B)P(+|B)=0.0149
综上所述,可以计算出某人检测呈阳性时确实吸毒的概率P(A|+)
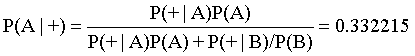
- 尽管我们的检测结果可靠性很高,但是只能得出如下结论:如果某人检测呈阳性,那么此人是吸毒的概率只有大 约33%,也就是说此人不吸毒的可能性比较大。我们测试的条件(本例中指A,雇员吸毒)越难发生,发生误判的可能性越大。
- 但如果让此人再次复检(相当于P(A)=33.2215%,为吸毒者概率,替换了原先的0.5%),再使用贝叶斯定理计算,将会得到此人吸毒的概率为98.01%。但这还不是贝叶斯定理最强的地方,如果让此人再次复检,再重复使用贝叶斯定理计算,会得到此人吸毒的概率为99.98%(99.9794951%)已经超过了检测的可靠度。
2.图书分类
判断一本书是哪一类:哲学、社科、自然科学、综合
(1)假设每本书都有如下15个标签:政治,经济,文化,心理,经典,校园,小说,青春,爱情,科学,社会,自然,游记,理论,导论
给定训练集合 哲学 :社科 :自然科学 :综合 =2:3:3:2
所以这本书属于哲学类的概率为P(H)=0.2
属于社科类的概率为P(S)=0.3
属于自然科学类的概率为P(N)=0.3
属于综合类的概率为P©=0.2
(2)以哲学类为例,给出6本哲学书的标签:
static int[][] MH=new int[][]{
//哲学6
{1,1,1,1,0,0,0,0,0,0,1,0,0,0,0},
{0,0,1,0,1,0,0,1,0,0,1,0,0,0,0},
{0,1,1,1,0,0,0,0,0,0,1,0,0,0,0},
{1,0,1,1,1,0,0,0,0,0,0,0,0,0,0},
{1,1,1,0,0,0,0,1,1,0,0,0,0,0,0},
{0,1,1,1,0,0,0,0,0,0,0,1,0,0,0}
};
(3)在MH中统计所有标签出现的总数total,计算每个标签比如“政治”出现的次数 P(政治|MH)=3/26。用这种方法求出每个标签出现在训练集中的概率得出一个数组PMtags{3/26,4/26…,1/26…},再用P(H)(哲学书在总样本中出现的概率)乘上每一项
(4)设我们要判断那本书的tags为P(B),根据3的方法求出其他分类的图书在样本中的概率,可以记为P(BH),P(BS),P(BN),P(BC)那么这本书P(B)是哲学书的概率就可以写成
P(H|B)=P(BH)/P(B)
其他图书分类的概率也用这种方法求出
(5)最后得出4个概率分别是这本书是哲学类的概率P(H|B),是社科类的概率P(H|S),自然类的概率P(H|N),是综合类的概率P(H|C)。这四个概率中的最大值就是这本图书所属分类。
代码流程图:
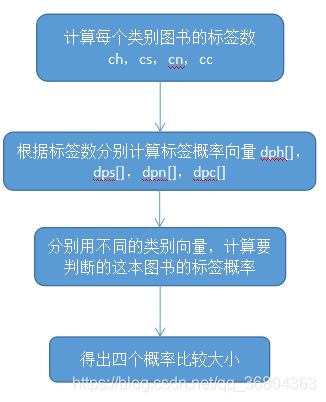
注意计算当前图书标签概率是用四个不同类别的dp[]向量来计算:
//计算这本书的标签概率
public static double newBook(int [] book, double []dp){
double pt=1.0;
for(int i=0;i<dp.length;i++){
if(book[i]>0){
pt*=dp[i];
}
}
return pt;
}
完整代码:
package ClassifyBook;
import java.util.*;
public class Classify {
static double pHil=0.2;//哲学类
static double pSoc=0.3;//社科类
static double pNat=0.3;//自然科学类
static double pCom=0.2;//综合类
//targe分类:政治,经济,文化,心理,经典,校园,小说,青春,爱情,科学,社会,自然,游记,理论,导论 (15)
static int[][] MH=new int[][]{
//哲学6
{1,1,1,1,0,0,0,0,0,0,1,0,0,0,0},
{0,0,1,0,1,0,0,1,0,0,1,0,0,0,0},
{0,1,1,1,0,0,0,0,0,0,1,0,0,0,0},
{1,0,1,1,1,0,0,0,0,0,0,0,0,0,0},
{1,1,1,0,0,0,0,1,1,0,0,0,0,0,0},
{0,1,1,1,0,0,0,0,0,0,0,1,0,0,0}
};
static int [][]MS=new int[][]{
//社科9
{0,1,1,1,1,1,1,1,1,0,1,0,0,0,1},
{0,0,1,1,1,1,1,0,0,0,1,0,0,0,0},
{0,0,0,1,0,1,1,1,0,1,0,0,0,0,0},
{0,1,1,1,0,0,0,0,0,0,1,0,0,1,1},
{0,0,1,1,0,1,0,1,0,0,1,0,0,0,0},
{0,0,0,1,1,0,1,0,1,1,0,0,0,1,1},
{0,0,1,1,0,0,1,1,1,0,1,0,0,1,0},
{0,0,0,1,0,1,0,1,0,1,1,0,0,0,0},
{0,0,0,0,0,0,1,1,1,1,0,0,0,0,1}
};
static int [][]MN=new int[][]{
//自然科学9
{0,0,1,0,0,0,1,0,0,1,1,1,1,1,1},
{0,0,0,0,1,0,0,0,0,1,0,1,1,1,0},
{0,0,0,0,1,0,0,0,0,0,0,1,1,0,0},
{0,1,1,0,0,0,0,0,0,1,1,1,1,0,0},
{0,0,0,1,0,0,0,0,0,1,0,1,0,1,0},
{0,1,0,0,1,0,0,0,0,0,0,1,1,0,0},
{0,0,1,0,0,0,0,0,0,1,0,1,1,0,0},
{0,0,0,1,0,0,0,0,0,0,1,1,0,1,0},
{0,0,0,0,0,0,0,0,0,0,1,1,1,1,1}
};
static int [][]MC=new int[][]{
//综合6
{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
{0,1,0,1,0,0,1,1,0,0,1,0,1,0,0},
{1,0,0,1,0,1,0,1,0,0,0,1,0,1,0},
{0,0,0,1,0,1,0,1,0,1,0,0,1,0,1},
{1,1,0,0,1,0,0,0,1,0,0,1,0,1,0},
{0,0,1,0,0,1,0,0,0,0,1,0,0,0,0}
};
public static void main(String []args){
//计算各个target总和
int ch=countM(MH);
int cs=countM(MS);
int cn=countM(MN);
int cc=countM(MC);
System.out.println("哲学:"+ch+" 社科:"+cs+" 自然科学:"+cn+" 综合:"+cc);
//计算各个矩阵的标签概率
double []dph=target(MH,ch);
double []dps=target(MS,cs);
double []dpn=target(MN,cn);
double []dpc=target(MC,cc);
int []book=new int[15];
Scanner in=new Scanner(System.in);
while(true){
System.out.println("请输入这本书的标签:政治,经济,文化,心理,经典,校园,小说,青春,爱情,科学,社会,自然,游记,理论,导论(0代表没有1代表有,空格隔开):");
for(int i=0;i<15;i++){
book[i]=in.nextInt();
}
//MyArrayList result=new MyArrayList();
double r1=newBook(book, dph)*pHil;
double r2=newBook(book, dps)*pSoc;
double r3=newBook(book, dpn)*pNat;
double r4=newBook(book, dpc)*pCom;
double result=Math.max(Math.max(r1, r2), Math.max(r3, r4));
if(result==r1)
System.out.println("这本书属于哲学类");
else if(result==r2)
System.out.println("这本书属于社科类");
else if(result==r3)
System.out.println("这本书属于自然科学类");
else if(result==r4)
System.out.println("这本书属于综合类");
}
}
//计算这本书的标签概率
public static double newBook(int [] book, double []dp){
double pt=1.0;
for(int i=0;i<dp.length;i++){
if(book[i]>0){
pt*=dp[i];
}
}
return pt;
}
/**
* 计算每个的标签概率
* @param a
* @param total
* @return
*/
public static double[] target(int [][]a,double total){
double []result=new double[a[0].length];
for(int i=0;i<a[0].length;i++){
float count=0;
for(int j=0;j<a.length;j++)
count+=a[j][i];
//计算每一列标签数
result[i]=count/total;
}
return result;
}
/**
* 计算数组中1出现的次数,标签总数
* @param a
* @return
*/
public static int countM(int [][]a){
int count=0;
for(int i=0;i<a.length;i++){
for(int j=0;j<a[0].length ;j++){
if(a[i][j]==1)
count++;
}
}
return count;
}
}