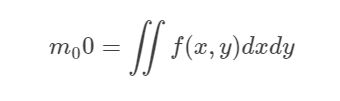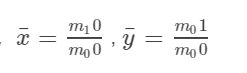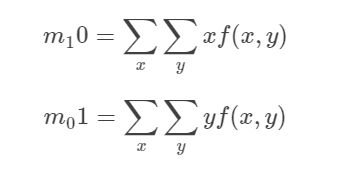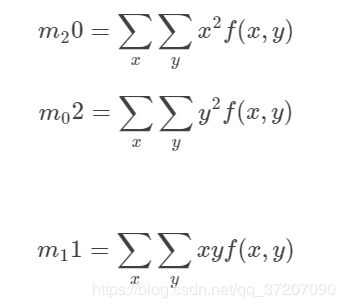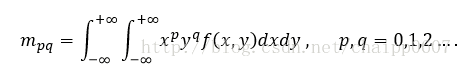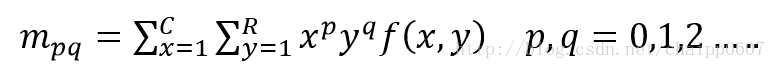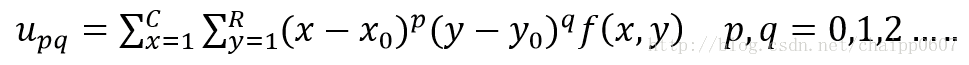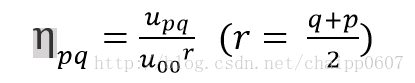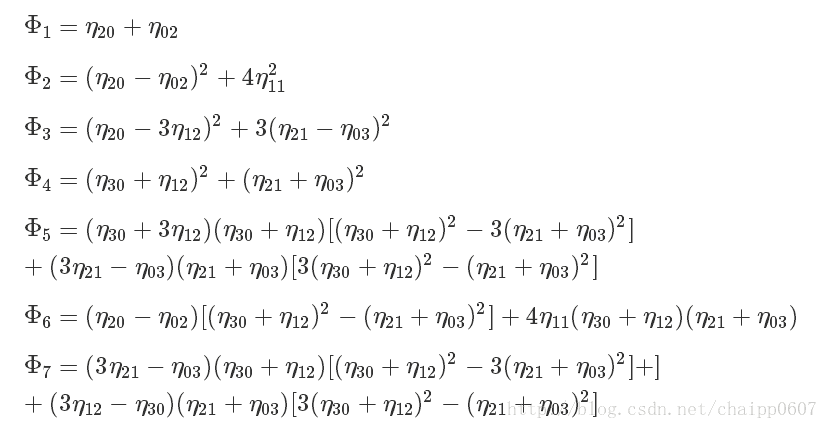图像矩（Hu矩）简介

（1）零阶矩 

根据矩的定义，二维图像的灰度用f(x,y)表示，零阶矩m00表示为：

                                 

表示的是图像灰度的总和。

 
（2）一阶矩 

图像的一阶矩m10和m01表示用来确定图像的灰度中心，

根据中心矩的定义很容易计算出，u10=0,u01=0

                                       

可以根据该公式编写matlab程序。 

(3）二阶矩 

二阶矩有三个，m11 m02 m20，也成为惯性矩。它们可以确定物体的几个特性： 
1.二阶中心矩用来确定目标物体的主轴，长轴和短轴分别对应最大和最小的二阶中心矩。可以计算主轴方向角。 
2.图像椭圆：由一阶、二阶矩可以确定一个与原图像惯性等价的图像椭圆。所谓图像椭圆是一个与原图像的二阶矩及原图像的灰度总和均相等的均匀椭圆。使得主轴与图像的主轴方向重合，一边分析图像性质。 

                                             

(4)三阶矩及以上 

对于三阶或三阶以上矩,使用图像在轴或轴上的投影比使用图像本身的描述更方便。 
三阶矩：投影扭曲，描述了图像投影的扭曲程度。扭曲是一个经典统计量,用来衡量关于均值对称分布的偏差程度。 
四阶矩：投影峰度，峰度是一个用来测量分布峰度的经典统计量。可以计算峰度系数。当峰度系数为0时,表示高斯分布；当峰度系数小于0时,表示平坦的少峰分布；当峰度系数大于0时,表示狭窄的多峰分布。

（5）Hu矩

图像的hu矩是一种具有平移、旋转和尺度不变性的图像特征。

普通矩的计算： （对上面的普通矩阵进行总结）
f(x,y)的p+q阶原点矩可以表示为： 

而数字图像是一个二维的离散信号，对上述公式进行离散化之后：

 

其中C与R分别表示图像的列与行。

 

各阶矩的物理意义： 

普通矩：
0阶矩（m00）:目标区域的质量 
1阶矩（m01,m10）：目标区域的质心 
2阶矩（m02,m11,m20）：目标区域的旋转半径 
3阶矩（m03,m12,m21,m30）：目标区域的方位和斜度，反应目标的扭曲

但是目标区域往往伴随着空间变换（平移，尺度，旋转），所以需要在普通矩的基础上构造出具备不变性的矩组—hu矩。

中心矩：构造平移不变性 
由零阶原点矩和一阶原点矩，我们可以求得目标区域的质心坐标： 
                        
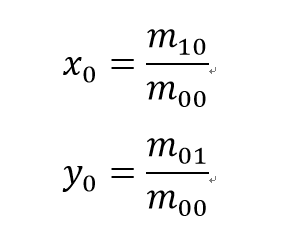
由求得的质心坐标，我们可以构造出中心矩：

       

由于我们选择了以目标区域的质心为中心构建中心矩，那么矩的计算时永远是目标区域中的点相对于目标区域的质心，而与目标区域的位置无关，及具备了平移不变性。

 

归一化中心矩：构造尺度不变性

为抵消尺度变化对中心矩的影响，利用零阶中心矩u00对各阶中心距进行归一化处理，得到归一化中心矩：

                         

由上文可知，零阶矩表示目标区域的质量（面积），那么如果目标区域的尺度发生变化（缩小2倍），显然其零阶中心矩也会相应变小，使得矩具备尺度不变性。

hu矩：构造旋转不变性 
利用二阶和三阶规格中心矩可以导出下面7个不变矩组(Φ1 Φ7)，它们在图像平移、旋转和比例变化时保持不变。 

 

参考内容：https://blog.csdn.net/tingxie9116/article/details/52582912

                 https://blog.csdn.net/chaipp0607/article/details/70256892