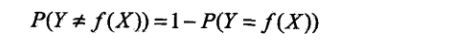K-近邻算法数学分析

K-近邻算法数学分析

前言：网上有很多关于k-近邻算法，也就是knn算法的教程和代码实现，你也可以依照很多博主的代码顺利运行算法并得到比较良好的结果，但很多教程把重点都放在了代码解析上而对其数学原理只是一笔带过，以至很多人只知其果，不知其因，笔者接下来就根据k临近算法背后的原理进行分析，包括其分类决策规则以及kd树等等

1.准备工作

笔者认为只要你具有高中以上的数学知识或者一台可以上网的笔记本，你会很轻松的理解接下来的数学分析，我们首先来温习一下knn算法的数学代码，接下来我们讨论knn的模型以及要素

2.knn算法实现

输入：输入训练集

上述训练集X是样本的特征向量，Y是样本的类别，T是一个特征空间，包含输入的样本

输出：X 所属的类别 y

（1）根据给定的距离度量，在训练集T中找出与x最邻近的k个点，包含这k个点的x的邻域记作N(k)，这里不要纠结邻域是什么，简单来说，邻域就是x点组成的集合域

（2）在N(k)中根据分类决策规则（如多数表决）决定x的类别y，其公式如下：

注意，这里I为指示函数，简答一点说，就是当括号等式成立时I为1，否则为0

之前的最邻近算法就是当k=1时的一种特殊情况，由上式我们可以很清楚的看到在k个点中，哪种类别的x个数越多，y值就是这种x对应的y类，这是非常清楚而明了的，所以，说到这里，我们已经大体了解的其数学原理了，很简单，对吧？

3.knn模型

我们一般解决问题的时候总会建立一个模型来进行分析，模型能让我们从多方面角度去直观的感受问题的关键，knn使用的模型实际上对应于对特征空间的划分，它有算法基本要素：

*距离度量

*K值选择

*分类决策规则

在knn算法中，如果上面三个要素被确定，那么你输入的任意实例，其结果也是唯一确定的，现在来介绍一下单元，单元是指在特征空间中，对每个训练实例x，距离该点比其他点更近的所有点组成的一个区域。每个实例对应一个单元，而最邻近算法将实例x的类作为其单元所有点的类标记。上面的话有点拗口，不过下面我展示的图你可以非常清晰的了解单元以及特征空间

注意，为了简单起见，这里的图是二维的，当映射到多维空间时，我们就要使用一些手段进行降维，例如使用PCA简化数据，或者SVD矩阵分解，记住，数据的优化在机器学习方面尤其重要，即使你有个表现非常完美的算法，但当数据足够大并且掺杂着许多无用或者噪声数据时，数据优化是必须进行的，上面的优化方法我会在以后的算法解析以及深度学习中进行讲解。

4.距离求解

距离这一块是非常简单的，因为具有良好性质可选择的距离类型就那么几种，一般我们使用欧式距离，或者Lp距离，由于公式编辑有点麻烦，我就直接用一张图片显示几种距离的计算：

注意，这里x你可以当做向量，以上的几种距离求解方式实质上是求解两个向量的差的模，也就是向量之间的集合距离，加上不同的幂次，构成了许多距离计算方法。

我们一般在机器学习中使用的是欧式距离，因为它具有比较良好的性质，运用python的numPy函数库进行矩阵运算是是比较方便的。

5.K的取值

首先我们要意识到，k的取值对结果会有很大的影响。

当k值取得较小时，我们就在较小的邻域的训练实例中进行的预测，这样，显而易见，输入较近的实例对预测结果会产生良好的效果，也就是其学习的近似误差会减小，但这样会让结果对这个较小邻域中的点会非常敏感，也就是说其估计误差会变大，举个栗子，如果在这小范围的邻域内恰巧有一两个噪声数据，那么你的预测结果很可能会出错，这也就是我们在线性回归中的过拟合现象

那么你可能要问，那么我把k值取得大一点，这样就可以避免噪声数据的吧！想法是好的，你这样确实会减少学习的估计误差，但学习的近似误差会增大，也就是说较远的，相关性不强的点也会产生影响，这也就是我们在线性回归中的欠拟合现象

综上所述，我们可以看到k值得取决决定你的算法效果的好坏，不过在一般应用中，k值取得是较小的数值，通常采用较差验证法来选取最优的k值

6.分类决策

在knn算法中分类决策规则往往是多数表决，也就是输入实例的k个临近的训练实例中的多数类决定输入实例的类，也就是在k个圈子中，少数人得听从多数人的决定，人多力量大，我们可以这样解释：

分类损失函数为0-1损失函数，分类函数为：

误分类的概率为：

设最邻近的k个训练实例点构成集合N(x)，则误差率公式为：

上面的公式很简单，即我们要使误分类率（有的书也叫做经验风险）最小，就是上式的最后一项最大，也就是相应的类数目越多。

7.总结

如果你首先读的是这篇博文，而且你是刚接触knn算法，读完这篇博文，你可以在我的另外一篇博文中去看看knn算法的具体实现：KNN算法改进约会网站的效果，结合上面的代码，你可以有更深的了解

8.其他

如果需要源码的话，可以在我的github上download一下，我的Github

需要相应的书籍也可以给我留言或者发我邮箱，我会帮助你

参考文献：（李航）统计学习方法

转自https://blog.csdn.net/weixin_37669436/article/details/71083327