机器学习实战--朴素贝叶斯算法应用及实例:利用贝叶斯分类器过滤垃圾邮件
声明
本文参考了《机器学习实战》书中代码,结合该书讲解,并加之自己的理解和阐述
机器学习实战系列博文
- 机器学习实战--k近邻算法改进约会网站的配对效果
- 机器学习实战--决策树的构建、画图与实例:预测隐形眼镜类型
- 机器学习实战--朴素贝叶斯算法应用及实例:利用贝叶斯分类器过滤垃圾邮件
- 机器学习实战--Logistic回归与实例:从疝病症预测病马的死亡率
朴素贝叶斯定义
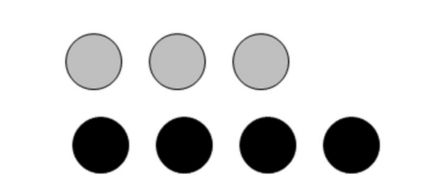
假设现在有一个装了7块石头的罐子,其中3块是灰色的, 4块是黑色的。如果从罐子中随机取出一块石头,那么是灰色石头的可能性是多少?由于取石头有7种可能,其中3种为灰色,所以取出灰色石头的概率为3/7。那么取到黑色石头的概率又是多少呢?很显然,是4/7。我们使用P(gray)来表示取到灰色石头的概率,其概率值可以通过灰色石头数目除以总的石头数目来得到。
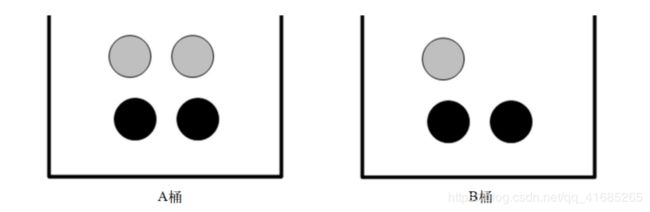
如果这7块石头放在两个桶中,那么上述概率应该如何计算?
要计算P(gray)或者P(black),事先得知道石头所在桶的信息会不会改变结果?你有可能已经想到计算从B桶中取到灰色石头的概率的办法,这就是所谓的条件概率( conditionalprobability)。假定计算的是从B桶取到灰色石头的概率,这个概率可以记作P(gray|bucketB),我们称之为“在已知石头出自B桶的条件下, 取出灰色石头的概率”。不难得到, P(gray|bucketA)值为2/4, P(gray|bucketB) 的值为1/3。
贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知P(x|c),要求P(c|x),那么可以使用下面的计算方法:
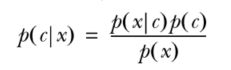
使用朴素贝叶斯进行文档分类
机器学习的一个重要应用就是文档的自动分类。在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征,下边我们就用一些已经预先分好类的文档进行朴素贝叶斯分类器的训练,然后对于未知的信息进行预分类。
构建训练数据
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1] #1 is abusive, 0 not
return postingList,classVecpostingList是一个包含词的矩阵,每一行是一个句子,也可以称为文档,classVec中第i个数值代表上边矩阵第i行是否带有侮辱性语言,1代表有,0代表没有。
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document)
return list(vocabSet)这里创建了一个set,将所有词放入set集合中,统计词的种类个数
def setOfWords2Vec(vocabList,inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec这里将所有文档转换成有0和1组成的向量
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = np.zeros(numWords); p1Num = np.zeros(numWords)
p0Denom = 0.0; p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
return p0Vect,p1Vect,pAbusive代码函数中的输入参数为文档矩阵trainMatrix,以及由每篇文档类别标签所构成的向量trainCategory。首先,计算文档属于侮辱性文档( class=1)的概率,即P(1)。计算p(wi|c1) 和p(wi|c0),需要初始化程序中的分子变量和分母变量 。由于w中元素如此众多,因此可以使用NumPy数组快速计算这些值。上述程序中的分母变量是一个元素个数等于词汇表大小的NumPy数组。在for循环中,要遍历训练集trainMatrix中的所有文档。一旦某个词语(侮辱性或正常词语)在某一文档中出现,则该词对应的个数( p1Num或者p0Num)就加1,而且在所有的文档中,该文档的总词数也相应加1 。对于两个类别都要进行同样的计算处理。最后,对每个元素除以该类别中的总词数。
利用贝叶斯分类器对文档进行分类时,要计算多个概率的乘积以获得文档属于某个类别的概率,即计算p(w0|1)p(w1|1)p(w2|1)。如果其中一个概率值为0,那么最后的乘积也为0。为降低这种影响,可以将所有词的出现数初始化为1,并将分母初始化为2,另外可对概率取对数,这样可以化乘为加。
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = np.ones(numWords); p1Num = np.ones(numWords)
p0Denom = 2.0; p1Denom = 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = np.log(p1Num/p1Denom)
p0Vect = np.log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive到这里数据就做好了,下边构建分类器
构建贝叶斯分类器
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1) # element-wise mult
p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0分类器很简单,按照贝叶斯公式直接计算就可以了。
检验分类器
def testingNB():
listOPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat = []
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = trainNB0(np.array(trainMat), np.array(listClasses))
testEntry = ['love', 'my', 'dalmation']
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
testEntry = ['stupid', 'garbage']
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))使用两组数据对分类器进行检验,检验结果如下:
['love', 'my', 'dalmation'] classified as: 0
['stupid', 'garbage'] classified as: 1
目前为止,我们将每个词的出现与否作为一个特征,这可以被描述为词集模型( set-of-wordsmodel)。如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法被称为词袋模型( bag-of-words model)。在词袋中,每个单词可以出现多次,而在词集中,每个词只能出现一次。为适应词袋模型,需要对函数setOfWords2Vec()稍加修改,修改后的函数称为bagOfWords2Vec()
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec
示例:使用朴素贝叶斯过滤垃圾邮件
划分邮件
def textParse(bigString): #input is big string, #output is word list
regEx = re.compile('\\W')
listOfTokens = regEx.split(bigString)
return [tok.lower() for tok in listOfTokens if len(tok) > 2]这里使用正则表达式划分字符串
邮件分类
def spamTest():
docList=[]; classList = []; fullText =[]
for i in range(1,26):
wordList = textParse(open("./email/spam/%d.txt" % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(1)
wordList = textParse(open('./email/ham/%d.txt' % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)#create vocabulary
trainingSet = list(range(50)); testSet=[] #create test set
for i in range(10):
randIndex = int(random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]; trainClasses = []
for docIndex in trainingSet:#train the classifier (get probs) trainNB0
trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V,p1V,pSpam = trainNB0(np.array(trainMat),np.array(trainClasses))
errorCount = 0
for docIndex in testSet: #classify the remaining items
wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
if classifyNB(np.array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
errorCount += 1
print("classification error",docList[docIndex])
print('the error rate is: ',float(errorCount)/len(testSet))最后的结果为:
classification error ['yeah', 'ready', 'may', 'not', 'here', 'because', 'jar', 'jar', 'has', 'plane', 'tickets', 'germany', 'for']
the error rate is: 0.1
说明选取的十封邮件划分正确率达到90%