小L的算法课堂：图论界的黑白无常：DFS&BFS

来自我的Blog

---

前置知识：图&树
前置知识：队列，感谢XZDXRZ大佬

---

可爱的我又双㕛叒叕来了
我们在讲解过图与树，这次我们来讨论一下，如果将图和树“跑”一趟
什么叫做“跑”呢？简单的说，就是从上到下从左到右有顺序的检查/看/遍历一次
不过，如果你想把图和树跑一边，你首先要知道他们是怎么储存在数组里边的
今天，我们暂时只讨论图的遍历

储存在数组里的图

大家肯定很快就能反应过来，这是一个典型的无向图

首先，我们用这个方式来表达两点与线的关系：

点a 点b 长度c

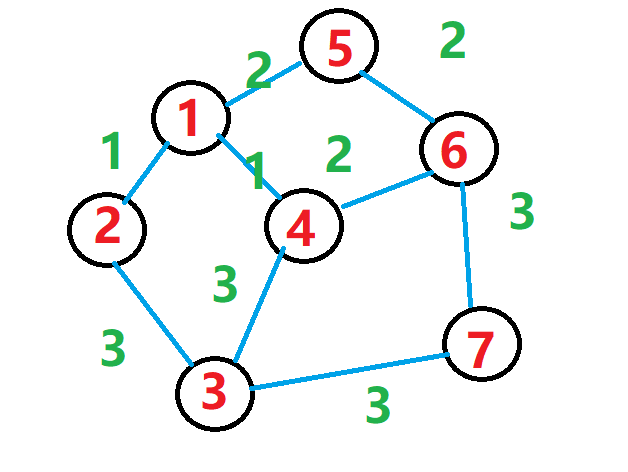
那么，这个图就可以这么表示：

1 2 1
1 5 2
1 4 1
2 3 3
5 6 2
3 4 3
6 4 2
3 7 3
6 7 3

很简单是吧
也许，你会想起用二维矩阵来存储这个图诶（这看起来就像一个二维矩阵）
但是，我们可不能这么就直接存进去，太乱了是不方便我们查询的哦
所以，我们采用这个方法：

0 1 2 3 4 5 6 7
1 & 1 & 1 2 & &
2 1 & 3 & & & &
3 & 3 & 3 & & 3
4 1 & 3 & & 2 &
5 2 & & & & 2 &
6 & & & 2 2 & 3
7 & & 3 & & 3 &

看懂了吗？第一行是点a，第一列是点b，(a,b)就是ab之间的长度。&表示两条点之间没有通路
这样，我们在接受数据的时候，我们就可以这么接受：

#define INF 1000000//这个数值表示“&”，正无穷的意思。实际上不用这么大，只需要比最大值大1就可以了
int a,b,c;
int a[7][7]//有7个点
memset(a,INF,sizeof(int));//可以自己百度一下memset函数，用于初始化数组
/*
memset其实等价于下面的语句
for(i=0;i<8;i++)
	for(j=0;j<8;j++)
		a[i][j]=INF;
*/
for(int i=0;i<7;i++)
{
    scanf("%d%d%d",&a,&b,&c);
    a[a][b]=c;
    a[b][a]=c;//因为这里是无向图，在二维矩阵中是正好对称的，所以要反向赋值
    		  //如果是有向图，就不用这样子了
}

因为这里我们是知道数组的边界大小的，我们才会写for(i=0;i<8;i++) for(j=0;j<8;j++)，实际上，应该是：

int a[101][101]//因为我们也不知道有多少个，随便设置一个，不要太大了
scanf("%d%d",&n,&m);//其实就是i和j
for(i=0;i<n;i++)
	for(j=0;j<m;j++)
		a[i][j]=INF;
for(int i=0;i<m;i++)//矩阵中就宽度不就高度

有些书上会在初始化写这么一句：

if(i==j)
	a[i][j]=0;

这么做是为了防止出现自环的情况（点a和点b都为自己并且长度为0或其他数值）

遍历一个图

遍历一个图的时候，我们一定要有顺序的遍历
我们最基本有两种方法
第一种特倔：你强任你强，劳资不撞南墙不回头，人称深度优先搜索，简称DFS！
哇，是不是被吓到了？我们看看第二种特搓的方法：嗯，这条路怎么样？哎呀还是回去吧！这个怎么样？哎呀还是回去吧，哦大家好，我叫广度优先搜索，人称BFS
他们俩可谓是我们搜索界的黑白无常，万能啊！兄台！
首先介绍一下黑无常DFS

DFS

我：DFS大哥，请您给我们介绍一下您吧！
DFS：好啊！首先，我是一种算法（不说你也知道）
并且，我是万能的！
我喜欢把一条路走到头，走到头了再返回找另一条路。
我的主要工作原理是 递归
我的基本模式是这样子的：

void dfs()
{
    判断边界
    尝试每一种可能 for(int i=0;i<n;i++)
    {
        do_something();
        继续走下一步dfs(step+1);
    }
    返回
}

我：哇！您真厉害，我们这里有一个图，您给我们详细讲解一下吧！
我们准备了一个简单图：

1 2 //因为不需要长度就没有写
1 3
1 5
3 5
2 4

DFS：简单的说，就是 先从一个为走到过的顶点作为启示顶点，用这个点连接的边去访问其他点 我们先从1号开始

沿1号点的边去访问其他点，找到2号店没有访问过，于是来到2号点
再以2号点为出发点继续往下走，又来到了4号点
发现4号点不能再走了，返回2号点
但是2号点也没有边能走，回到1号点
2号点走过了，所以走到3号点
再从3号点往下走，走到5号点
5号点没有路，返回3号点
3号点没有路，返回1号点
1号点没有未访问过的点了，访问结束

那么，代码长这个样子：

#include 
#define INF 1000000

int book[101],sum,n,e[101][101];

void dfs(int cur) //cur是当前点的编号
{
    printf("%d",cut);
    sum++;//每访问一个点，就把次数+1
    if(sum==n){return ;} //访问完毕就返回
    for (int i=1; i<=n;i++) //从1到n依次尝试
    {
        //判断当前顶点cur到其他顶点i是否有路可走，并且i是否被访问过
        if(e[cur][i] == 1 && book[i] ==0)
        {
            book[i]=1;//标记顶点访问过
            dfs(i);//从i顶点（当前顶点）继续遍历
        }
    }
    return ;
}
int main()
{
    int m,a,b;
    scanf("%d%d",&n,&m);
    
    //初始化，采用第二种
    for(int i=0;i<8;i++)
		for(int j=0;j<8;j++)
            if(i==j)	e[i][j]=0;
		   else e[i][j]=INF;
    //读入
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&a,&b);
        e[a][b]=1;//因为没有读入边长，所以就设为1，没有边长的时候可以用bool数组来解决
        e[b][a]=1;//反向赋值，一定要注意在有向图中，不要这一步
    }
    
    //从1号开始出发
    book[1]=1;//1号已经访问
    dfs(1);//1号开始遍历
    
    return 0;
}

DFS：还有，我们把每个点被访问的顺序叫做时间戳。这个程序就是让我们了解到DFS遍历图的时间戳

输入以下数据：

5 5
1 2
1 3
1 5
2 4
3 5

运行结果：

1 2 3 5 4

---

BFS

我：BFS小姐姐，你好，您能给我们介绍一下您吗？
BFS：当然可以！
我呢，做事比较犹豫，我喜欢一次多试一下。
我喜欢和队列一起工作。我每次把我试探到的路告诉队列，队列就帮我存起来
对于简单图

1 2 //因为不需要长度就没有写
1 3
1 5
3 5
2 4

我是这么遍历的：

首先，从1号顶点开始，把1号存入队列
寻找从1号出发能通向其他的点2、3、5，存入队列
接着从2开始遍历，2号点能找到4号，存入队列
回到1号，3、5号顶点都不能通向其他的未通过的顶点了，遍历结束、

我们得到的BFS解这个题目是这样子的：

#include

int main()
{
    int i, j, n, m, a, b, cur, e[101][101], book[101] = { 0 };
    int que[10001], head, tail;

    scanf_s("%d%d", &n, &m);

    //初始化二维矩阵
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (i == j)
                e[i][j] = 0;
            else 
                e[i][j] = 99999999;//假设99999999为正无穷
    //读入顶点之间的边
    for (i = 1; i <= m; i++)
    {
        scanf_s("%d%d", &a, &b);
        e[a][b] = 1;
        e[b][a] = 1; //这里是无向图，e[b][a] = 1
    }

    //队列初始化
    head = 1;
    tail = 1;

    //从1号顶点出发，将1号顶点加入队列
    que[tail] = 1;
    tail++;
    book[1] = 1; //标记1号顶点已经访问

    //当队列不为空时循环
    while (head < tail&&tail <= n)
    {
        cur = que[head];//当前正在访问的顶点编号
        for (i = 1; i <= n; i++) //从1~n依次尝试
        {
            //判断从顶点cur到顶点i是否有边，并判断顶点i是否已经访问过
            if (e[cur][i] == 1 && book[i] == 0)
            {
                //如果从顶点cur到顶点i有边，并且顶点i没有被访问过，则将顶点i入队
                que[tail] = i;
                tail++;
                book[i] = 1; //标记顶点i已经访问
            }
            if (tail>n)
                break;
        }
        head++;//head++，才能继续往下扩展
    }
    for (i = 1; i<tail; i++)
        printf(" %d ", que[i]);

    getchar(); getchar();
    return 0;
}

我：看来小姐姐的工作需要队列的支撑啊！诶，话说你和队列关系怎么样？DFS和你什么关系……（一脸八卦）
BFS,DFS,队列：你给我过来！

---

全剧，完

其实对于图论不只有遍历，最令人向往的是最短路、次短路、K短路等，还有最小生成树，割点割边，等等很多的知识，我们会一一讲解

---

原文地址