2019 ICPC Asia Yinchuan Regional(水题题解)
B. So Easy
Mr. G invents a new game whose rules are given as follows.
Firstly, he has a n \times nn×n matrix, all elements of which are 00 initially. Then, he follows up with some operations: in each time he chooses a row or a column, and adds an arbitrary positive integer to all the elements in the selected row or column. When all operations have been finished, he hides an element in the matrix and the element is modified to -1−1.
Now given the final matrix, you are asked to find out what the hidden element should be before the very last hiding operation.
Input
The first line contains a single integer n(2≤n≤1000).
Next nn lines represent the matrix after the operations. Each element in the matrix satisfies −1≤a i,j≤1000000, and exactly one element is -1.
Output
Output a single integer, the hidden element.
样例输入
3
1 2 1
0 -1 0
0 1 0
样例输出
1
题意
n×n的数值矩阵,初始数值全为 0,你可以对每一行或者每一列同时加某一正整数,得到最终矩阵,问你某一点的数值(输入是-1的点)
思路
- 找到 -1 点的位置(ai,aj),记录,并把这个点重新赋值为 0
- 先进行行操作,找每一行的最小值,再每个数都减去这个最小值,注意的是最小值寻找时,要避开(ai,aj)点
- 同理进行列操作
- 输出 -a[ai][aj]
#includeI Base 62
As we already know, base64 is a common binary-to-text encoding scheme. Here we define a special series of positional systems that represent numbers using a base (a.k.a. radix) of 2 to 62. The symbols ‘0’ – ‘9’ represent zero to nine, and ‘A’ – ‘Z’ represent ten to thirty-five, and ‘a’ – ‘z’ represent thirty-six to sixty-one. Now you need to convert some integer z in base xx into base y.
Input
The input contains three integers x, y (2≤x,y≤62) and z (0≤z
Output
Output the integer zz in base yy.
样例输入
16 2 FB
样例输出
11111011
题意
把一个 x 进制数 z 转化成 y 进制数,输出注意:0 ~ 9对应’0’ ~ 9’,10 ~ 35对应 ‘A’ ~ ‘Z’,36 ~ 61对应 ‘a’ ~ ‘z’。
思路
进制转换的模板题目:
#includeG. Pot!!

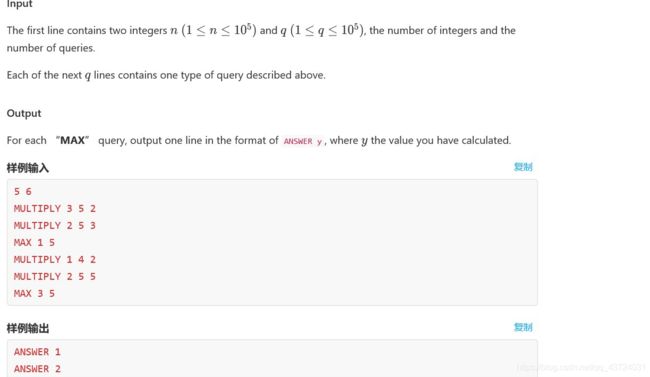
样例输入:
5 6
MULTIPLY 3 5 2
MULTIPLY 2 5 3
MAX 1 5
MULTIPLY 1 4 2
MULTIPLY 2 5 5
MAX 3 5
样例输出:
ANSWER 1
ANSWER 2
题意
给以一段 1~n 的区间(tree),他们的初始值为 1,有两个操作:
- MULTIPLY l r x 操作:让[l,r] 内的每个数乘以 x (2<=x<=10)
- MAX l r 操作:输出[l,r]的最大 m,tree[i] % pm = 0 && tree[i] % pm+1 != 0,i∈[l,r],p是任意素数。
思路
区间修改和查询问题很明显是线段树问题,这里的MAX操作像是一个质因分解操作。
打素数表,然后对每一个数质因分解??
我们想一下,x的取值范围[2,10],那么这些区间里的质因子一定是<=10的,那么就是 2 3 5 7 这四个数了
那么就线段树维护 2 3 5 7 这四个值得 mx,然后MAX是查询最大mx就行了。
#include