2018年高考数学全国卷1第16题的18般武艺

2018年高考已经结束,从全国卷1理科卷来看,出题中规中矩,覆盖知识点比较全面,难度并不是很大.若平时复习不是打酱油的话,很多基础题是没有问题的.

填空题第16题以三角函数为载体,考查求最值问题,考生可以有不同的切入角度,从而有不同的解题方法,体现出学生思维灵活性的差异,对学生可能有难度,部分学生可能会直接去化简合并,但不会成功;直接求导讨论函数的极值点会成功.

已知函数 f(x)=2sinx+sin2x, f ( x ) = 2 sin ⁡ x + sin ⁡ 2 x , 则 f(x) f ( x ) 的最小值是 _ .

01常规求导法

首先说的是常规求导法，即求出函数的导数，令导数为0，求出极值，极值与区间端点处的函数值进行比较，最大的就是最大值，最小的就是最小值，当然在具体处理时还有一些细节方面的注意，比如不可导点也应该考虑进来，有时不需要求出极值点，只需求出极值点满足的条件.

显然, f(x) f ( x ) 的周期为 2π 2 π ,所以可以在一个周期 [0,2π) [ 0 , 2 π ) 内讨论,
f′(x)=2cosx+2cos2x=2cosx+2(2cos2x−1) f ′ ( x ) = 2 cos ⁡ x + 2 cos ⁡ 2 x = 2 cos ⁡ x + 2 ( 2 cos 2 ⁡ x − 1 )

=2(2cos2x+cosx−1)=2(2cosx−1)(cosx+1) = 2 ( 2 cos 2 ⁡ x + cos ⁡ x − 1 ) = 2 ( 2 cos ⁡ x − 1 ) ( cos ⁡ x + 1 )

令 f′(x)=0, f ′ ( x ) = 0 , 得 cosx=−1, cos ⁡ x = − 1 , 或 cosx=12. cos ⁡ x = 1 2 .

在 [0,2π) [ 0 , 2 π ) 内, f(x) f ( x ) 的最小值只能在使得
cosx=1,cosx=−1,cosx=12 cos ⁡ x = 1 , cos ⁡ x = − 1 , cos ⁡ x = 1 2
的这些点处取到.对应的 sinx sin ⁡ x 的值依次是
sinx=0,sinx=0,sinx=±3–√2. sin ⁡ x = 0 , sin ⁡ x = 0 , sin ⁡ x = ± 3 2 .
显然， f(x)=2sinx+sin2x=2sinx(1+cosx) f ( x ) = 2 sin ⁡ x + sin ⁡ 2 x = 2 sin ⁡ x ( 1 + cos ⁡ x ) 的最小值为
2⋅(−3–√2)⋅(1+12)=−33–√2. 2 ⋅ ( − 3 2 ) ⋅ ( 1 + 1 2 ) = − 3 3 2 .

02均值不等式法

拿到这个题目，求导法是第一思路，除了这个思路还有其他方法吗？均值不等式也是常用的方法，但这个题目也要先变形一下.

f(x)=2sinx+sin2x=2sinx(1+cosx) f ( x ) = 2 sin ⁡ x + sin ⁡ 2 x = 2 sin ⁡ x ( 1 + cos ⁡ x )

=4sinx2cosx2(2cos2x2)=8sinx2cos3x2 = 4 sin ⁡ x 2 cos ⁡ x 2 ( 2 cos 2 ⁡ x 2 ) = 8 sin ⁡ x 2 cos 3 ⁡ x 2
记 a=sinx2,b=cosx2, a = sin ⁡ x 2 , b = cos ⁡ x 2 ,
问题转化为求 8ab3 8 a b 3 在 a2+b2=1 a 2 + b 2 = 1 条件下的最小值.

1=a2+b2=b23+b23+b23+a2 1 = a 2 + b 2 = b 2 3 + b 2 3 + b 2 3 + a 2

⩾4⋅b23⋅b23⋅b23⋅a2−−−−−−−−−−−−−√4 ⩾ 4 ⋅ b 2 3 ⋅ b 2 3 ⋅ b 2 3 ⋅ a 2 4
∴(b23)3⋅a2⩽(14)4 ∴ ( b 2 3 ) 3 ⋅ a 2 ⩽ ( 1 4 ) 4
a2b6⩽3344,ab3⩾−33–√16,min8ab3=−33–√2 a 2 b 6 ⩽ 3 3 4 4 , a b 3 ⩾ − 3 3 16 , min 8 a b 3 = − 3 3 2
其实得到不等式后，后面的可以不用算，直接看取等号条件是
b2=3a2,∴a2=14,b2=34, b 2 = 3 a 2 , ∴ a 2 = 1 4 , b 2 = 3 4 , 从而
min8ab3=−8⋅12⋅(3–√2)3=−33–√2. min 8 a b 3 = − 8 ⋅ 1 2 ⋅ ( 3 2 ) 3 = − 3 3 2 .

03琴生不等式法

如果知道琴生不等式，用它来做本题，也是不错的，但是似乎有点超纲了，不过幸亏不是解答题啦.

已知函数 f(x) f ( x ) 为奇函数,周期为 2π, 2 π ,
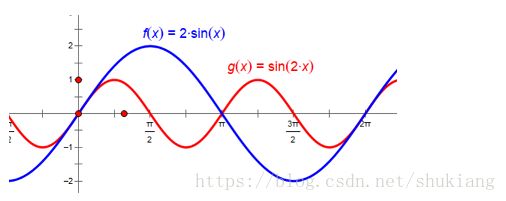
根据函数 y=2sinx y = 2 sin ⁡ x 和 y=sin2x y = sin ⁡ 2 x 图像，只需考虑函数 f(x) f ( x ) 在 [0,π2] [ 0 , π 2 ] 上的最大值.最大值的相反数就是所求最小值.

函数 sinx sin ⁡ x 在 [0,π2] [ 0 , π 2 ] 上是上凸函数，根据琴生不等式可得

f(x)=2sinx+sin2x=sinx+sinx+sin(π−2x) f ( x ) = 2 sin ⁡ x + sin ⁡ 2 x = sin ⁡ x + sin ⁡ x + sin ⁡ ( π − 2 x )

⩽3sinx+x+(π−2x)3=33–√2, ⩽ 3 sin ⁡ x + x + ( π − 2 x ) 3 = 3 3 2 ,
取等号条件为 x=π−2x, x = π − 2 x , 即 x=π3. x = π 3 .
∴minf(x)=−33–√2. ∴ min f ( x ) = − 3 3 2 .

顺便再啰嗦几句，介绍一下上凸函数和琴生不等式.

上凸函数的概念：

如果函数 f(x) f ( x ) 满足对定义域上任意两个数 x1,x2 x 1 , x 2 都有

f(x1+x22)⩾f(x1)+f(x2)2 f ( x 1 + x 2 2 ) ⩾ f ( x 1 ) + f ( x 2 ) 2

那么 f(x) f ( x ) 为上凸函数，函数图像开口向下.

琴生不等式：

如果函数 f(x) f ( x ) 是区间上的上凸函数，则对任意的 x1,x2,⋯,xn x 1 , x 2 , ⋯ , x n
f(x1+x2+⋯+xnn)⩾f(x1)+f(x2)+⋯+f(xn)n f ( x 1 + x 2 + ⋯ + x n n ) ⩾ f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) n

等号当且仅当 x1=x2=⋯=xn x 1 = x 2 = ⋯ = x n 时取得.

04几何图形法

几何图形法是我突然想到的，用来做填空题也是比较迅速的，请看.

f(x)=2sinx+sin2x=2sinx(1+cosx) f ( x ) = 2 sin ⁡ x + sin ⁡ 2 x = 2 sin ⁡ x ( 1 + cos ⁡ x )

记 a=sinx,b=1+cosx, a = sin ⁡ x , b = 1 + cos ⁡ x ,
问题转化为求 2ab 2 a b 在 a2+(b−1)2=1 a 2 + ( b − 1 ) 2 = 1 条件下的最小值.

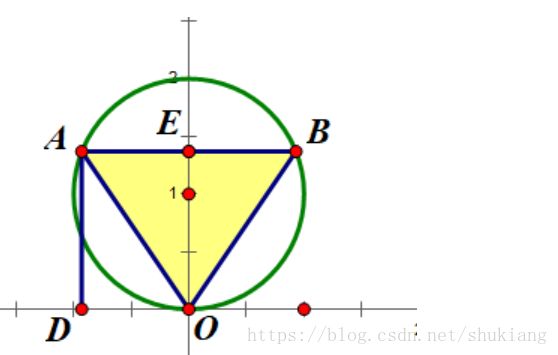
如图所示，显然符合要求的点 (a,b) ( a , b ) 在第二象限，设为 A A ，
AD⊥x A D ⊥ x 轴， AE⊥y A E ⊥ y 轴， B B 为 A A 点关于 y y 轴的对称点，
则 |ab| | a b | 为四边形 ADOE A D O E 的面积，也为三角形 AOB A O B 的面积，
根据圆的内接三角形中等边三角形面积最大，
得 |ab| | a b | 的最大值为 33–√4, 3 3 4 ,
从而 2ab 2 a b 的最小值为 −2⋅33–√4=−33–√2, − 2 ⋅ 3 3 4 = − 3 3 2 ,

我的讲解结束了，你用的是那种方法呢？请告诉我。转载是一种动力 分享是一种美德。