leetcode刷题总结（四）

2019/9/2：盛最多水的容器与三数之和

题目一链接：盛最多水的容器

题目二链接：三数之和

这两题的思想都是用双指针找到最大值或者是最合适的值，加深了我对指针的概念，另外我确实需要反复看这两题：

题一可以这么理解：由于面积取决于边长短的那一端假设为m，所以要想得到比当前更大的面积，边长短的那一端必须舍弃，因为如果不舍弃，高最大就是m，而随着指针的移动宽会一直减小，因此面积只会越来越小。

完整的一个双指针证明可以看下面链接：

双指针法正确性证明

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left = 0
        right = len(height) - 1
        maxArea = 0
        while left < right:
            b = right - left
            if height[left] < height[right]:
                h = height[left]
                left += 1
            else:
                h = height[right]
                right -= 1
            area = b*h
            if maxArea < area:
                maxArea = area
        return maxArea

题二关于三数之和暂时还没看懂，先mark一下这个老哥的：

https://leetcode-cn.com/problems/3sum/solution/3sumpai-xu-shuang-zhi-zhen-yi-dong-by-jyd/

2019/9/4：最接近的三数之和与三数之和

链接：最接近的三数之和

经过上面三数之和的洗礼，这题感觉没有那么难理解了，同样也是排序加双指针，根据下面的思路终于是写出了代码：

• 首先对数组进行排序，时间复杂度为$O(nlogn)$
• 在数组$nums$中，进行遍历， 每遍历一个值利用其下标 i，形成一个固定值nums[i]
• 再使用前指针指向$left=i+1$处，后指针指向$right=nums.lengh-1$处，也就是结尾处
• 根据$cu{r}_{s}um=nums[left]+nums[right]+nums[i]$的结果，判断cur_sum与目标target的距离，如果更近则更新结果res
• 同时判断sum与target的大小关系，因为数组有序，如果$cu{r}_{s}um>target$，则$right-=1$，如果$cu{r}_{s}um<target$，则$left+=1$，如果$cu{r}_{s}um=target$，则说明距离为0直接返回结果
• 总的时间复杂度：$O(nlogn)+O(n^2)=O(n^2)$

代码为：

class Solution(object):
    def threeSumClosest(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        nums.sort()
        res= []
        dq = float("inf")	# # 初始化，因为找最小值，因此把初始值设置成实数的最大值
        n = len(nums)
        if len(nums) < 3:
            return []
        for i in range(n-2):
            left = i + 1
            right = n - 1
            while left < right:
                cur_sum = nums[left] + nums[right] + nums[i]
                if abs(cur_sum - target) < dq:
                    dq = abs(cur_sum - target)
                    res = cur_sum
                elif cur_sum < target:
                    left += 1
                elif cur_sum > target:
                    right -= 1

                else:
                    return target
        return res

这里有一个不解的地方在于，刚开始我后面的if中，直接给abs(dq - target) > abs(cur_sum - target)，因为这个基本是肯定的，无限大的数减去一个数还是无限大，但结果报超时，嗯，不是很懂为什么，这里顺便记录一下。

三数之和

链接：https://leetcode-cn.com/problems/3sum/

再回到上一题中，大致思路为：

• 当 nums[i] > 0 时直接breai跳出：因为 $nums[right]>=nums[left]>=nums[i]>0$，即3个数字都大于0，在此固定指针i之后不可能再找到结果了。
• 当 i > 0且nums[i] == nums[i - 1]时即跳过此元素nums[i]：因为已经将 nums[i - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。
• left，right 分设在数组索引$(i,len(nums))$两端，当left < right时循环计算$cu{r}_{n}um=nums[i]+nums[left]+nums[right]$，并按照以下规则执行双指针移动：
  • 当cur_num < 0时，left += 1并跳过所有重复的nums[left]；
  • 当cur_num > 0时，right -= 1并跳过所有重复的nums[right]；
  • 当cur_num == 0时，记录组合[i, left, right]至cur_num，执行left += 1和right -= 1并跳过所有重复的nums[left]和nums[right]，防止记录到重复组合。

代码为：

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        nums.sort()
        n = len(nums)
        res = []
        #print(nums)
        for i in range(n):
            if i > 0 and nums[i] == nums[i-1]:
                continue
            left = i + 1
            right = n - 1
            while left < right:
                cur_sum = nums[i] + nums[left] + nums[right]
                if cur_sum == 0:
                    tmp = [nums[i],nums[left],nums[right]]
                    res.append(tmp)
                    while left < right and nums[left] == nums[left+1]:
                        left += 1
                    while left < right and nums[right] == nums[right-1]:
                        right -= 1
                    left += 1
                    right -= 1
                elif cur_sum > 0:
                    right -= 1
                else:
                    left += 1
        return res

2019/9/6：搜索旋转排序数组

链接：https://leetcode-cn.com/problems/search-in-rotated-sorted-array/

看了下别人的讨论，想到并发现了一种python比较好玩的思路，可以一行搞定的：

class Solution(object):
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        return nums.index(target) if target in nums else -1 

而本题应该是使用二分查找更好一点，然后我看了一下各位大佬的方法，发现这题解题方案很多，我挑了一种比较好理解的，等明天再看看：

class Solution:
    def search(self, nums, target):
        size = len(nums)
        if size == 0:
            return -1

        left = 0
        right = size - 1
        while left < right:
            # mid = left + (right - left + 1) // 2
            mid = (left + right + 1) >> 1
						
						# 右半部分有序
            if nums[mid] < nums[left]:      
                if nums[mid] <= target <= nums[right]:
                    left = mid
                else:
                    right = mid - 1
            else:
                if nums[left] <= target < nums[mid]:
                    right = mid - 1
                else:
                    left = mid
        # 后处理
        return left if nums[left] == target else -1

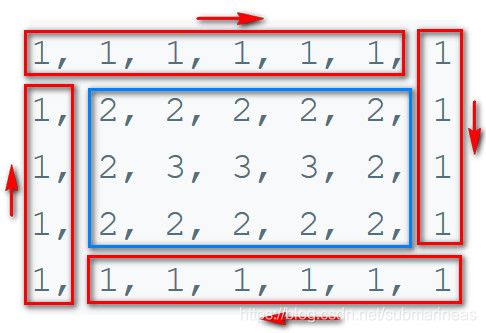
2019/9/8：螺旋矩阵

题目链接： https://leetcode-cn.com/problems/spiral-matrix/

知道了题目意思，但不知道怎么做，然后看懂了两种方法，官方的没懂，这里记录一下：

思路一，按照顺序依次相加，运用递归的方式，每一行每一列我们都留下最后一个元素，这样更加方便循环：

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix: return []
        NROW = len(matrix)
        NCOL = len(matrix[0])
        
        def helper(depth):
            nrow, ncol = NROW - 2 * depth, NCOL - 2 * depth
            if nrow <= 0 or ncol <= 0: return []
            if nrow == 1: return matrix[depth][depth:depth+ncol]
            if ncol == 1: return [matrix[r][depth] for r in range(depth, depth + nrow)]

            res = []
            res += matrix[depth][depth:depth+ncol-1]
            res += [matrix[r][depth+ncol-1] for r in range(depth, depth + nrow - 1)]
            res += reversed(matrix[depth+nrow-1][depth+1:depth+ncol])
            res += [matrix[r][depth] for r in reversed(range(depth +1, depth + nrow))]
            return res + helper(depth + 1)
            
        return helper(0)

方法二，是我看到这个题目里面最简单的一种了，这种思路是为逆时针旋转矩阵：先转置，再上下翻转。顺时针旋转矩阵：先上下翻转，再转置。

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        while matrix:
            res += matrix.pop(0)
            matrix = list(map(list, zip(*matrix)))[::-1]
        return res

2019/9/9：螺旋矩阵 II

class Solution:

    def generateMatrix(self, n: int) -> List[List[int]]:

        # 预创建矩阵
        matrix = [[0] * n for _ in range(n)]

        # 当前数值
        i = 1

        # 从最外层向最内层，逐层构造
        # 内层比外层少2个元素
        for j in range(n, 0, -2):

            # 当前层数的起始x, y
            start_x, start_y = (n - j) // 2, (n - j) // 2

            # 本次遍历起始的x, y
            x, y = 0, 0

            # 开始遍历，每层至多遍历4 * (j - 1)次
            for k in range(4 * (j - 1)):

                # 设置矩阵对应位置的值
                # 当前层的起始坐标加上遍历过程中变化的坐标，即是整个矩阵中对应的位置
                matrix[start_y + y][start_x + x] = i
                # 数值加一
                i += 1

                # 顺序填充，第一行
                if 0 <= k < j - 1:
                    # 顺序增一
                    x += 1
                # 顺序谭崇，最后一列
                elif j - 1 <= k < 2 * (j - 1):
                    # 顺序增一
                    y += 1
                # 逆序填充，最后一行
                elif 2 * (j - 1) <= k < 3 * (j - 1):
                    # 逆序增一
                    x -= 1
                # 逆序填充，第一列
                elif 3 * (j - 1) <= k < 4 * (j - 1):
                    # 逆序增一
                    y -= 1

        # 如果n为奇数，则最中间的的数仍未调整
        if n % 2:
            matrix[n // 2][n // 2] = i

        return matrix

2019/9/12：不同路径和股票的最佳投资

不同路径：https://leetcode-cn.com/problems/unique-paths/

这个题目从看到图的时候就想到应该是递归或者动态规划，所以我这里是动态规划，一般动态规划需要考虑的有两个方面，一个是初始状态，另一个是状态转移方程，如果这两个定义好了，那么最难的问题就解决了。

class Solution:
    def uniquePaths(self,m, n):
        """
            1. dp问题, dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
            2. 第一行, 第一列均为1
        """
        dp = [[0 for _ in range(n)] for _ in range(m)]	# 定义一个空的容器
        for i in range(n):	
            dp[0][i] = 1	# 横着每次只能走一步，初始状态
        for i in range(m):
            dp[i][0] = 1	# 纵轴每次只能走一步
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

        return dp[m - 1][n - 1]		# fang返回最后一个值

股票的最佳投资

题目链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/

这题依然是动态规划，我看了两篇博客的思路，其中一种方式是评论里的一句话：动态规划 前i天的最大收益 = max{前i-1天的最大收益，第i天的价格-前i-1天中的最小价格}

所以可以写出代码为：

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        maxprofit = 0
        n = len(prices)
        if n <= 1:
            return 0
        thein = prices[0]
        for i in prices:
            thein = min(i,thein)
            maxprofit = max((i- thein),maxprofit)
        return maxprofit

第二种想法是依据 一个方法团灭6道股票问题 ， 按照下面这张图，可以写出代码：

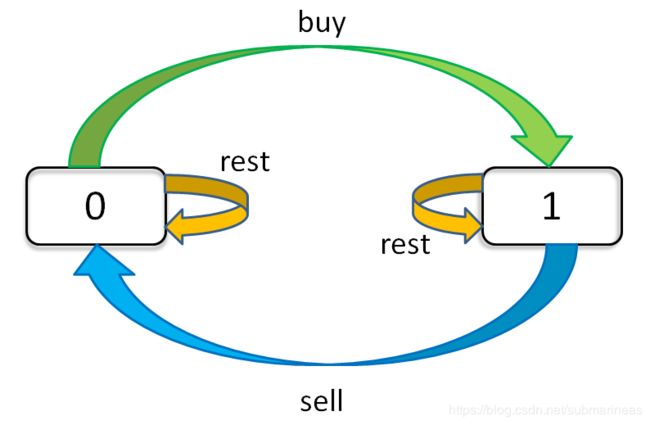
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        n = len(prices)
        if n <= 1:
            return 0

        dp = [[0] * 2 for _ in range(n)]
        print(dp)
        dp[0][0], dp[0][1] = 0, -prices[0]
        
        for i in range(1, n):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
            dp[i][1] = max(dp[i - 1][1], -prices[i])
        return dp[n - 1][0]

2019/9/13：合并两个有序数组

题目链接：https://leetcode-cn.com/problems/merge-sorted-array/

这题看完题目就可以想到的是用列表一中的0替换成列表二中的元素，不然题目中为什么要构造成一个合适列表二元素的空间，所以代码为：

class Solution(object):
    def merge(self, nums1, m, nums2, n):
        nums1[:] = sorted(nums1[:m] + nums2)

然后看了官方解，发现还能用双指针，可能这才是出题人想表达的想法吧，我之后再去看一下，另外下图中我发现了一种很神奇的现象：

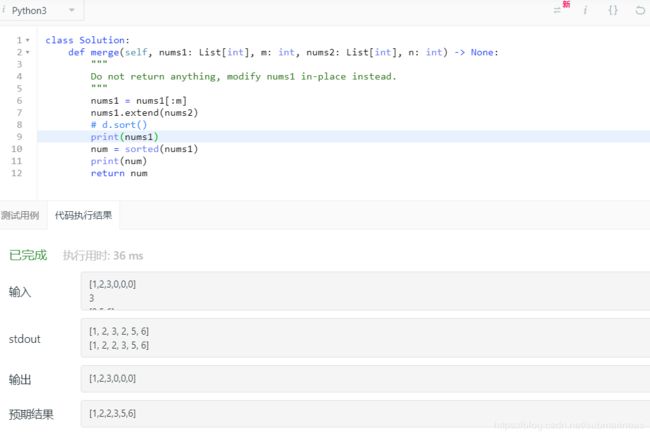
感觉这题应该是将nums1固定了，和下面这题一样。

2019/9/13：删除排序数组中的重复项 和 存在重复元素

题目链接：https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/

本题难点应该是不能额外开辟内存空间，刚开始自己是想和上面这题一样，实验一下一些内置函数和关键字，这里想要用set，虽然不知道这些有没有开辟空间，然后报错为 TypeError: [1, 2] is not valid value for the expected return type integer[]

然后看了一下大佬们的双指针，结合前面已经被双指针虐过的经验，写了一种简洁一点的：

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        prev, next = 0,1
        for i in range(1,len(nums)):
            if nums[prev] == nums[next]:
                nums.pop(next)
                i += 1
            else:
                prev,next = prev + 1,next + 1
        return len(nums)

然后还有一种双指针比这个的时间复杂度好一点，为：

class Solution:
    def removeDuplicates(self, nums: [int]) -> int:
        if not nums: return 0
        k = 1
        for i in range(1, len(nums)):
            if nums[i] != nums[i - 1]:
                nums[k] = nums[i]
                k += 1
        return k

存在重复元素

题目链接：https://leetcode-cn.com/problems/contains-duplicate/

这题基本没有难度，直接上代码为：

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        a = set(nums)
        if len(nums) <= 1:
            return False
        if len(a) != len(nums):
            return True
        else:
            return False
        
        # return len(nums) != len(set(nums))

2019/9/13：除自身以外数组的乘积

题目链接：https://leetcode-cn.com/problems/product-of-array-except-self/

思考了下想到了双指针，但经验太少，另外这题没有看出潜在的规律确实也有原因，看了下别人的代码，总结一下，这题的思路应该就是双向遍历加两个动态规划了，然后两种风格很nice的代码如下：

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        res, l, r = [1] * len(nums), 1, 1
        for i, j in zip(range(len(nums)), reversed(range(len(nums)))):	# 双向遍历
            res[i], l = res[i] * l, l * nums[i]
            res[j], r = res[j] * r, r * nums[j]
        return res

对该数组进行二维展开，形成一个矩阵，然后再对每个元素进行相乘：

res
res[0]	1	num[1]	…	num[n-2]	num[n-1]
res[1]	num[0]	1	…	num[n-2]	num[n-1]
…	…	…	…	num[n-2]	num[n-1]
res[n-2]	num[0]	num[1]	…	1	num[n-1]
res[n-1]	num[0]	num[1]	…	num[n-2]	1

代码为：

class Solution:
    def productExceptSelf(self, nums: [int]) -> [int]:
        res, p, q = [1], 1, 1
        for i in range(len(nums) - 1): # top triangle
            p *= nums[i]
            res.append(p)
        for i in range(len(nums) - 1, 0, -1): # bottom triangle
            q *= nums[i]
            res[i - 1] *= q
        return res