图论：tarjan算法

• 可以求有向图强连通分量个数，每个强连通分量的节点数等，还可以求割点和桥
• 强连通图G：G中任意两节点都可以相互到达
• 强连通分量：G不是强连通图，但G的子图G'是强连通图，则G'为G强连通分量。强连通分量是环。
• 割点：如果去掉图中节点v及与v相连的边后，图的强连通分量变多了，则v为割点
• 桥：如果去掉某条边后图的强连通分量变多了，则该条边为桥。
• 有割点不一定有桥，有桥一定有割点。如C为割点，但与C相连的边都不是桥。

Tarjan 割点判断

tarjan算法是对DFS的优化，在dfs时割点的依据：

1. 如果一个节点是根节点，则如它的子节点数>1,则它为割点
2. 如果不是根节点，设为u,则若它的子节点中有一个节点v不能到达u的祖先节点，则u为割点。

Tarjan求强连通分量

1. dfn[] 数组：DFN[u]为节点 u 搜索的次序编号；可用来判断节点u是否被搜到过。
2. low[] 数组：表示该点能直接或间接到达时间最小的顶点。例如：low[u]为节点 u 或其子树能够追溯到最早的栈中节点的次序号；
3. stack 存储该连通子图中的所有点
4. scnt:存强连通分量个数
5. scc[]:记录每个节点属于的强连通分量编号

如： 

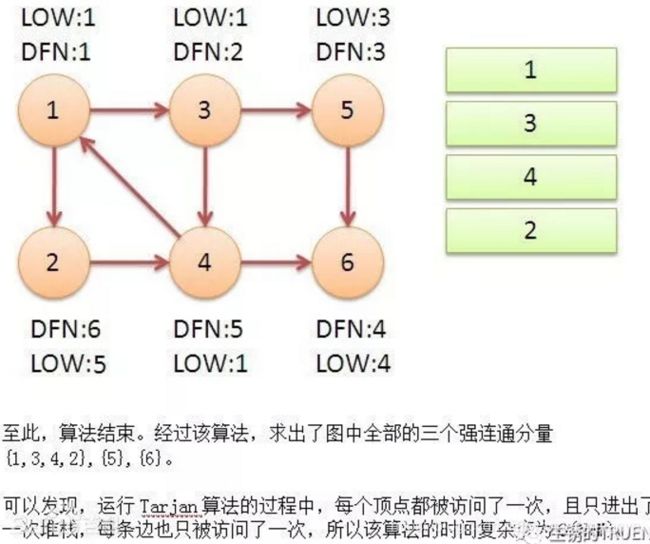
（1）从1开始DFS搜到6，其中经过3,5,都入了栈。由于6没孩子节点，所以循环结束，判断得dfn[6]==low[6]，因为6就在栈顶，所以6单独作为一个强连通分量。

（3）从6回溯到5，同6一样，再没子节点了，出栈，单独作为一个强连通分量。

（3）回溯到3后，3继续搜到4,4搜到6，已搜过且不在栈中，再搜到1,1在栈中，更新low[4]=1,dfn[4]!=low[4],回溯到3.

（4）从4回溯到3后，3更新low[3]=low[4]=1。dfn[3]!=low[3],回溯到1.

（5）从3回溯到1后，1更新low[1]=low[3]=1。1继续搜到2,2搜到4发现4已经搜过且在栈中，更新low[2]=dfn[4]=5;回溯到1.

（6）dfn[1]==low[1],2,4,3,1依次出栈，构成强连通分量。

 

【NOIP2015】信息传递

theme:n个人传信息，指定每个人可以把信息传给谁(每个人可以从多个人那里获得信息，但只能将信息传给一个人)。开始时每个人只知道自己的生日，每经过一轮游戏将当前知道的信息告诉对应的人，问最少经过几轮有人听到了自己的生日信息？

solution：即求最小环中元素的个数，也就是最小强连通分量节点个数。

//求强连通分量中最小的节点个数
#include
#include
#include
using namespace std;

const int SIZE=1000010;
int index,ans;
vectorE[SIZE];
stacks;
int dfn[SIZE];
int low[SIZE];
bool exist[SIZE];//是否还在栈内

void initT(int n)
{
    fill(dfn,dfn+n+1,0);
    fill(low,low+n+1,0);
    fill(exist,exist+n+1,false);
    index=0;
    ans=n;
}

void mkEdge(int n)
{
    for(int i=1;i<=n;++i)
    {
        int a;
        cin>>a;
        E[i].push_back(a);
    }
}

void tarjan(int u)
{
    dfn[u]=low[u]=++index;
    s.push(u);
    exist[u]=true;
    for(int i=0;i1)
            ans=min(ans,cnt);
    }
}

int main()
{
    int n;
    while(cin>>n&&n)
    {
        initT(n);
        mkEdge(n);
        for(int i=1;i<=n;++i)
            if(!dfn[i])
                tarjan(i);//如果执行多次说明原图不连通
        cout<

判断割点

poj3713：Transferring Sylla

theme:给定一个无向图，判断是否每两个点间都有3条独立路径，独立路径即只共起点和终点。

solution：枚举每个点，判断删掉后图中是否有割点，如果有，则说明不是三连通图。

#include 
#include 
#include 
#include 

using namespace std;

int del, root;
bool cut;
int dfn[510], low[510];

vector e[510];
int n, m;
int tot;

void Tarjan(int u, int p) { // 当前节点，父亲节点
    if (cut) return;
    dfn[u] = low[u] = ++tot;
    int son = 0;
    for (vector::iterator it = e[u].begin(); it != e[u].end(); ++it) {
        int v = *it;
        if (v == p || v == del) continue;
        if (!dfn[v]) {
            ++son;
            Tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if ((u == root && son > 1) || (u != root && low[v] >= dfn[u])) { // 割点条件
                cut = 1;
                return;
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }

}

int main() {
    while (scanf("%d%d", &n, &m) != EOF && n) {
        for (int i = 0; i < n; ++i) e[i].clear();
        for (int i = 0; i < m; ++i) {
            int u, v;
            scanf("%d%d", &u, &v);
            e[u].push_back(v);
            e[v].push_back(u);
        }
        cut = 0;
        for (int i = 0; i < n; ++i) {
            del = i;
            memset(dfn, 0, sizeof(dfn));
            tot = 0;
            root = !i;

            Tarjan(root, -1);
            if (cut) break;
            for (int j = 0; j < n; ++j) {
                if (j != del && !dfn[j]) {  // 不是连通图
                    cut = 1;
                    break;
                }
            }
            if (cut) break;
        }
        printf("%s\n", cut ? "NO" : "YES");
    }
    return 0;
}