菜是原罪der惹某第13周周记(习题+感悟)
蒟蒻周
- (一)2019 ICPC Asia Xuzhou Regional
- A - < 3 numbers
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B - Cat
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C - The Answer to the Ultimate Question of Life, The Universe, and Everything.
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (二)2019 ICPC Asia Nanchang Regional
- A - And and Pair
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B - Who is the Champion
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C - Bob's Problem
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- D - Eating Plan
- 题目描述
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (三)我的感想(略略略)
- 关于这周的日常练习
(一)2019 ICPC Asia Xuzhou Regional
A - < 3 numbers
题目描述
Rosie likes to play with positive integers, especially the < 3 numbers in positive integers.
< 3 number is a special group of positive integers, all of which can be divided by less than three positive integers.
For example, 7 is a < 3 number. There are two positive integers that divide 7 by 1 and 7. 25 is not a number less than 3. There are 1, 5 and 25 that can divide 25.
Now, Rosie is curious about how many < 3 numbers are included between positive integers L and R. But it’s too difficult to figure out exactly how many < 3 numbers there are. Rosie wants to know whether the proportion of < 3 numbers between L and R is less than one third. To be exact, if there are x < 3 numbers between L and R, Rosie wants to know if x / (R−L+1) < 1/3 .
Please help the curious Rosie to answer his questions.
Input
The first line has a positive integer of T, which represents the total number of test data.
Each test data is a line of two integers L, R.
· 1 ≤ T ≤ 100
· 1 ≤ L ≤ R ≤ 1e9
Output
Please output one line for each test data. If the proportion of < 3 numbers between L and R is less than one third, output Yes, otherwise output No.
Sample Input
3
7 7
25 25
5 14
Sample Output
No
Yes
No
理解
这题原本上手的时候卡了一下,然后李妍薇大佬说素数的分布是越来越稀疏的
然后暴力打表打了几个找了一下规律
然后这题有需要注意的是1也是满足条件的
然后可以发现左右区间大小大于50的时候一定是 < 1/3 的,所以直接输出Yes
当区间小于50 的时候,暴力跑一遍不会超时,直接判断就完事了
AC代码
#includeB - Cat
题目描述
Yen-Jen loves cat very much.
Now, there are 1e18 cats standing in a line, the i-th cat’s cost value ci is equal to i, the i-th cat’s index is also equal to i.
Now, Yen-Jen wants to buy some cats with continuous index, but he only has S dollars. He wants to buy some cats with continuous indices. In order to buy cat with index x, x + 1,…, y - 1, y, he needs to spend x⊕(x+1)⊕⋯⊕(y−1)⊕y dollars. ⊕ is the bitwise exclusive-or operator.
Now, he wants to ask you T questions. In each question, he has S dollars, and he wants the indices of cats in range [L, R]. What’s the maximum number of cat that Yen-Jen can buy? If he can’t buy any cat, please report -1 instead.
Input
The first line of the input file contains one integer T denotes the number of questions that Yen-Jen wants to challenge you.
Then, in the next T lines, each line contains one question. In each line, there are three integers L, R, S, which means that Yen-Jen has S dollars, and he wants to buy cats whose indices are in the range [L, R].
·1 ≤ T ≤ 5×1e5
·1 ≤ L ≤ R ≤ 1e18
·0 ≤ S ≤ 2×1e18
Output
In each question, output the maximum number of cats that Yen-Jen can buy. If Yen-Jen can’t buy any cats, output -1 instead.
Sample Input
2
1 1 0
2 2 2
Sample Output
-1
1
理解
起先根据异或自己试了 0^1 1^2 3^4 几组 然后发现 2^3^4^5 == 0 然后错以为 四个相连都是为 0
然后发现只有结尾是奇数才能实现 四个连续的数字异或为 0
那么就可以简单地处理一下 这一串连续的数字
因为题目要求连续的取 所以先判断一下最后一个是奇数还是偶数
如果是奇数就往前4个4个的取,肯定异或完都是0,
然后在判断前面剩下的最多能取几个就好了
如果是偶数 就先不取最后一个 然后从倒数第二个开始往前4个4个取都异或为 0
然后剩下 < 4 的个数直接暴力判断
WA了很多发,怪我代码码的太乱了,后来还是找错误样例才发现了很多漏洞
这个码字能力是我太弱了(嘤嘤嘤)
AC代码
#includeC - The Answer to the Ultimate Question of Life, The Universe, and Everything.
题目描述
For decades, scientists have wondered whether each of the numbers from 0 to 100 could be represented as the sum of three cubes, where a cube is the same number multiplied together three times.
42 was the last number without a proven solution — until now.
The solution is (-80538738812075974)^3 + (80435758145817515)^3 + (12602123297335631)^3 = 42
Now, Yen-Jen is suspicious of the existence of other solutions. But, the solutions are not so trivial to find out. Yen-Jen wants to find out easysolutions first. That is, for the equation a^3 + b^3 + c^3 = x,Yen-Jen wants to find out at least one solution for each integer x in [0, 200],where ∣a∣,∣b∣,∣c∣≤5000.
Since Yen-Jen is still busy preparing the test data of some(this?) problem, pleasehelp him find out at least one solution for each xx or tell him that thesolution doesn’t exist when∣a∣,∣b∣,∣c∣≤5000.
Input
The first line contains an integer T indicating the number of x to bechecked.Following T lines each contains one integer x.
·1 ≤ T ≤ 10
·0 ≤ x ≤ 200
Output
For each test case, output one line containing three space-separated integers a, b, ca,b,c such that a^3 + b^3 + c^3 = x and ∣a∣,∣b∣,∣c∣≤5000. If thesolution doesn’t exist, output impossible.
Sample Input
2
1
2
Sample Output
1 1 -1
1 1 0
理解
这道题,其实我理解了题意后并没有什么想法
优秀的张李彬同学和他的小伙伴们,暴力打表了(足够优秀昂)
AC代码
#include(二)2019 ICPC Asia Nanchang Regional
A - And and Pair
题目描述
Given an extremely large non-negative integer nn, you are asked to count the number of pairs (i,j) of integers satisfying the following conditions:
0 ≤ j ≤ i ≤ n;
i & n = i; and
i & j = 0.
Here & represents the bitwise AND operator.
For simplicity, the binary representation of n will be given. Meanwhile, you only need to output the answer modulo (10^9+7).
Input
The first line contains an integer T (1 ≤ T ≤ 20) indicating the number of test cases.
Each of the following T lines contains a string S (1 ≤ ∣S∣ ≤ 1e5) which is the binary representation of the non-negative integer nn. Note that leading zeros of S could appear in the input.
Output
For each test case, output a line containing the answer described above modulo (10^9+7).
Sample Input
2
111
1010
Sample Output
14
15
理解
起先卡在了找规律上,三个人埋头苦想了一年的规律
果然还是先暴力打一遍找规律昂
然后最先发现的是,通过 i 去推 j 的时候,只要看 每个 i 最高 1 位后有几个 0 就有2的几次方个 j
然后 i 的规律 是看 n 的二进制里 每位的 0 必定对应 0,而 1 位可以对应0/1 但是不同的 i 和 j 对应就毫无头绪
然后我和张李彬去开了 L题,优秀的思维大佬(李妍薇)在静想了一会后 发现了总个数的规律
是看每一位后面的1和0的个数来相加的,每次* (2 的 num0次 + 3 的 num1 次)
然后值得注意的是当数量为 0 的时候不在计入
所以只需要跑一遍字符串记录0 1 个数
然后从头往后推 每次 遇到 1 就 * 一遍上面的公式 ,然后 num1-- ,遇到 0 就num0--;
wa了一发小细节(嘤嘤嘤)
AC代码
#includeB - Who is the Champion
题目描述
Soccer is probably the sport with the greatest fans in this country. However, the national team has a poor record on the world stage. In order to energize youth players, the Soccer National Championship is organized every year.
In this year, there are nn teams taking part in the championship. As usual, the single round-robin system is adopted so that each team plays every other team once. A standard match askes ten players and a goalkeeper for both teams, which contains 22 players in total. They confront each other, defend their nets and attack the opponent’s goal in a rectangular grass court.
In a 90-minute game, they try to shoot again and again. When the game is over, the team with higher goals will win and obtain 3 points in the scoreboard, while the loser will obtain nothing. A very special but common case is that both teams get the same goals, which is a draw; then both of them will obtain one point in the scoreboard.
At the end of the season, the league will declare the champion which is the team with the highest score in total. If two or more teams have the same highest score in total, the one with the highest goal differential (which is calculated as the number of goals scored in all league matches minus the number of goals conceded) will be the champion. The worst situation that several teams have the same highest score in total and the same goal differential will be solved by extra play-offs.
Input
The first line contains an integer n (1 ≤ n ≤ 100) indicating the number of teams.
Each of the following nn lines contains nn integers.The j-th integer in the i-th line, which is non-negative and up to five, represents the number of goals scored by the i-th team against the j-th team.
We guarantee that a(i,i)=0 for all 1 ≤ i ≤ n.
Output
If the league can declare the champion, output the index of the team who will be the champion or output play-offs (without quotes), if extra play-offs will be organized.
Sample Input
样例输入1
2
0 1
2 0
样例输入2
2
0 1
1 0
样例输入3
3
0 1 3
1 0 4
0 0 0
Sample Output
样例输出1
2
样例输出2
play-offs
样例输出3
2
理解
这题讲了一堆废话,就是平局两者各记+1分,不是平局就赢家+3分
然后如果出现总分一样就记录这些球队总的进球数和输球数
然后只需要在输入后开三个数组,一个记录总分,一个记录进球总数,一个输球总数
起先wa一发是。。。莫名其妙自己sort了一下,,,是我太傻了
就是一道暴力题,小问题
AC代码
#includeC - Bob’s Problem
题目描述
Bob was in trouble.He rubbed the magic ring on his finger, and you came out of the ground.
You are given an undirected graph G which contains nn vertices labelled from 1 to n, with mm weighted edges between them coloured in black or white.You have to choose some edges in G such that there is at least one path between any two vertices only passing by selected edges, and you can select no more than k white edges.There may be multiple available strategies to determine these edges, and you are asked to find out the way with a maximum total weight of edges.
Input
The first line contains an integer T (1 ≤ T ≤ 5) indicating the number of test cases.
For each test case, the first line contains three integers n (1 ≤ n ≤ 50000), m and k (1 ≤ k ≤ m ≤ 500000).
Each of the following mm lines contains four integers u, v (1 ≤ u,v ≤ n),w (0 ≤ w ≤ 100000) and c (0 ≤ c ≤ 1) describing an edge of weight ww and colour cc between the u-th vertex and the v-th vertex. Here an edge is white if c = 1, or black if c = 0.
Note that there may be multiple edges between some vertices, and self-loops are also allowed.
Output
For each test case, output a single line with an integer indicating the maximum total weight of selected edges, or output -1 if there is no solution for the given graph.
Sample Input
1
5 6 2
1 2 0 0
1 3 5 1
1 5 1 0
2 3 6 1
2 4 2 0
3 4 7 1
Sample Output
16
理解
再夸一波图论小能手张李彬同学
首先看完题意推了一波 发现只限制了白边条数
所以黑边是一定会加上的
然后要求连通每个点
此时再去对白边的增加做判断即可
wa两发的原因是没开 long long 嘤嘤嘤
AC代码
#includeD - Eating Plan
题目描述
Bob is hungry now and he needs to eat some food. Alice puts nn dishes of food in front of him, numbered from 1 to n. Alice tells him that he can only eat continuous dishes of food, or he will be poisoned by food. For example, if there are 10 dishes, he can eat the food in the 2-nd, 3-rd and 4-th dishes but he can not eat the food in the 2-nd, 3-rd and 5-th dishes because there is the 4-th dish between them so it’s not continuous. Furthermore, if he chooses to eat food in the ii-th dish, he has to eat all food in that dish.
Bob’s stomach has a strange feature that if there is at least t (=998857459) kg food in it, the weight in it will reduce t kg repeatedly until it is strictly lower than tt kg. Also, if the weight of food in his stomach is exactly t kg, his stomach will be empty. Now Bob wants to eat the smallest number of dishes and remains no less than k kg food in his stomach. Can you tell him how many dishes he needs to choose?
Input
The first line contains two integers nn and m~(1\leq n\leq 100000,1\leq m\leq 10000)m (1 ≤ n ≤ 100000,1 ≤ m ≤ 10000), indicates the number of dishes and the number of queries.
The second line contains n integers a1,a2,⋯,an, which is a permutation of 1,2,⋯,n, indicates that there is (ai!) kg food in the ii-th dish, where s! = 1×2×3×⋯×s.
The third line contains mm integers, the i-th integer ki(1 ≤ ki < t) indicates a query with the lower bound of weight.
Output
Each line of mm lines contains an integer indicates the number of dishes Bob needs to choose in that query. If there is no way to reach Bob’s target, output -1 instead.
Sample Input
4 2
1 2 3 4
29 31
Sample Output
2
3
理解
在此一定要吹一波紫妈(某陈姓大佬)最后几分钟A了,也太强了
代码不是我码的,后来还找他帮我分析了一波题目思路(我吹爆)
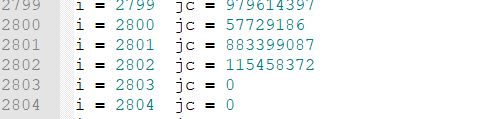
首先根据题意 暴力打表 数字的阶乘 然后对 t 取模 找了一波规律 然后发现 到2802
刚好 % 2803 == 0 然后后面都是 0 了
然后只需要打表打到3000(保险起见)
然后记录输入的每个点的下标和值
然后用一个n^2的循环来枚举每一个区间,记录下每一个区间的下标和长度,以及大小
然后进行一次排序 先根据 值从小到大 然后根据长度从小到大
然后暴力循环 直到找到第一个区间 的值比询问的k大
从这个区间往后都是满足条件的
然后用一个线段树 维护一个最小区间
就可以得到答案啦!
AC代码
#include (三)我的感想(略略略)
关于这周的日常练习
这两次的徐州和南昌重现赛感觉配合略好些了,一个人思考的时候,另外两个人开新题,
毕竟有很多签到题(误)然后就分工合作
真的很躺赢,毕竟有一个思维大佬和一个图论大佬带我,嘤嘤嘤
这周的dp专题也没有好好的刷起来,刷题速度太慢了,,,
然后感觉离西安的时间越来越近了,一边紧张一边划水(误)应该是一边学习!
不会的东西好多 学不完啦,不过没关系,学到就是赚到 over
以及今天写博客的时候发现一个很骚的操作
如下:如何在CSDN上搞花里胡哨的爱心(嘻嘻)
❤️ ❤️ ❤️ ❤️ ❤️ ❤️