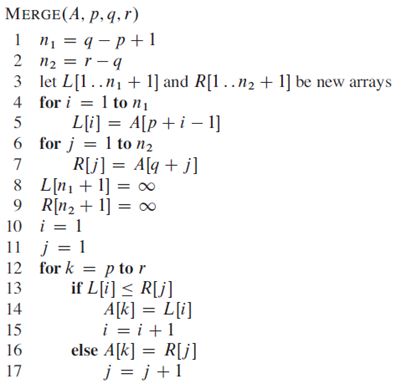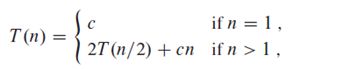1. 循环不变式
循环不变式帮助我们理解算法正确性。利用循环不变式时,需要证明以下三条性质。
初始化:循环第一次迭代前,循环不变式为真.(对应归纳法中的基本情况)
保持:如果循环在某次迭代前为真,则在下次迭代之前也为真。(对应于归纳步)
终止:循环终止时,不变式提供一个有用的性质,该性质有助于证明算法的正确性。(与归纳区别,归纳法中归纳步无限使用,而此处会终止)
2. 插入排序(Insertion Sort)
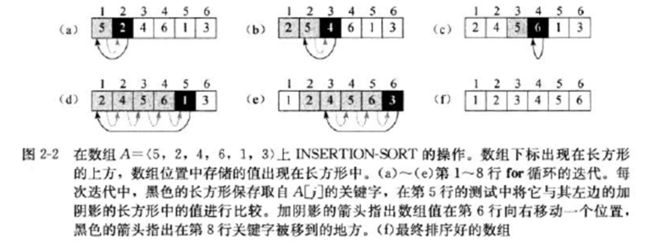
插入排序是最基本的排序算法,其方法概括为:从数组的第2个元素开始向后遍历数组,对每个元素A[j]先存于key中,然后从j开始向前查找,如果之前的元素x比key大则将该元素后移一位,直到查找到第1个元素或者元素x的值<=key,则将key存于该元素x的位置。伪代码如下:
对一个数组A={5,2,4,6,1,3}的插入排序过程说明如下:
时间复杂度分析:最好情况(即数组已经排序好)an+b,最差情况(即数组逆序排列)an^2+bn+c,所以插入排序的最坏运行时间为Θ(n^2)。
3. 归并排序(Merge Sort)
3.1 分治法
递归算法结构:在解决一个问题是,算法一次或者多次调用自身来解决紧密相关的若干个子问题。
分治法思想:把原问题分解为若干个相似的子问题,递归求解子问题,然后合并这些子问题的解得到原问题的解。
分治模式在每层递归中的三步骤:
1)分解:将原问题分解为若干个子问题,子问题是原问题规模较小的实例。
2)解决:对于每个子问题递归求解,如果子问题规模足够小时则直接求解。
3)合并:合并若干个子问题的解得到最终原问题的解。
3.2 归并排序
3.2.1 步骤
完全遵循了分治模式的三步骤:
1)分解:分解待排序的长为n的序列为两个2/n的子序列。
2)解决:使用归并排序递归地排序两个子序列。
3)合并:合并两个已排序的子序列生成原问题的解。
3.2.2 合并函数(MERGE)
归并排序中的关键步骤是一个子函数MERGE,负责对两个已经各自排序子序列进行按序合并。
其总体思想是:对两个子序列比较它们各自最小的元素,谁小就放到存放结果的数组(假设为A)中,当某个子序列空了,则可以在其最后一位设一个无穷大的哨兵,使得另为一个数组的第一位肯定小于该哨兵,则能顺利把未空子序列剩余的元素放到A中,完成合并。
其伪代码如下:
输入参数为待排数组A,合并的序列头p,中间某个位置的标识q,序列尾r。第1-3行得到两个分拆子序列的各自长度,并且定义左右子序列分别为L和R。4-7行将数组A中的元素拷贝到L和R中。8-9行设立两个哨兵位,并另为无穷大。10,11行设立扫描L和R的index初值,12-17为核心循环,k为A的p-r段的扫描index,每次循环都比较L和R的第一个元素的大小,小的放入A中k指的位置,并且该索引i或j自增1以保证循环不变式的保持。时间复杂度由12-17行决定,为Θ(n)。
以下例子可以很好地帮助理解:
3.2.3 排序函数(MERGE-SORT)
归并排序递归地划分序列并解决子序列的排序,直到子序列只剩一个元素时不再递归划分(不可分),这个时候会一次向上执行合并步骤,直到得到最终排序数组。
伪代码如下:
第一个判断语句表明p如果≥r则表示只有一个元素,不再递归,初次调用时,p为1,r为A.length。
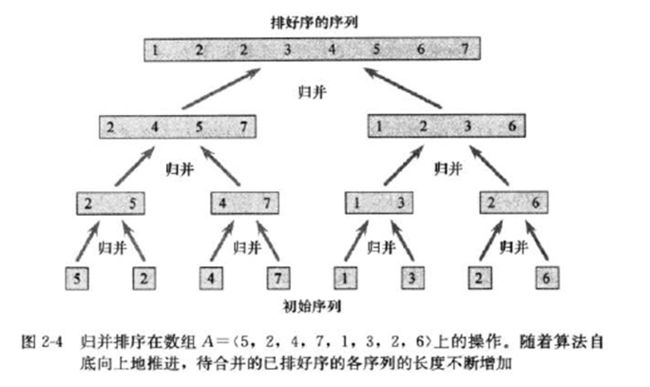
一个长度为8的序列归并排序过程如下:
3.2.4 时间复杂度分析
对于一个递归问题,往往可以用递归方程或者递归式来描述运行时间。如下:
当问题规模足够小,则时间为Θ(1),否则,在三步骤的解决中将规模为n的问题拆为a个每个规模为原来的1/b的问题时,耗时为aT(n/b),假设分解步骤需要时间为D(n),合并时间为C(n)则可得上式。
对于归并排序,上式中解决步骤即为将规模为n的问题分解为2个规模为原问题1/2的子问题,分解耗时为常数时间Θ(1),合并为Θ(n)。所以耗时T(n)如下:
其中,c为常数。
我们可以用递归数方便地求得其时间复杂度量级:
关键点为,由树高和每层的分子的关系求得递归数的树高,进而得到树的层数求得复杂度为Θ(nlgn)。
原创博客,转载请注明:http://www.cnblogs.com/wuwenyan/p/4945559.html