最短路径算法--无向图
最短路径算法
Dijkstra算法是最短路径算法中为人熟知的一种,是单起点全路径算法。该算法被称为是“贪心算法”的成功典范。
1、表示图的数据结构
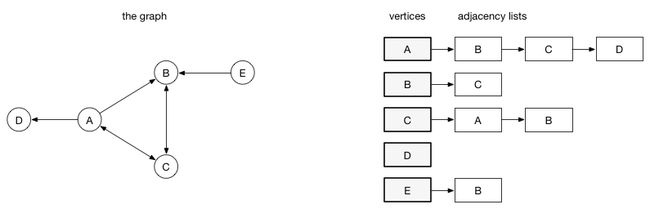
邻接列表
邻接列表:在邻接列表实现中,每一个顶点会存储一个从它这里开始的边的列表。比如,如果顶点A 有一条边到B、C和D,那么A的列表中会有3条边
邻接列表只描述了指向外部的边。A 有一条边到B,但是B没有边到A,所以 A没有出现在B的邻接列表中。查找两个顶点之间的边或者权重会比较费时,因为遍历邻接列表直到找到为止。
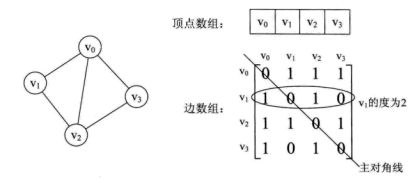
邻接矩阵
邻接矩阵:在邻接矩阵实现中,由行和列都表示顶点,由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如,如果从顶点A到顶点B有一条权重为 5.6 的边,那么矩阵中第A行第B列的位置的元素值应该是5.6:
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
(1)要判断任意两顶点是否有边无边就很容易了;
(2)要知道某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
(3)求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点;
而有向图讲究入度和出度,顶点vi的入度为1,正好是第i列各数之和。顶点vi的出度为2,即第i行的各数之和。
2 算法实现思路
无向图的最短路径实现相对于带权的有向图最短路径实现要简单得多。
源点的最短路径距离为0,从源点开始,采用广度优先的顺序,首先将与源点邻接的顶点的路径求出,然后再依次求解图中其他顶点的最短路径。
由于顶点的最短路径的求解顺序 是一个 广度优先的顺序,因此需要一个辅助队列。初始时,将源点的最短路径距离设置为0,将源点入队列。
然后,在一个while循环中,从队列中弹出顶点,遍历该顶点的邻接点,若该邻接点的距离未被更新过(表示该邻接点未被访问过),更新邻接点的最短路径距离为 该顶点的距离加上1,并将所有的邻接点入队列。
该算法的实现与 二叉树的层序遍历,有向图的拓扑排序算法实现都非常的相似。他们都采用了广度的思想在里面。
广度优先的思想就是:处理完某个顶点后,去处理该顶点的所有邻接点,处理完它的邻接点后,再去处理更远(更外层)的顶点。
算法的代码如下:
/*
* 计算源点s到无向图中各个顶点的最短路径
* 需要一个队列来保存图中的顶点,初始时,源点入队列,然后以广度的形式向外扩散求解其他顶点的最短路径
*/
private void unweightedShortestPath(Vertex s){
//初始化
Queue queue = new LinkedList<>();
s.dist = 0;
queue.offer(s);//将源点dist设置为0并入队列
while(!queue.isEmpty()){
Vertex v = queue.poll();
for (Edge e : v.adjEdges) {//扫描v的邻接边(点)
if(e.endVertex.dist == Integer.MAX_VALUE){//如果这个顶点(e.endVertex)未被访问(每个顶点只会入队列一次)
e.endVertex.dist = v.dist + 1;//更新该顶点到源点的距离
queue.offer(e.endVertex);
e.endVertex.preNode = v;//设置该顶点的前驱顶点
}//end if
}//end for
}//end while
} 完整代码实现
import java.util.Collection;
import java.util.LinkedHashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;
/*
* 求解无向图的单源最短路径
*/
public class NonDirectedGraph {
private class Vertex{
private String vertexLabel;//顶点标识
private List adjEdges;//与该顶点邻接的边(点)
private int dist;//顶点距离(该顶点到起始顶点的距离)
private Vertex preNode;
public Vertex(String vertexLabel) {
this.vertexLabel = vertexLabel;
adjEdges = new LinkedList<>();
dist = Integer.MAX_VALUE;
preNode = null;
}
}
private class Edge{
private Vertex endVertex;
public Edge(Vertex endVertex) {
this.endVertex = endVertex;
}
}
private Map nonDirectedGraph;//保存了图中所有的顶点,边的关系以List形式保存在Vertex类中
private Vertex startVertex;//图的起始顶点
public NonDirectedGraph(String graphContent) {
nonDirectedGraph = new LinkedHashMap<>();
buildGraph(graphContent);
}
private void buildGraph(String graphContent){
String[] lines = graphContent.split("\n");
String startNodeLabel, endNodeLabel;
Vertex startNode, endNode;
for(int i = 0; i < lines.length; i++){
String[] nodesInfo = lines[i].split(",");
startNodeLabel = nodesInfo[1];
endNodeLabel = nodesInfo[2];
endNode = nonDirectedGraph.get(endNodeLabel);
if(endNode == null){
endNode = new Vertex(endNodeLabel);
nonDirectedGraph.put(endNodeLabel, endNode);
}
startNode = nonDirectedGraph.get(startNodeLabel);
if(startNode == null){
startNode = new Vertex(startNodeLabel);
nonDirectedGraph.put(startNodeLabel, startNode);
}
Edge e = new Edge(endNode);
//对于无向图而言,起点和终点都要添加边
endNode.adjEdges.add(e);
startNode.adjEdges.add(e);
}
startVertex = nonDirectedGraph.get(lines[0].split(",")[1]);//总是以文件中第一行第二列的那个标识顶点作为源点
}
public void unweightedShortestPath(){
unweightedShortestPath(startVertex);
}
/*
* 计算源点s到无向图中各个顶点的最短路径
* 需要一个队列来保存图中的顶点,初始时,源点入队列,然后以广度的形式向外扩散求解其他顶点的最短路径
*/
private void unweightedShortestPath(Vertex s){
//初始化
Queue queue = new LinkedList<>();
s.dist = 0;
queue.offer(s);//将源点dist设置为0并入队列
while(!queue.isEmpty()){
Vertex v = queue.poll();
for (Edge e : v.adjEdges) {//扫描v的邻接边(点)
if(e.endVertex.dist == Integer.MAX_VALUE){//如果这个顶点(e.endVertex)未被访问(每个顶点只会入队列一次)
e.endVertex.dist = v.dist + 1;//更新该顶点到源点的距离
queue.offer(e.endVertex);
e.endVertex.preNode = v;//设置该顶点的前驱顶点
}//end if
}//end for
}//end while
}
//打印图中所有顶点到源点的距离及路径
public void showDistance(){
Collection vertexs = nonDirectedGraph.values();
for (Vertex vertex : vertexs) {
System.out.print(vertex.vertexLabel + "<--");
Vertex tmpPreNode = vertex.preNode;
while(tmpPreNode != null){
System.out.print(tmpPreNode.vertexLabel + "<--");
tmpPreNode = tmpPreNode.preNode;
}
System.out.println("distance=" + vertex.dist);
}
}
} 图理解
参考链接
https://blog.csdn.net/yu121380/article/details/79810233
![]()
对于求最短路径的问题一般都会给出一幅图,或者边与边的关系。如上图。
假设我们起点是A,我们要求到F的最短距离,我们会怎么做?
首先,因为A是起点,所以我们把对于每个点都有个参数,相对于A的距离,默认除了A到A为0,其他都是无穷大。
![]()
从起点A开始,我们更新与A相连通的点到A的距离,并把A点标记。如图: ![]()
我们遍历一次所有点与A的距离,找到最小的,这里是点B。
以它为起点,把它周围未被标记的点拿来做比较,显然,像F这种没有与A练过的点,当前距离就会变成min(dis[B]+maze[B][F],INF),就是B到起点的距离加上BF之间的距离。而像c这种与A直接相连的点,当前距离就会变成min(dis[B]+maze[B][C],dis[c]),所以按照我们每次只需要比较当前点到当前状态起点的和与当前点到起点的距离就可以了。 ![]()
然后我们遍历发现,当前未被标记且到起点距离最小点的点是C点。我们更新连接了C的所有点。同样利用上面的min公式。
![]()
同理,更新D点的邻点。
![]()
再把更新E点的邻点。
![]()
最后再更新F点。发现F点周围所有点都被标记了,不做更新。
再遍历,发现图中所有点都被遍历了,算法结束。
这个时候,我们已经求出了所有点到起点的最小距离。
可以直接输出dis[F]求得A到F的最短路径。
注意:
上面的图重点是看每次变化找的起点和与出发点路径的变化。
当前起点是当前未被标记且到出发点距离最近的点。
更新的点都是与该起点直接相连并未被标记的点。
因为并没有无穷大这个数,所以我们把INF设为一个我们计算不能到达的数,这里的数接近int的上限,可以近似看作正无穷。
————————————————
#include"iostream"
#include"cstring"
#include"cstdio"
using namespace std;
#define INF 0x7f7f7f7f
const int N = 105; //点的个数上限
int maze[N][N];
int dis[N];
bool vis[N];
//点的个数和边的条数
int n,m;
void init()
{
memset(maze,INF,sizeof(maze));
memset(dis,INF,sizeof(dis));
memset(vis,false,sizeof(vis));
}
void dijkstra(int st)
{
dis[st]=0;
for(int i=1; i<=n; i++)
{
//找到和起点距离最短的点
int minx=INF;
int minmark;
for(int j=1; j<=n; j++)
{
if(vis[j]==false&&dis[j]<=minx)
{
minx=dis[j];
minmark=j;
}
}
//并标记
vis[minmark]=true;
//更新所有和它连接的点的距离
for(int j=1; j<=n; j++)
{
if(vis[j]==false&&dis[j]>dis[minmark]+maze[minmark][j])
dis[j]=dis[minmark]+maze[minmark][j];
}
}
}
int main()
{
while(scanf("%d %d",&n,&m)!=EOF)
{
if(n==0&&m==0) break;
//每组数据都要初始化
init();
for(int i=1; i<=m; i++)
{
int x,y,len;
scanf("%d %d %d",&x,&y,&len);
if(x!=y&&maze[x][y]>len)
{
maze[y][x]=len;
maze[x][y]=len;
}
}
//以1为起点跑一次dij
dijkstra(1);
//输出到n的距离
printf("%d\n",dis[n]);
}
}